Leetcode 37 解数独-编程知识

Leetcode 37 解数独

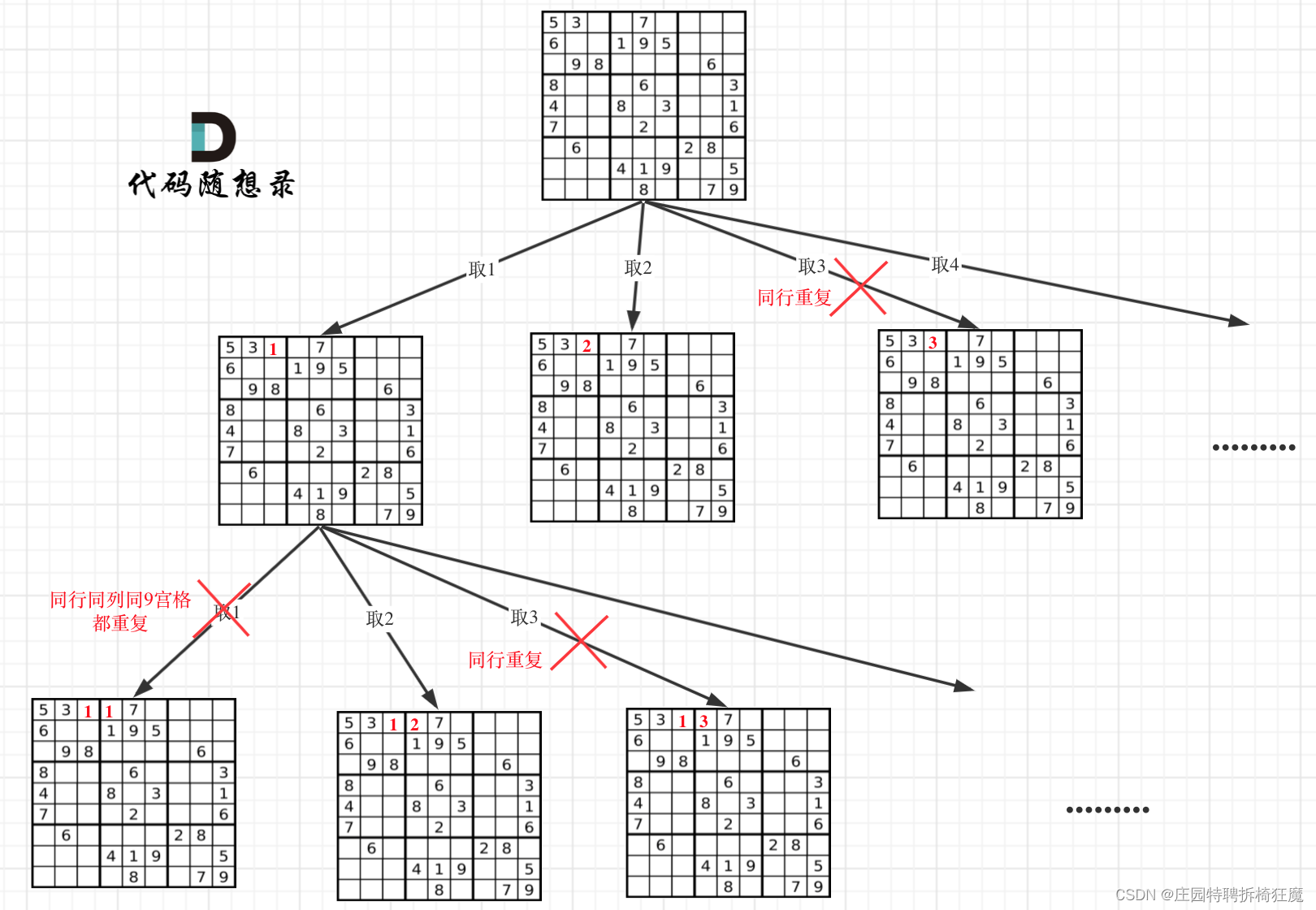
题意理解：

填充数独。每个九宫格内，9个数字各出现一个次，每行，每列上，9个数字各出现一次。数独部分空格内已填入了数字，空白格用 '.' 表示。

这道题要比N皇后问题更难：

N皇后只放置N个皇后的位置，但是数独需要填满整个结构。

N皇后每个位置只有放与不放两种状态，但是数独每个位置都有1-9个选择。

所以我们不止要遍历数独上的每个位置，还要遍历1-9的数字，以保证在合适的位置放上合适的数字。



图摘自《代码随想录》

解题思路：

N皇后、数独问题，都可以使用回溯法来解决。

        其实都是可以将问题解决看作一个一个步骤，前一个步骤会对后一个步骤产生影响，且每个步骤都有n个选择。这是一大类问题。

所以仍旧可以将其解决方案抽象为一个树结构。



图摘自《代码随想录》

1.暴力回溯+剪枝优化

前提条件：判断该位置填某数字是否合法

这与寻找N皇后合法的摆放位置不同，我们只要求得将数独填完得唯一解即可，所以这里我们用到的回溯方法可以设置返回值。

第一个for循环遍历每一行

第二个for函数相当于遍历每一个行的每一个位置。

由于每个位置又有1-9的选择，所以还需要一个for循环来控制数字选择——选择到正确值则向下递归，要么找到正确解，要么找不到。

某位置找不到正确解时，board状态向上回溯——return false。

回溯的三个步骤：确定返回值和参数列表：有返回值，指示是否能获得唯一的解。

确定终止条件：找到唯一解即终止。

确定单层递归逻辑：递归的目的是找到满足条件的唯一解。

 public void solveSudoku(char[][] board) {backtracking(board);}//回溯求唯一解public boolean backtracking(char[][] board){//终止条件，找到唯一解时即返回//遍历该行的每一个位置for(int rowIndex=0;rowIndex<board.length;rowIndex++){for(int colIndex=0;colIndex<board.length;colIndex++){//是否需要填数字if(board[rowIndex][colIndex]!='.') continue;//控制数字选择for(char num='1';num<='9';num++){//判断填入该数字是否合法if(isValid(board,rowIndex,colIndex,num)){board[rowIndex][colIndex]= num;boolean result=backtracking(board);if(result==true) return true;board[rowIndex][colIndex]= '.';}}//换了9个数字都没有return true,则额说明这样下去找不到合适解return false;}}return true;}//判断在board的（ rowIndex, colIndex）填入num是否合法public boolean isValid(char[][] board,int rowIndex,int colIndex,char num){//行判断for(int j=0;j<board.length;j++) if(board[rowIndex][j]==num) return false;//列判断for(int i=0;i<board.length;i++) if(board[i][colIndex]==num) return false;//九宫格判断int startI=Math.floorDiv(rowIndex,3)*3,startJ=Math.floorDiv(colIndex,3)*3;//九宫格左上角起始位置for(int i=0;i<9;i++){//遍历九宫格的9个位置if(board[startI+Math.floorDiv(i,3)][startJ+i%3]==num) return false;}return true;}