题目
n(n<=500)种球,第i种有ai(0<=ai<=1e12)个球,
m(m<=5e5)个盒子,第j个能放bj(0<=bj<=1e12)个球
特别地,第j个盒子最多能放i*j个第i种球
求m个盒子能放的最多的球的总数
思路来源
官方题解
题解
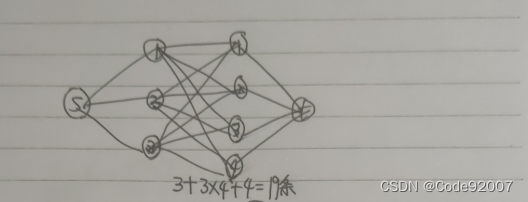
显然是一个最大流模型,超级源点s到超级汇点的流量t,
由于最小割=最大流,可以考虑最后这个图,割完之后长什么样

比如左侧1、3记为集合P含于S,右侧点2记为集合Q含于S,
那么,记左侧集合非P含于T,右侧集合非Q含于T
那么,最小割的边集的构成,由三部分组成:
1. 超级源点s与集合非P之间的边,即左侧属于t的点,断开与s的边
2. 集合Q与超级汇点t之间的边,即右侧属于s的点,断开与t的边
3. 左侧集合P与右侧集合非Q之间的边,左侧属于s的点,右侧属于t的点,断开左右点之间的边
由于边是有向的,
所以无需断开左侧属于t的点和右侧属于s的点之间的边,
因为从上游流量就已经切断了


然后就是对官方题解的一些补充说明吧,
最小割的代价由三部分组成,
形如
所以枚举,也就是左侧属于S集合的i之和,
这样可以通过dp,O(n^3)求得,
也就是属于S集合i之和固定时,不属于S集合的Ai之和的最小值
而后面两坨,k固定时,答案之和j有关,
可以任意划分,将一部分划给S集合,另一部分划给T集合,
并且划给S集合的每个点贡献是j*k,划给T集合的每个点贡献是B[j],
使得这两部分之和最小,那么考虑某一个点,自然是哪个小划给哪边,
所以每个点贡献是min(j*k,B[j])
由j*k>B[j],解得k>=B[j]/j,所以枚举k的时候,每个点从S换到T的操作只会发生一次
记录一下这个翻转的时机,即可一边枚举k一边实现对贡献的统计,
这部分复杂度O(n^2+m)
总复杂度O(n^3+n^2+m)
代码
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=505,M=5e5+10,S=N*(N+1)/2;
const ll INF=0x3f3f3f3f3f3f3f3fll;
int n,m;
ll a[N],b[M],dp[N][S],ans,sum,sum2;
vector<int>flip[S];
void upd(ll &x,ll y){x=min(x,y);
}
int main(){sci(n),sci(m);rep(i,1,n)scll(a[i]);rep(i,1,m)scll(b[i]);memset(dp,INF,sizeof dp);dp[0][0]=0;rep(i,0,n-1){int up=i*(i+1)/2,v=i+1;rep(j,0,up){upd(dp[i+1][j+v],dp[i][j]);upd(dp[i+1][j],dp[i][j]+a[i+1]);}}int lim=n*(n+1)/2;rep(j,1,m){//先认为都是j*k,再翻到b[j]ll v=b[j]/j;if(v<=lim)flip[v].pb(j);sum+=j;}ans=8e18;rep(j,0,lim){ans=min(ans,dp[n][j]+1ll*sum*j+sum2);for(auto &v:flip[j]){sum-=v;sum2+=b[v];}}printf("%lld\n",ans);return 0;
}


![[Big Bird]论文解读:Big Bird: Transformers for Longer Sequences](https://img-blog.csdnimg.cn/direct/3874e79640974bf9bf1df85a1c18262f.png)
![[计网00] 计算机网络开篇导论](https://img-blog.csdnimg.cn/direct/5406f43cd4dc444e8c89e5ce4cd49a6f.png)