435.无重叠区间

初始思路：

        我的思路就是如果有两个区间重叠，保留end比较小的那个区间，删除end比较大的区间。

class Solution {public int eraseOverlapIntervals(int[][] intervals) {Arrays.sort(intervals, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {return o1[0]-o2[0];}});int result = 0;int start = intervals[0][0];int end = intervals[0][1];for(int i = 1;i<intervals.length;i++){System.out.println("start"+start);System.out.println("end"+end);if(intervals[i][0]<end){result++;if(intervals[i][1]<end){end = intervals[i][1];start = intervals[i][0];}}else{start = intervals[i][0];end = intervals[i][1];}}return result;}
}

题解复盘：

        跟题解中按照左边排序的思路基本一致。

---

763.划分字母区间

初始思路：

以本题举例，首先是一个二维数组，统计每个字母的start和结束。

a的区间是0~8，b的区间是1~5，c的区间是4~7，d的区间是9~14，e的区间是10~15，j的区间是11，11，h的区间是16~18，i的区间是17~22，j的区间是18~23.然后类似的合并区间，

class Solution {public List<Integer> partitionLabels(String s) {List<Integer> result = new ArrayList<>();int[][] temp =  new int[26][2];for(int i = 0;i<s.length();i++){int a = s.charAt(i)-'a';if(temp[a][0]!=0){temp[a][1]=i;}else{temp[a][0] = i;temp[a][1] = i;}}int start = 0;int end = 0;Arrays.sort(temp, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {return o1[0]-o2[0];}});for (int[] ints : temp) {if(ints[1]!=0){end = ints[1];break;}}for(int i = 0;i<temp.length;i++){if(temp[i][1]!=0){System.out.println(Arrays.toString(temp[i]));if(start<=temp[i][0]&&temp[i][0]<=end){end = Math.max(end,temp[i][1]);}else{System.out.println("start"+start);System.out.println("end"+end);result.add(end-start+1);start = temp[i][0];end = temp[i][1];}}}result.add(end-start+1);return result;}
}

可以应对大多数情况，但是无法ac，对于第一个字母的处理有点奇怪。

题解复盘：

题解思路更加简洁，只关注最远的结束位置，不关注起始点。

可以分为如下两步：

• 统计每一个字符最后出现的位置
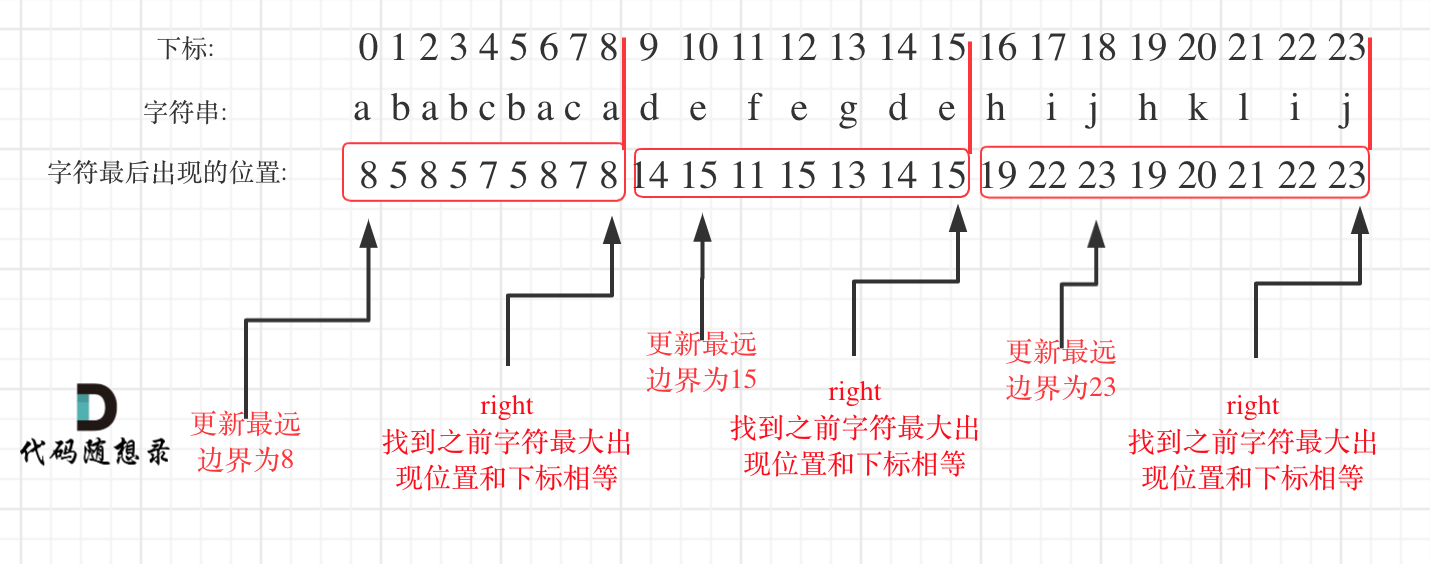
• 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

如图：

class Solution {public List<Integer> partitionLabels(String S) {List<Integer> list = new LinkedList<>();int[] edge = new int[26];char[] chars = S.toCharArray();for (int i = 0; i < chars.length; i++) {edge[chars[i] - 'a'] = i;}int idx = 0;int last = -1;for (int i = 0; i < chars.length; i++) {idx = Math.max(idx,edge[chars[i] - 'a']);if (i == idx) {list.add(i - last);last = i;}}return list;}
}

 

---

56.合并区间

初始思路：

        首先对二维数组进行排序，如果目前的左边界小于前一个的右边界则代表两个区间有重叠，那么更新区间的左边界为两个左边界之中最小的，更新右边界为两个右边界之中最大的。这可能涉及到会有三个区间重叠的情况，所以第三个区间需要和已经更新新边界的前两个区间的最终结果进行比较，从而得到新的区间，再存入的result集中。

class Solution {public int[][] merge(int[][] intervals) {if(intervals.length==1){return intervals;}Arrays.sort(intervals, new Comparator<int[]>() {@Overridepublic int compare(int[] o1, int[] o2) {return o1[0]-o2[0];}});ArrayList<int[]> al = new ArrayList<>();al.add(intervals[0]);for (int i = 1; i <intervals.length ; i = i+1) {int[] temp = al.get(al.size()-1);int a = temp[0];int b = temp[1];if(b>=intervals[i][0]){al.remove(al.size()-1);temp[0] = Math.min(a,intervals[i][0]);temp[1] = Math.max(b,intervals[i][1]);al.add(temp);}else{al.add(intervals[i]);}}return al.toArray(new int[al.size()][]);}
}

题解复盘：

        跟题解中版本2的思路雷同。

---

738.单调递增的数字

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

初始思路：

        大概的思路就是，首先我们需要获取每一位的数字，然后进行比较，判断当前是否为单调递增的数字，如果是直接返回当前结果，如果不是，当前数字减1重复以上步骤。但是有点不太好写。

题解复盘：

1.如何变：

98，一旦出现strNum[i - 1] > strNum[i]的情况（非单调递增），首先想让strNum[i - 1]--，然后strNum[i]给为9，这样这个整数就是89，即小于98的最大的单调递增整数。

2.从前向后还是从后向前：

从前向后遍历的话，遇到strNum[i - 1] > strNum[i]的情况，让strNum[i - 1]减一，但此时如果strNum[i - 1]减一了，可能又小于strNum[i - 2]。

这么说有点抽象，举个例子，数字：332，从前向后遍历的话，那么就把变成了329，此时2又小于了第一位的3了，真正的结果应该是299。

那么从后向前遍历，就可以重复利用上次比较得出的结果了，从后向前遍历332的数值变化为：332 -> 329 -> 299

class Solution {public int monotoneIncreasingDigits(int n) {String s = String.valueOf(n);char[] chars = s.toCharArray();int start = s.length();for (int i = s.length() - 2; i >= 0; i--) {if (chars[i] > chars[i + 1]) {chars[i]--;start = i+1;}}for (int i = start; i < s.length(); i++) {chars[i] = '9';}return Integer.parseInt(String.valueOf(chars));}
}