文章解读与仿真程序复现思路——电力系统自动化EI\CSCD\北大核心《计及调频能力和经济效益的储能集群多状态区间优化策略》-编程知识

这个标题提到了三个关键概念：储能集群、调频能力和经济效益，以及多状态区间优化策略。下面我将为你解释每个概念的含义，并对整个标题进行解读。

首先，"储能集群"是指将多个储能系统连接在一起形成一个集群，以便更高效地管理能量存储和释放。这些储能系统可以包括电池、超级电容器、抽水蓄能等，用于在能源系统中存储电力供应过剩或需要时释放电能。储能集群可以提供电网稳定性、调节能源波动以及提供备用能源等功能。

其次，"调频能力"是指储能集群调节能源的能力，即能够根据电网需求快速响应并调整供应的能量。调频通常用于平衡电力系统中的瞬时电力需求和供应之间的差距。储能集群的调频能力可以通过灵活地储存和释放能量来帮助实现电力系统的平衡和稳定。

"经济效益"是指储能集群的使用对经济的影响。储能集群可以提供多种经济效益，例如降低电力系统的运营成本、减少对传统发电厂的依赖和提供可再生能源的集成等。通过优化储能集群的操作策略，可以最大程度地实现经济效益。

最后，"多状态区间优化策略"是指在储能集群中应用一种优化策略，以在不同的状态和区间下实现最佳的能量管理。储能系统可以处于不同的状态，如充电、放电和待机状态，并在不同的区间内操作，如电荷/放电速率、能量储存容量等。优化策略可以考虑电力需求、成本因素和能量供应的可持续性等因素，以在多个状态和区间下找到最佳的操作方法。

因此，这个标题所述的内容是：研究一种优化策略，在考虑到储能集群的调频能力和经济效益的前提下，实现在不同的状态和区间下对储能集群进行最佳化管理。这个研究的目的是为了提高储能集群的经济性和灵活性，同时满足电力系统的调节要求。

摘要：可再生能源发电系统的快速增长使得电力系统的频率安全面临着挑战。针对分布式储能集群二次调频过程中所面临的问题，提出一种计及调频能力和经济效益的储能集群多状态区间优化策略。该策略依据荷电状态将所有储能单元划分为多个状态区间，再结合自动发电控制指令及各区间的极限功率确定优化区间。针对非优化区间内的单元，输出功率直接由出力优先级确定；针对优化区间内的单元，利用反映调频成本和整体荷电状态的目标函数及约束条件完成最优求解从而确定输出功率。仿真结果表明,所提策略能大大减小控制中心的运算量，功率分配结果能有效提升储能集群的二次调频能力，同时提升储能集群的经济效益。

这个摘要描述了一个针对可再生能源发电系统快速增长所带来的频率安全挑战的解决方案。它着重解决分布式储能集群在进行二次调频过程中所遇到的问题，并提出了一种称为"计及调频能力和经济效益的储能集群多状态区间优化策略"的方法。

这个策略基于电池等储能单元的荷电状态将其划分为多个状态区间，并结合自动发电控制指令以及各区间的极限功率来确定优化区间。对于处于非优化区间内的储能单元，其输出功率由预先设定的出力优先级决定；而对于位于优化区间内的储能单元，则利用反映调频成本和整体荷电状态的目标函数和约束条件来完成最优求解，从而确定输出功率。

通过仿真结果的分析表明，这种提出的策略可以显著减少控制中心的运算量。此外，所得到的功率分配结果能够有效提升储能集群在二次调频方面的能力，并同时提高储能集群的经济效益。

总体来说，这个摘要描述了一种基于多状态区间优化的储能集群管理策略，旨在解决可再生能源快速增长对电力系统频率安全所带来的挑战。该方法不仅能够提高储能集群的调频能力，还能在经济效益方面取得显著提升，并且在模拟中展现了很好的效果。

关键词:分布式储能集群; 自动发电控制;调频能力;经济效益;多状态区间;功率分配;目标函数;

分布式储能集群： 这指的是多个储能系统分布在不同地点，通过协同工作形成一个集群。这样的分布式配置使得储能能够更灵活地应对电力系统的需求，例如存储过剩能量或在需要时释放电能。
自动发电控制： 涉及到储能集群中发电单元的控制过程，这个控制过程是自动化的，可能基于预定的算法、策略或指令。通过自动发电控制，储能系统能够快速响应电力系统的需求，特别是在调频等方面。
调频能力： 这是指储能系统对电力系统频率变化的响应和调整能力。在电力系统中，调频是确保瞬时功率平衡的过程，储能系统的调频能力关乎到电力系统的稳定性和可靠性。
经济效益： 这关注储能系统的运行对整体经济的影响。优化储能系统的运行可以降低电力系统的运营成本，减少对传统发电方式的依赖，并提高可再生能源的整体经济效益。
多状态区间： 这是指将储能单元的荷电状态划分为多个不同的区间。这种分区的思想可能是为了更细致地管理储能系统的运行状态，以便更精确地应对电力系统的需求。
功率分配： 这是指确定储能集群中各个单元的输出功率的过程。在这个上下文中，功率分配是优化的核心，因为它直接影响到储能系统的性能和对电力系统需求的响应。
目标函数： 这是一个数学表达式，用于衡量优化问题中的目标。在这里，目标函数可能用来表示调频成本和整体荷电状态，是多状态区间优化过程中的优化目标。

总体来说，这些关键词揭示了一种储能集群管理策略，通过自动发电控制、调频能力优化、经济效益考虑和多状态区间划分，以目标函数为指导，实现对功率分配的优化，从而提高储能集群在电力系统中的性能和经济效益。

仿真算例：为验证本文所提多状态区间优化策略的优越性，在 MATLAB 中设计包含新能源及储能集群的区域电网。假设新能源的装机容量为 425 MW，储能的装机容量占新能源的 20%，包含 4 座类型不同的电站，每个电站由并联的 10 个可单独控制的单元构成。各电站基本参数见表 1，各单元 SOC 初始值见表 2，单元的充放电受限值分别为 0.9 和 0.1，仿真时长为 100 min。

仿真程序复现思路：

为复现上述仿真场景，我们可以采用MATLAB编写仿真脚本。以下是一个简化的示例脚本，其中使用了基本的数学运算和MATLAB的仿真工具箱函数。请注意，以下代码是简化的示例，实际应用中可能需要更详细和精细的模型和参数设置。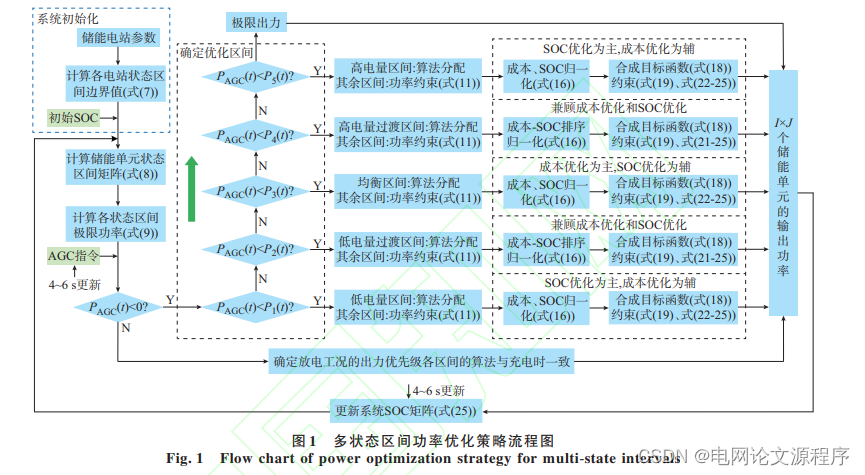

% 电站参数
Smin = 0.1;  % SOC下限
Smax = 0.9;  % SOC上限
Sp_ratio = 0.8;  % Sp相对于0.5的比例，式（6）中计算得到的% 仿真时间和时间步长
simulation_time = 100;  % 仿真时长为100 min
time_step = 1;  % 时间步长为1 min% 电站1参数
SOC_target_1 = 0.5;  % 电站1的目标SOC
initial_SOC_1 = 0.4;  % 电站1的初始SOC% 电站2参数
SOC_target_2 = Sp_ratio * 0.5;  % 电站2的目标SOC，通过式（6）计算得到
initial_SOC_2 = 0.4;  % 电站2的初始SOC% 初始化仿真结果记录
time_steps = 1:time_step:simulation_time;
SOC_1 = zeros(size(time_steps));
SOC_2 = zeros(size(time_steps));% 仿真循环
for t = 1:length(time_steps)% 电站1的调度逻辑和SOC更新charging_instruction_1 = calculate_charging_instruction(initial_SOC_1, SOC_target_1);discharging_instruction_1 = calculate_discharging_instruction(initial_SOC_1, SOC_target_1);SOC_1(t) = update_SOC(initial_SOC_1, charging_instruction_1, discharging_instruction_1, Smin, Smax, time_step);% 电站2的调度逻辑和SOC更新charging_instruction_2 = calculate_charging_instruction(initial_SOC_2, SOC_target_2);discharging_instruction_2 = calculate_discharging_instruction(initial_SOC_2, SOC_target_2);SOC_2(t) = update_SOC(initial_SOC_2, charging_instruction_2, discharging_instruction_2, Smin, Smax, time_step);% 更新初始SOC值initial_SOC_1 = SOC_1(t);initial_SOC_2 = SOC_2(t);
end% 绘制结果图
figure;
plot(time_steps, SOC_1, 'b', 'LineWidth', 2, 'DisplayName', 'Station 1');
hold on;
plot(time_steps, SOC_2, 'r', 'LineWidth', 2, 'DisplayName', 'Station 2');
xlabel('Time (min)');
ylabel('SOC');
title('SOC Simulation Results');
legend('show');% 计算充电指令
function charging_instruction = calculate_charging_instruction(current_SOC, target_SOC)charging_instruction = max(0, target_SOC - current_SOC);
end% 计算放电指令
function discharging_instruction = calculate_discharging_instruction(current_SOC, target_SOC)discharging_instruction = max(0, current_SOC - target_SOC);
end% 更新SOC的函数
function next_SOC = update_SOC(initial_SOC, charging_instruction, discharging_instruction, Smin, Smax, time_step)% 考虑充放电受限值charging_instruction = min(charging_instruction, Smax - initial_SOC);discharging_instruction = min(discharging_instruction, initial_SOC - Smin);% 简化的SOC更新算法next_SOC = initial_SOC + (charging_instruction - discharging_instruction) * time_step;% 确保SOC在合理范围内next_SOC = max(Smin, min(Smax, next_SOC));
end

请注意，以上代码仅为演示目的，实际情况可能需要更复杂的模型和算法来模拟储能电站的行为。您可能需要根据实际问题的复杂性进行更多的细化和调整。