机器调度

完整可编译运行代码见：Github::Data-Structures-Algorithms-and-Applications/_28LongestProcessingTime

问题描述

一个工厂具有 m台一模一样的机器。我们有n 个任务需要处理。设作业i的处理时间为$t_i$，这个时间包括把作业放入机器和从机器上取下的时间。所谓调度（schedule）是指按作业在机器上的运行时间分配作业，使得：

• 一台机器在同一时间内只能处理一个作业。
• 一个作业不能同时在两台机器上处理。
• 一个作业i的处理时间是t，个时间单位。

假如每台机器在0时刻都是可用的，完成时间（finish time）或调度长度（length of a schedule）是指完成所有作业的时间。在一个非抢先调度中，一项作业i在一台机器上处理，从时刻$s_i$开始，到时刻$s_i+t_i$，结束。

我们的任务是写一个程序，实现在 m 台机器上执行 n 个作业的最小完成时间的调度。但是设计一个具有多项式时间复杂性的算法(即复杂度为$n^k{m}^l$的算法，k和l是常数)来解决该问题非常难。调度问题是一个NP-复杂问题。

NP复杂问题和NP-完全问题

NP-复杂及NP-完全问题是指尚未找到具有多项式时间复杂性算法的问题。

NP-完全问题是一类判定问题，也就是说，对这类问题的每一个实例，答案为是或否。

NP-复杂问题可以是判定问题，也可以不是判定问题。

机器调度问题不是一个判定问题，因为对每一个问题实例，都是按照某种方案把作业分配给机器，以使完成时间最少。但是可以转换为判定问题。

对于机器调度问题，除了给定任务和机器外，还给定了时间TMin，要求确定是否存在一种调度，它的完成时间为 TMin 或更少。对于这类问题，答案为是或否。

NP-复杂问题的优化问题经常用**近似算法（approximation aigorithm）**解决，保证能找到近似最优解。

求解思路-最长处理时间(LPT)

在我们的调度问题中，采用了一个简单调度策略，称为最长处理时间（longest processing time，LPT），它的调度长度是最优调度长度的4/3-1/（3m）。在LPT算法中，作业按处理时间的递减顺序排列。当一个作业需要分配时，总是分配给最先变为空闲的机器。

**定理 12-2[Graham]*令 F（I）为在 m 台机器上执行作业集合 I 的最佳调度完成 时间，F（I）为采用 LPT 调度策略所得到的调度完成时间，则
$$\frac{F(I)}{F^{\ast }(I)}\le \frac{4}{3}-\frac{1}{3m}$$
可用堆来建立 LPT 调度方案，时间性能为 O（nlogn）。当n<m 时，只需要将作业 i 在0~t，时间内分配给机器i来处理。当 n>m 时，可以使用大根堆将作业按处理时间递增顺序排列。为了建立LPT调度方案，作业按相反次序进行分配。为了决定将一个作业分配给哪一台机器，必须知道哪台机器最先空闲。为此，维持一个m台机器的小根堆，元素类型为machineNode，它有数据成员avail（表示何时空闲）和id（机器编号）。machineNode类型实现()的重载。初始状态下所有machine的avail都为0。

用类jobNode表示作业，它有数据成员id（作业的唯一标识符）和time（作业需要的处理时间）。

举例

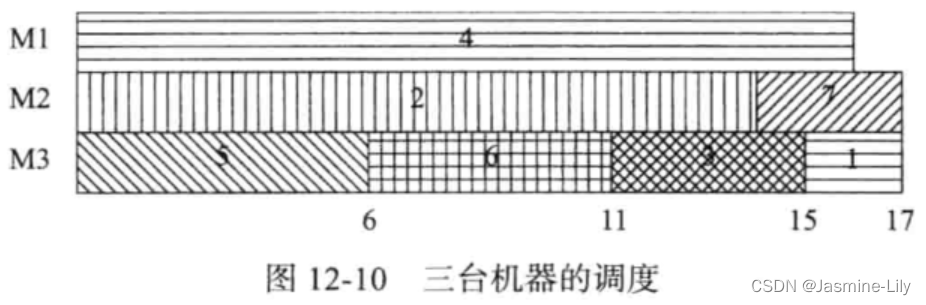
有3台机器，需要处理7个作业。7个作业的处理时间分别为（2，14，4，16，6，5，3）。3台机器的编号分别为M1、M2和M3。使用最长处理时间机器调度方法可以得到如下方案：

代码

main.cpp

#include <iostream>
#include <queue>
#include <vector>// 表示机器，id表示机器的id，avail表示机器什么时候有空
struct machineNode {int avail;int id;machineNode() {avail = 0;id = 0;}machineNode(int pid, int pavail) {avail = pavail;id = pid;}explicit operator int() const { return avail; }bool operator>(const machineNode &a) const { return avail > a.avail; }
};// 表示任务，id表示任务的id，time表示作业需要的处理时间
struct jobNode {int id;int time;jobNode() {id = 0;time = 0;}jobNode(int pid, int ptime) {id = pid;time = ptime;};explicit operator int() const { return time; }bool operator<(const jobNode &a) const { return time < a.time; }
};int main() {// 整个算法的时间复杂度为O(logn)// 初始化任务大根堆,初始化时间为O(taskVec.size()==n)const std::vector<jobNode> taskVec = {jobNode(1, 2), jobNode(2, 14), jobNode(3, 4), jobNode(4, 16), jobNode(5, 6),jobNode(6, 5), jobNode(7, 3)};std::priority_queue<jobNode, std::vector<jobNode>> tasks(taskVec.begin(), taskVec.end());// 初始化机器小根堆，初始化时间为O(machineVec.size()==m)const std::vector<machineNode> machineVec = {machineNode{1, 0}, machineNode{2, 0}, machineNode{3, 0}};std::priority_queue<machineNode, std::vector<machineNode>, std::greater<>> machines(machineVec.begin(),machineVec.end());// 执行了2n次top、2n次 pop和2n次 push操作，每次top的时间是0(1)，machines的pop和push的时间是O(logm)，tasks的pop和push的时间是O(logn)。// 因此此for循环的时间复杂度为O(nlogn)for (int i = 0; i < taskVec.size(); i++) {machineNode temp = machines.top();machines.pop();jobNode taskNode = tasks.top();tasks.pop();std::cout << "Schedule job " << taskNode.id << " on machine " << temp.id << " from " << temp.avail << " to "<< (temp.avail + taskNode.time) << std::endl;temp.avail += taskNode.time;machines.push(temp);}std::cout << std::endl;return 0;
}

运行结果

"C:\Users\15495\Documents\Jasmine\prj\_Algorithm\Data Structures, Algorithms and Applications in C++\_28LongestProcessingTime\cmake-build-debug\_28LongestProcessingTime.exe"
Schedule job 4 on machine 3 from 0 to 16
Schedule job 2 on machine 2 from 0 to 14
Schedule job 5 on machine 1 from 0 to 6
Schedule job 6 on machine 1 from 6 to 11
Schedule job 3 on machine 1 from 11 to 15
Schedule job 7 on machine 2 from 14 to 17
Schedule job 1 on machine 1 from 15 to 17Process finished with exit code 0