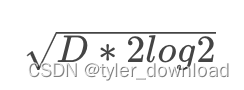目录
一、参数访问
1、目标参数
2、一次性访问所有参数
3、从嵌套块收集参数
二、参数初始化
1、内置初始化
2、自定义初始化
3、参数绑定
在选择了架构并设置了超参数后,我们就进入了训练阶段。此时,我们的目标是找到使损失函数最小化的模型参数值。经过训练后,我们将需要使用这些参数来做出未来的预测。此外,有时我们希望提取参数,以便在其他环境中复用它们,将模型保存下来,以便它可以在其他软件中执行,或者为了获得科学的理解而进行检查。
我们首先看一下具有单隐藏层的多层感知机。
import torch
from torch import nnnet = nn.Sequential(nn.Linear(4, 8), nn.ReLU(), nn.Linear(8, 1))
X = torch.rand(size=(2, 4))
net(X)tensor([[0.0374],[0.0073]], grad_fn=<AddmmBackward0>)一、参数访问
我们从已有模型中访问参数。当通过`Sequential`类定义模型时,我们可以通过索引来访问模型的任意层。这就像模型是一个列表一样,每层的参数都在其属性中。如下所示,我们可以检查第二个全连接层的参数。
print(net[2].state_dict()) # nn.Linear(4, 8):net[0] nn.ReLU():net[1] nn.Linear(8, 1):net[2]OrderedDict([('weight', tensor([[-0.1818, 0.1352, 0.2452, 0.0901, -0.0235, 0.1942, -0.3280, -0.0230]])), ('bias', tensor([0.0322]))])输出的结果告诉我们一些重要的事情:首先,这个全连接层包含两个参数,分别是该层的权重(weight)和偏置(bias)。两者都存储为单精度浮点数(float32)。注意,参数名称允许唯一标识每个参数,即使在包含数百个层的网络中也是如此。
1、目标参数
注意,每个参数都表示为参数类的一个实例。要对参数执行任何操作,首先我们需要访问底层的数值。有几种方法可以做到这一点。有些比较简单,而另一些则比较通用。下面的代码从第二个全连接层(即第三个神经网络层)提取偏置,提取后返回的是一个参数类实例,并进一步访问该参数的值。
print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)<class 'torch.nn.parameter.Parameter'>
Parameter containing:
tensor([0.0322], requires_grad=True)
tensor([0.0322])参数是复合的对象,包含值、梯度和额外信息。这就是我们需要显式参数值的原因。除了值之外,我们还可以访问每个参数的梯度。在上面这个网络中,由于我们还没有调用反向传播,所以参数的梯度处于初始状态。
print(net[2].bias.grad == None)
print(net[2].weight.grad == None)True
True2、一次性访问所有参数
当我们需要对所有参数执行操作时,逐个访问它们可能会很麻烦。当我们处理更复杂的块(例如,嵌套块)时,情况可能会变得特别复杂,因为我们需要递归整个树来提取每个子块的参数。下面,我们将通过演示来比较访问第一个全连接层的参数和访问所有层。
print(*[(name, param.shape) for name, param in net[0].named_parameters()]) # net[0].named_parameters()方法返回一个迭代器,用于迭代每个层的参数。每个参数都是一个元组,包含参数的名称和参数本身。
print(*[(name, param.shape) for name, param in net.named_parameters()]) # net.named_parameters()方法返回一个迭代器,用于迭代整个神经网络模型net中的所有层的参数。('weight', torch.Size([8, 4])) ('bias', torch.Size([8]))
('0.weight', torch.Size([8, 4])) ('0.bias', torch.Size([8])) ('2.weight', torch.Size([1, 8])) ('2.bias', torch.Size([1]))在这个上下文中,星号*被用作参数解包操作符。它的作用是将列表或元组中的元素解包成单独的参数,然后传递给函数。
使用解包操作符*可以将列表或元组中的元素作为单独的参数传递给函数,而不是将整个列表或元组作为一个参数传递。这在需要将可变数量的参数传递给函数时非常有用,可以方便地传递多个参数而无需显式地指定参数的个数。在这个例子中,print函数会将解包后的参数逐个打印出来。
这为我们提供了另一种访问网络参数的方式,如下所示。
net.state_dict()['2.bias'].datatensor([0.0887])3、从嵌套块收集参数
让我们看看,如果我们将多个块相互嵌套,参数命名约定是如何工作的。我们首先定义一个生成块的函数(可以说是“块工厂”),然后将这些块组合到更大的块中。
def block1():return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),nn.Linear(8, 4), nn.ReLU())def block2():net = nn.Sequential()for i in range(4):# 在这里嵌套net.add_module(f'block {i}', block1()) # .add_module()可以传一个字符串进去给block命名return netrgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)tensor([[0.2596],[0.2596]], grad_fn=<AddmmBackward0>)设计了网络后,我们看看它是如何工作的。
print(rgnet)Sequential((0): Sequential((block 0): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 1): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 2): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU())(block 3): Sequential((0): Linear(in_features=4, out_features=8, bias=True)(1): ReLU()(2): Linear(in_features=8, out_features=4, bias=True)(3): ReLU()))(1): Linear(in_features=4, out_features=1, bias=True)
)因为层是分层嵌套的,所以我们也可以像通过嵌套列表索引一样访问它们。下面,我们访问第一个主要的块中、第二个子块的第一层的偏置项。
rgnet[0][1][0].bias.datatensor([ 0.1999, -0.4073, -0.1200, -0.2033, -0.1573, 0.3546, -0.2141, -0.2483])二、参数初始化
知道了如何访问参数后,现在我们看看如何正确地初始化参数。深度学习框架提供默认随机初始化,也允许我们创建自定义初始化方法,满足我们通过其他规则实现初始化权重。
默认情况下,PyTorch会根据一个范围均匀地初始化权重和偏置矩阵,这个范围是根据输入和输出维度计算出的。PyTorch的`nn.init`模块提供了多种预置初始化方法。
1、内置初始化
让我们首先调用内置的初始化器(nn.init)。下面的代码将所有权重参数初始化为标准差为0.01的高斯随机变量,且将偏置参数设置为0。
def init_normal(m):if type(m) == nn.Linear:nn.init.normal_(m.weight, mean=0, std=0.01)nn.init.zeros_(m.bias)
net.apply(init_normal)
net[0].weight.data[0], net[0].bias.data[0](tensor([-0.0214, -0.0015, -0.0100, -0.0058]), tensor(0.))我们还可以将所有参数初始化为给定的常数,比如初始化为1。
def init_constant(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 1)nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0], net[0].bias.data[0](tensor([1., 1., 1., 1.]), tensor(0.))我们还可以对某些块应用不同的初始化方法。例如,下面我们使用Xavier初始化方法初始化第一个神经网络层,然后将第三个神经网络层初始化为常量值42。
def init_xavier(m):if type(m) == nn.Linear:nn.init.xavier_uniform_(m.weight)
def init_42(m):if type(m) == nn.Linear:nn.init.constant_(m.weight, 42)net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)tensor([ 0.5236, 0.0516, -0.3236, 0.3794])
tensor([[42., 42., 42., 42., 42., 42., 42., 42.]])2、自定义初始化
有时,深度学习框架没有提供我们需要的初始化方法。在下面的例子中,我们使用以下的分布为任意权重参数定义初始化方法:

同样,我们实现了一个`my_init`函数来应用到`net`。
def my_init(m):if type(m) == nn.Linear:print("Init", *[(name, param.shape)for name, param in m.named_parameters()][0])nn.init.uniform_(m.weight, -10, 10)m.weight.data *= m.weight.data.abs() >= 5net.apply(my_init)
net[0].weight[:2]Init weight torch.Size([8, 4])
Init weight torch.Size([1, 8])
tensor([[5.4079, 9.3334, 5.0616, 8.3095],[0.0000, 7.2788, -0.0000, -0.0000]], grad_fn=<SliceBackward0>)注意,我们始终可以直接设置参数。
net[0].weight.data[:] += 1
net[0].weight.data[0, 0] = 42
net[0].weight.data[0]tensor([42.0000, 10.3334, 6.0616, 9.3095])3、参数绑定
有时我们希望在多个层间共享参数:我们可以定义一个稠密层,然后使用它的参数来设置另一个层的参数。
# 我们需要给共享层一个名称,以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),shared, nn.ReLU(),shared, nn.ReLU(),nn.Linear(8, 1))
net(X)
# 检查参数是否相同
print(net[2].weight.data[0] == net[4].weight.data[0])
net[2].weight.data[0, 0] = 100
# 确保它们实际上是同一个对象,而不只是有相同的值
print(net[2].weight.data[0] == net[4].weight.data[0])tensor([True, True, True, True, True, True, True, True])
tensor([True, True, True, True, True, True, True, True])这个例子表明第三个和第五个神经网络层的参数是绑定的。它们不仅值相等,而且由相同的张量表示。因此,如果我们改变其中一个参数,另一个参数也会改变。
这里有一个问题:当参数绑定时,梯度会发生什么情况?答案是由于模型参数包含梯度,因此在反向传播期间第二个隐藏层(即第三个神经网络层)和第三个隐藏层(即第五个神经网络层)的梯度会加在一起。