1. 验证回文串

题目链接：验证回文串 - leetcode
题目描述：
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
题目归纳：
和传统的回文串验证不一样，有一些非(字母数字)字符，不过大致思路一样。

解题思路：
(1) 解法一： 见代码。

Python3

class Solution:def isPalindrome(self, s: str) -> bool:n = len(s)left, right = 0, n-1while left < right:while left < right and not s[left].isalnum(): # 跳过非(字母数字)字符left += 1while left < right and not s[right].isalnum():# 跳过非(字母数字)字符right -= 1if left < right:if s[left].lower() != s[right].lower(): # 有不一样则return Falsereturn Falseleft += 1right -= 1return True # 遍历结束代表是这个题目说的回文串

2. 判断子序列

题目链接：判断子序列 - leetcode
题目描述：
给定字符串 s 和 t ，判断 s 是否为 t 的子序列。字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
题目归纳：
注意，是子序列，而不是子串。子序列可以间隔跳跃，子串必须是连续的。

解题思路：
(1) 解法一： 双指针。一个一个比较，直到s或t任意一方遍历到末尾，最后若遍历s的指针到达了末尾，则说明s是t的子序列，否则不是。
(2) 解法二： 动态规划。略，时间复杂度和空间复杂度都不如双指针，请看官方题解。

Python3

双指针

时间复杂度：$O(n+m)$，其中 $n$ 为 $s$ 的长度，$m$ 为 $t$ 的长度。每次无论是匹配成功还是失败，都有至少一个指针发生右移，两指针能够位移的总距离为 $n+m$。
空间复杂度：$O(1)$。

class Solution:def isSubsequence(self, s: str, t: str) -> bool:# 双指针解法，注意：判断s是否是t的子序列# 贪心匹配，匹配位置更前的字符即可i = 0 # s指针j = 0 # t指针while i < len(s) and j < len(t): # 有j+=1，循环一定能跳出# (1)匹配成功，同时右移if s[i] == t[j]:i += 1j += 1# (2)匹配成功或失败，t指针都右移else:j += 1# (3)若i到达了s字符串末尾，则匹配完成，返回trueif i == len(s):return Trueelse:return False

3. 两数之和 II - 输入有序数组

题目链接：两数之和 II - 输入有序数组 - leetcode
题目描述：
给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。你所设计的解决方案必须只使用常量级的额外空间。
题目归纳：
(1) 数组非递减。
(2) 数组元素可能有正负，target也可能有正负。
(3) 最终返回结果是，一个数组，但只有两个元素值。
(4) 每个输入答案唯一。
(5) 常量级别的空间。看到这种条件一般多是双指针或者多指针解法。

解题思路：
(1) 解法一： 二分查找，时间复杂度不如双指针，请看官方题解。
(2) 解法二： 双指针。只要numbers[left] + numbers[right] < target，left就往右加，反之若numbers[left] + numbers[right] > target，right就往左减，为什么这样可以？因为最终答案一定在数组的边界以内，之所以会有困扰，肯定是因为在数学上理解$x+y=target$，画下这个函数的直线，从$x+y<target$的区域出发，会有两个方向可以落到$x+y=target$直线上，分别是$x$正半轴方向与$y$正半轴方向。具体的可以看官方题解。

Python3

class Solution:def twoSum(self, numbers: List[int], target: int) -> List[int]:left, right = 0, len(numbers) - 1while left < right:sum = numbers[left] + numbers[right]if (sum == target):return [left+1, right+1]elif sum < target:left += 1 # 最终left是不断相加，到达目标点，不要考虑left可能存在--情况else:right -= 1 # 最终right是不断相减，到达目标点，不要考虑right可能存在++情况return [-1,-1]

4. 盛最多水的容器

题目链接：盛最多水的容器 - leetcode
题目描述：
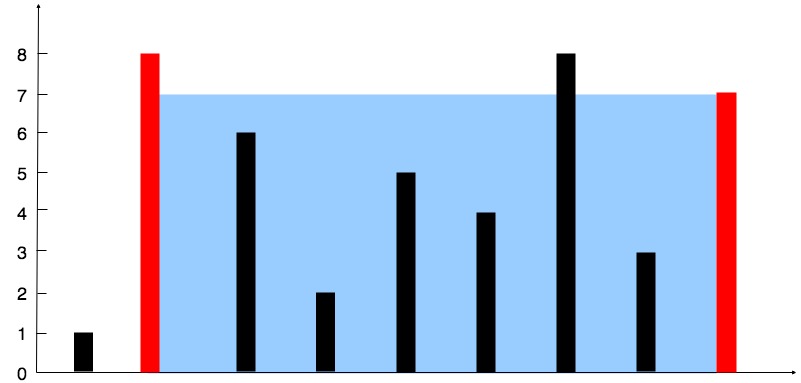
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。说明：你不能倾斜容器。

题目归纳：
(1) 水的高度最多到低的槽板。
(2) 更高的槽板不能动，要尽可能的把更低的槽板通过移动换掉。
(3) 水量公式$capacity=(r-l+1)\ast min(height[l],height[r])$，即宽度*高度。
(4) 记录历史最大水量值$ma{x}_{c}apacity$。

解题思路：
(1) 解法： 双指针。

Python3

双指针

class Solution:def maxArea(self, height: List[int]) -> int:# 双指针解法max_capacity = 0n = len(height)l, r = 0, n-1while l < r:# 求当前容量capacity = (r - l) * min(height[l], height[r])# 记录历史最大容量max_capacity = max(capacity, max_capacity)# 移动高度低的一方if(height[l] <= height[r]):l += 1else:r -= 1return max_capacity

5. 三数之和

题目链接：三数之和 - leetcode
题目描述：
给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。注意：答案中不可以包含重复的三元组。
题目归纳：
(1) $i\ne j,i\ne k,j\ne k$
(2) $nums[i]+nums[j]+nums[k]=0$
(3) 找到所有这样的$nums[i],nums[j],nums[k]$三元组，并将其作为数组返回。
(4) 输出的顺序和三元组的顺序并不重要。也就是说，$(a,b,c)$和$(a,c,b)$是同样的三元组，那不如假设返回的三元组一定满足$a\le b\le c$。因此涉及到了排序。
(题外) 假设$nums[i]=a$是已知的，那么就变成了在两个有序数组(都是nums)中寻找$nums[j]=b、nums[k]=c$满足$b+c=-a$，这里再看到上面的第3题 两数之和 II - 输入有序数组，熟悉的感觉来了，就回归到了$target=-a$，数组为排序后的$nums[i:]$，而之所以不这样做，是因为，这样会产生$(a,b,c)$和$(a,c,b)$这样的三元组，在这道题中，这样是重复的。

解题思路：
(1) 解法： 排序+双指针。来自官方解答。

class Solution:def threeSum(self, nums: List[int]) -> List[List[int]]:n = len(nums)nums.sort()ans = list()# 枚举 afor i in range(n): # 循环(1)# 需要和上一次枚举的数不相同，若相同则下一轮循环if i > 0 and nums[i] == nums[i-1]:continue# c 对应的指针初始指向数组的最右端k = n - 1target = -nums[i]# 枚举 bfor j in range(i+1, n): # 循环(2)# 需要和上一次枚举的数不相同，若相同则下一轮循环if j > i+1 and nums[j] == nums[j-1]:continue# j<k:保证 b 的指针在 c 的指针的左侧while j < k and nums[j] + nums[k] > target:k -= 1# 不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环if j == k:breakif nums[j] + nums[k] == -nums[i]:ans.append([nums[i], nums[j], nums[k]])return ans