[Unity]运行时创建线(贝塞尔的运用)
1. 实现的目标
在运行状态下创建一条可以使用贝塞尔方法实时编辑的网格曲线。
2. 原理介绍
2.1 曲线的创建
unity建立网格曲线可以参考Unity程序化网格体的实现方法。主要分为顶点,三角面,UV和法线。笔者有类似的文章unity 线绳管道纯代码创建方法_,详细的讲解了网格线的创建方法,这次的不同点在于法线的确立方法上。
2.2贝塞尔曲线点的确立
笔者有文章Unity 贝塞尔曲线的创建_描述了贝塞尔的创建方法。
3. 实现过程
3.1曲线的创建方法
线的组成原理
曲线由横截面圆和中心轴线组成。横截面的法线方向为前后两点向量差,如下图绿色线为中心轴线,A点为横截面所在点,横截面的法线方法为向量 A D ⃗ \vec{AD} AD既向量 C B ⃗ \vec{CB} CB的单位向量;终点和起点的法线方向为自身和前点或者后一点的向量。

代码源码
3.1.1 横截圆的创建
#region 横切圆创建/// <summary>/// 得到管线横切圆/// </summary>/// <param name="Count">段数</param>/// <param name="R">半径</param>/// <returns></returns>Vector3[] CircularSection(int Count, float R){Vector3[] vector3s = new Vector3[Count];float angle = 360 / Count;Vector3 vector3 = new Vector3(R, 0, 0);for (int i = 0; i < Count; i++){//根据角度得到圆的分布点vector3s[i] = vector3.ToAngle(angle * i, Vector3.zero, Vector3.forward);}return vector3s;}#endregion vector3旋转扩展方法
/// <summary>/// 角度旋转/// </summary>/// <param name="vector3"></param>/// <param name="angle">旋转角度</param>/// <param name="center">旋转中心点</param>/// <param name="direction">旋转轴</param>/// <returns></returns>public static Vector3 ToAngle(this Vector3 vector3, float angle, Vector3 center, Vector3 direction){Vector3 pos = center;Quaternion quaternion = Quaternion.AngleAxis(angle, direction);Matrix4x4 matrix = new Matrix4x4();matrix.SetTRS(pos, quaternion, Vector3.one);vector3 = matrix.MultiplyPoint3x4(vector3);return vector3;}
3.1.2 中心线的确立
class LinePoint{Vector3 location;Vector3 direction;public Vector3 Location { get => location; set => location = value; }public Vector3 Direction { get => direction; set => direction = value; }}/// <summary>/// 中心线的确立/// </summary>/// <param name="createPoint">曲线点</param>/// <returns></returns>List<LinePoint> SetLinePoint(Vector3[] createPoint){List<LinePoint> pipePoints = new List<LinePoint>();int length = createPoint.Length;for (int i = 0; i < length; i++){if (i == 0){Vector3 tangent = (createPoint[i + 1] - createPoint[i]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}else if (i == length - 1){Vector3 tangent = (createPoint[i] - createPoint[i - 1]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}else{Vector3 tangent = (createPoint[i+1] - createPoint[i - 1]).normalized;//法线AddPipePoints(createPoint[i], tangent, ref pipePoints);}}return pipePoints;}/// <summary>/// 增加中心轴线点/// </summary>/// <param name="location">位置</param>/// <param name="direction">法线</param>void AddPipePoints(Vector3 location, Vector3 direction, ref List<LinePoint> pipePoints){LinePoint pipePoint = new LinePoint();pipePoint.Location = location;pipePoint.Direction = direction;pipePoints.Add(pipePoint);}
3.1.3网格创建
/// <summary>/// 立体网格创建/// </summary>/// <param name="createPoint">创建的点数据</param>/// <param name="circularCount">圆的段数</param>/// <param name="circularR">圆的半径</param>/// <returns></returns>public Mesh CreateLine3D(Vector3[] createPoint, int circularCount, float circularR){//截面圆Vector3[] circul = CircularSection(circularCount, circularR);//中心线List<LinePoint> centreLine = SetLinePoint(createPoint);//网格点数据Vector3[] meshPoint = CreateMeshPoint(centreLine, circul);float uvX = Vector3.Distance(circul[0], circul[1]);//返回网格return CreatMesh(centreLine, meshPoint, circul.Length, uvX);}
/// <summary>/// 创建网格点数据/// </summary>/// <param name="linePoint"></param>/// <param name="circular"></param>/// <returns></returns>Vector3[] CreateMeshPoint(List<LinePoint> linePoint, Vector3[] circular){int length = linePoint.Count;int circularCount = circular.Length;Vector3[] meshPoint = new Vector3[length * circularCount];for (int i = 0; i < length; i++){for (int j = 0; j < circularCount; j++){meshPoint[(i * circularCount) + j] = circular[j].FromToMoveRotation(linePoint[i].Location, linePoint[i].Direction);}}return meshPoint;}/// <summary>/// 网格创建/// </summary>/// <param name="linePoints">线的轴心线组</param>/// <param name="meshPoint">网格点</param>/// <param name="count">段数</param>/// <param name="uvX">uv宽度</param>/// <returns></returns>Mesh CreatMesh(List<LinePoint> linePoints, Vector3[] meshPoint, int count, float uvX){Mesh mesh = new Mesh();mesh.vertices = meshPoint;mesh.triangles = GetTriangles(linePoints.Count, count);mesh.uv = GetUV(linePoints, count, uvX);mesh.RecalculateNormals();mesh.RecalculateBounds();return mesh;}/// <param name="length">线段段数</param>/// <param name="count">横截面段数(也就是圆的段数)</param>/// <returns></returns>int[] GetTriangles(int length, int count){int[] triangles = new int[(count * (length - 1)) * 6];int k = 0;if (count == 1){for (int i = 0; i < length-1; i++){int a = i * 2;triangles[k] = a;triangles[k + 1] = a + 1;triangles[k + 2] = a + 3;triangles[k + 3] = a;triangles[k + 4] = a + 3;triangles[k + 5] = a + 2;k += 6;}}else{for (int i = 0; i < length - 1; i++){for (int j = 0; j < count; j++){if (j == count - 1){// Debug.Log("k=" + k);triangles[k] = (i * count) + j;triangles[k + 1] = (i * count) + 0;triangles[k + 2] = ((i + 1) * count) + 0;triangles[k + 3] = (i * count) + j;triangles[k + 4] = ((i + 1) * count) + 0;triangles[k + 5] = ((i + 1) * count) + j;}else{triangles[k] = (i * count) + j;triangles[k + 1] = (i * count) + j + 1;triangles[k + 2] = ((i + 1) * count) + j + 1;triangles[k + 3] = (i * count) + j;triangles[k + 4] = ((i + 1) * count) + j + 1;triangles[k + 5] = ((i + 1) * count) + j;}k += 6;}}}return triangles;}/// <summary>/// 创建uv/// </summary>/// <param name="linePoints"></param>/// <param name="count"></param>/// <param name="uvX"></param>/// <returns></returns>Vector2[] GetUV(List<LinePoint> linePoints,int count, float uvX){int length = linePoints.Count;if (count == 1) { count = 2; }Vector2[] uvs = new Vector2[(count * length)];float lineDis = 0;int k = 0;for (int i = 0; i < length; i ++){if (i != 0){lineDis += Vector3.Distance(linePoints[i].Location, linePoints[i - 1].Location);}for (int j = 0; j < count; j++){Vector2 vector2;if (j % 2 != 0){vector2 = new Vector2(uvX, lineDis);}else{vector2 = new Vector2(0, lineDis);}uvs[k] = vector2;k += 1;}}return uvs;}
3.2贝塞尔曲线的建立方法
源码
/// <summary>/// 获取绘制点/// </summary>/// <param name="controlPoints"></param>/// <param name="segmentsPerCurve"></param>/// <returns></returns>public List<Vector3> GetDrawingPoints(List<Vector3> controlPoints, int segmentsPerCurve){List<Vector3> points = new List<Vector3>();// 下一段的起始点和上段终点是一个,所以是 i+=3for (int i = 0; i <= controlPoints.Count - 4; i += 3){var p0 = controlPoints[i];var p1 = controlPoints[i + 1];var p2 = controlPoints[i + 2];var p3 = controlPoints[i + 3];float dis = Vector3.Distance(p0, p3);int count = Mathf.CeilToInt(segmentsPerCurve * dis);if (count < segmentsPerCurve){count = segmentsPerCurve;}for (int j = 0; j <= count; j++){var t = j / (float)count;points.Add(CalculateBezierPoint(t, p0, p1, p2, p3));}}return points;}// 三阶公式Vector3 CalculateBezierPoint(float t, Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3){Vector3 result;Vector3 p0p1 = (1 - t) * p0 + t * p1;Vector3 p1p2 = (1 - t) * p1 + t * p2;Vector3 p2p3 = (1 - t) * p2 + t * p3;Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;result = (1 - t) * p0p1p2 + t * p1p2p3;return result;}3.3贝塞尔曲线应用
基于上述方法实现了贝塞尔创建,保存,读取,在编辑功能。
案例下载地址
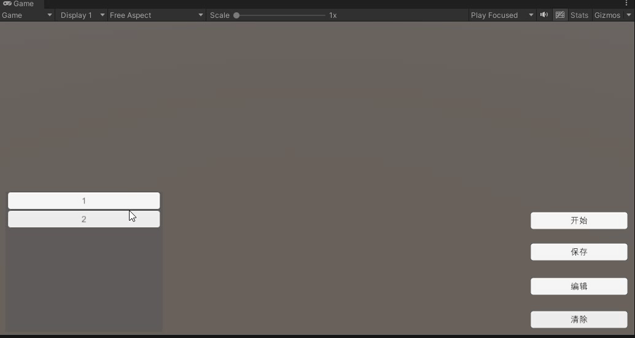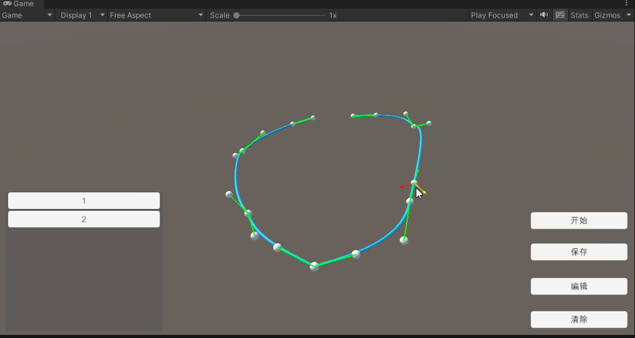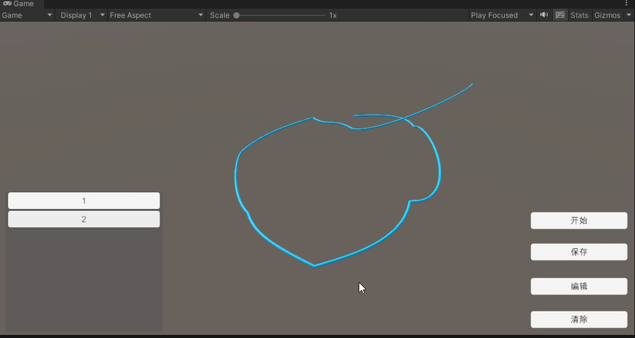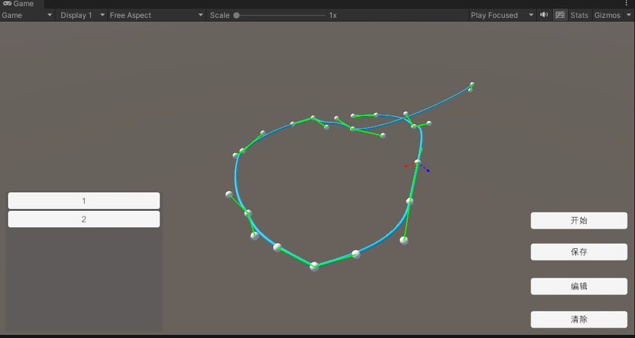
创建曲线

保存曲线
保存方法有两种分别是,长期保存和暂时保存。长期保存是将保存数据写入本地文件,项目重启也可以读取;暂时保存是在项目运行期间保存数据,重启后丢失。demo使用暂时保存的方法
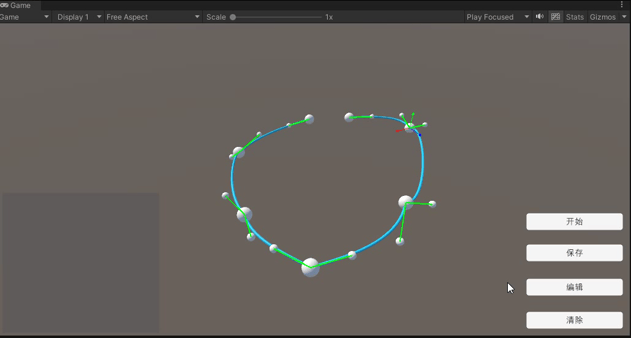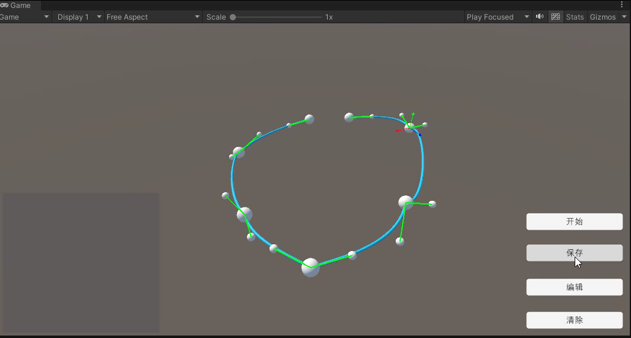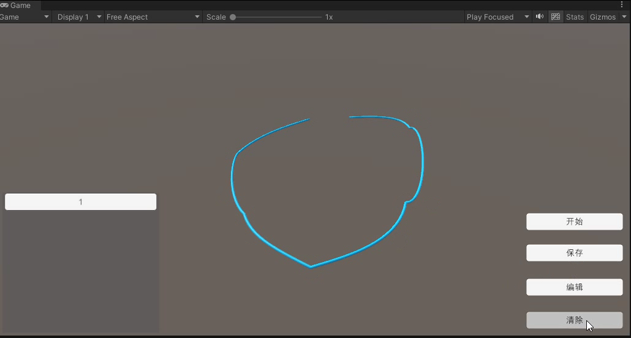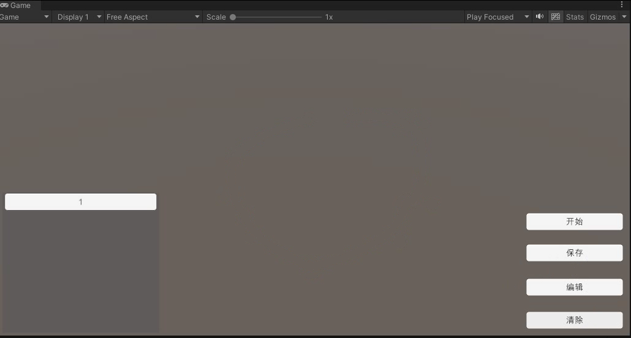
读取再编辑
读取曲线后可以继续编辑当前曲线

曲线浏览