Manacher(马拉车)算法
作用:在On的时间复杂度下,求出字符串每个回文中心的最长回文半径
回文半径:以回文中心为起点,到回文串两端的距离
如:# a # b # a #
以b为回文中心,最长回文半径就是 4(可以根据个人习惯选择是否将回文中心包括)
如果回文字符串长度为偶数,那么回文中心就无法正好落在某个字符上,所以可以在每个字符之间添加一个“#”做前置处理(包括字符串首尾)
对于求一个字符串中每个字符的最长回文半径,暴力做法是使用两层循环遍历字符串的每个字符,以遍历到的字符为中心向两边扩散:
public class Main {public static void main(String[] args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String s = br.readLine();s = getNew(s);//每个位置的最长回文半径int[]r = new int[s.length()];for (int i = 0;i < s.length();i++) {while (i-r[i] >= 0 && i+r[i] < s.length() &&s.charAt(i - r[i]) == s.charAt(i + r[i])) r[i]++;}for (int i = 0; i < s.length(); i++) {System.out.print(s.charAt(i)+" ");}System.out.println();for (int i = 0; i < s.length(); i++) {System.out.print(r[i]+" ");}}public static String getNew(String str) {String s = "#";for (int i = 0;i < str.length();i++) {s += str.charAt(i) + "#";}return s;}
}
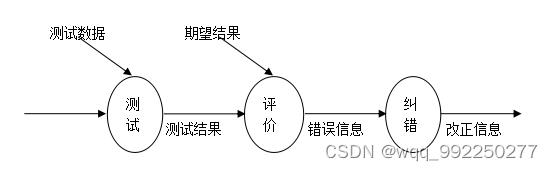
思路
利用回文串的对称性,和之前遍历过的已知的回文串,减少中心扩散的次数,这里我们要维护一个使区间右端最靠右的区间
设有字符串S,S的l到r区间是回文串,mid为回文中心,现要求以i为回文中心的最长回文半径
i在区间 [ l , r ] 内:
j为i关于mid的对称点,那么:
-
以 j 为中心的回文串在 [ l , r] 内

易知,r [ i ] = r [ j ]
-
以 j 为中心的回文串有部分在[ l , r ] 外

r [ j ] 中超出 l 的那部分肯定和 r 右边不同,所以,r [ i ] = j - l + 1 = r - i + 1
-
以 j 为中心的回文串左边界与 l 重合

这时,r [ i ] 是可以大于 r [ j ] 的,就要用中心扩散来接着求 r [ i ]
i在区间 [ l , r ] 外:
这时只能用中心扩散来求 r [ i ]
示例:洛谷:P3805 【模板】manacher
求最大回文子串长度
import java.io.*;public class Main{static final int N = 22000005;public static void main(String[]args) throws IOException {BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String s = br.readLine();char[]c = s.toCharArray();char[]sc = new char[N];int[]d = new int[N];sc[0] = '#';int cnt = 0;for(int i = 0;i < c.length;i++) {sc[++cnt] = c[i];sc[++cnt] = '#';}int r = 0,len = 0,mid = 0;for(int i = 1;i < cnt;i++) {if(i <= r) d[i] = Math.min(d[(mid << 1) - i],r - i + 1);else d[i] = 1;while(i - d[i] >= 0 && sc[i+d[i]] == sc[i - d[i]]) d[i]++;//维护最靠右区间if(i + d[i] - 1 > r) {mid = i;r = i + d[i] - 1;}//这里d[i] - 1是将子串中的‘#’去掉的长度len = Math.max(len,d[i] - 1);}System.out.println(len);}
}