大多数实际工程问题常常简化为微分方程,其求解显地至关重要。
符号微积分
极限
% matlab提供的求极限函数limit(),其调用格式为
% y = limit(fun,x,x0)
% fun为要求解的函数,x为函数自变量,x0为函数自变量的取值,x趋近于x0
clc;
clear all;
close all;
syms x a % Create symbolic variables and functions
I1 = limit((sin(x) - sin(3 * x))/sin(x),x,0)
I2 = limit((tan(x) - tan(a))/(x - a),x,a)
I3 = limit((3 * x - 5)/(x^3 * sin(1/x^2)),x,inf)
运行结果如下:
I1 =-2
I2 =tan(a)^2 + 1
I3 =3
导数
diff是求微分常用的函数,其调用格式为diff(f,x,n)f为关于x求n阶导数。
clc;
clear all;
close all;
syms x y
f = sym(exp(-2 * x)*cos(3 * x^(1/2)))
diff(f,x)
g = sym('g(x,y)') % 建立抽象函数
f = sym('f(x,y,g(x,y))') % 建立复合抽象函数
diff(f,x)
diff(f,x,2)
积分
% int(f,r,x0,x1)
% f为要积分的表达式,r为积分变量,若是定积分,x0与x1为积分上下限
clc;
clear all;
close all;
syms x y z
I1 = int(sin(x*y + z),z)
I2 = int(1/(3+2*x+x^2),x,0,1)
I3 = int(1/(3+2*x+x^2),x,-inf,inf)
运行结果为:
I1 =-cos(z + x*y)
I2 =(2^(1/2)*atan(2^(1/2)/4))/2
I3 =(pi*2^(1/2))/2
微分方程的数值解
数值解,是指给出一系列对应的自变量,采用数值方法求出的解。
matlab函数调用格式为:
[t,x] = ode23('xprime',t0,tf,x0,tol,trace)
[t,x] = ode45('xprime',t0,tf,x0,tol,trace)
或
[t,x] = ode23('xprime',[t0,tf],x0,tol,trace)
[t,x] = ode45('xprime',[t0,tf],x0,tol,trace)

function dz = dzdx1(x,z)
dz(1) = z(2);
dz(2) = z(3);
dz(3) = z(3)*x^(-1) - 3 * z(2) * x^(-2) + 2 * z(1) * x^(-3) + 9 * x^(3) * sin(x);
dz = [dz(1);dz(2);dz(3)];
end
主程序如下:
clc;
clear all;
close all;
H = [0.1,60];
z0 = [1;1;1];
[x,z] = ode15s('dzdx1',H,z0);
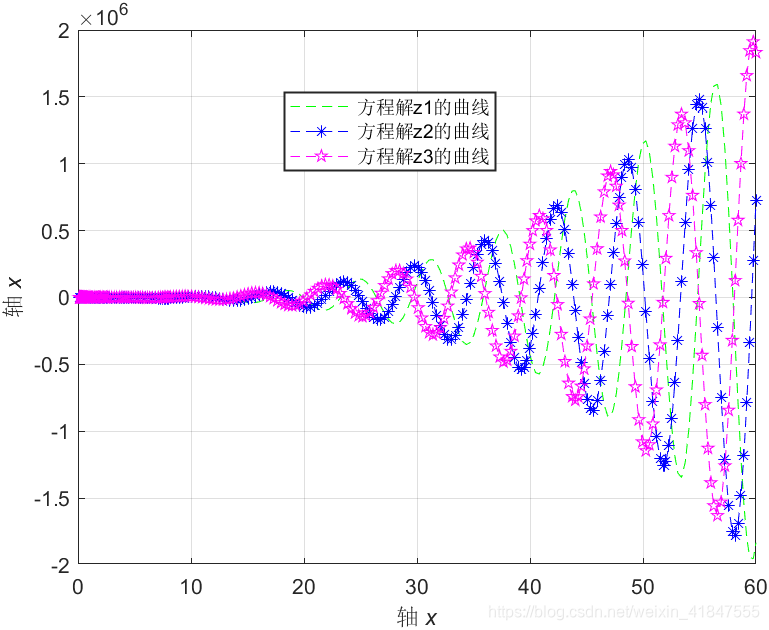
plot(x,z(:,1),'g--',x,z(:,2),'b*--',x,z(:,3),'mp--');
xlabel('轴\it x');
ylabel('轴\it x');
grid on;
legend('方程解z1的曲线','方程解z2的曲线','方程解z3的曲线')