数据结构学习笔记（七）搜索结构

文章目录

  • 1. 前言
  • 2. 概念
  • 3 静态搜索结构
    • 3.1 静态搜索表
    • 3.2 顺序搜索表
      • 3.2.1 基于有序顺序表和顺序搜索和折半搜索
  • 4 二叉搜索树
    • 4.1 搜索二叉树的类定义
    • 4.2 搜索二叉树的搜索
    • 4.3 搜索二叉树的插入
    • 4.4 搜索二叉树的删除
  • 5 AVL树
    • 5.1 平衡化旋转
      • 5.1.1 右旋：LL型状态
      • 5.1.2 左旋：RR型状态
      • 5.1.3 右旋(LL)的例子
      • 5.1.4 先左旋再右旋(LR)的操作
      • 5.1.5 先右旋再左旋(RL)的操作
      • 5.1.6 RL操作的例子
      • 5.1.7 代码实现
    • 5.2 AVL树的插入
    • 5.3 AVL树的删除
  • 6 伸展树
    • 6.1 插入
    • 6.2 查找
      • 6.3 删除
  • 7 红黑树
    • 7.1 红黑树搜索
    • 7.2 插入和删除

1. 前言

本系列笔记基于 清华大学出版社的《数据结构：用面向对象方法与C++语言描述》第二版进行学习。

2. 概念

使用基于关键码的搜索，搜索结果应该是唯一的。使用基于属性的搜索方法，搜索结果可能不唯一。
搜索的环境有两种，静态环境和动态环境。区别在于插入和删除后搜索结构会不会变化。
衡量搜索的时间效率的标准是：
在搜索过程中关键码的平均比较次数或平均读写磁盘次数，成为平均搜索长度ASL。

3 静态搜索结构

3.1 静态搜索表

最简单的基于数组的数据表类。

#include <iostream>
#include<assert.h>
using namespace std;
const int defaultSize = 100;
class dataList;class dataNode {friend class dataList;
public:dataNode(const int x = 99):key(x),data(0){}int getKey() const { return key; }void setKey(int k) { key = k; }
private:int key;                  // 关键码int data;
};class dataList {
public:dataList(int sz = defaultSize) :ArraySize(sz), CurrentSize(0) {Element = new dataNode[sz];assert(Element != NULL);}dataList(dataList& R);virtual ~dataList() { delete[]Element; }                    virtual int Length() { return CurrentSize; }               virtual int getKey(int i)const {// 提取第i个元素值（从1开始）assert(i > 0 || i <= CurrentSize);return Element[i - 1].key;}         virtual void setKey(int x, int i) {         // 修改第i个元素的值assert(i > 0 || i <= CurrentSize);Element[i - 1].key = x;}virtual int SeqSearch(const int x) const;       // 搜索virtual bool Insert(int& e1);                       // 插入virtual bool Remove(const int x, int& e1);      // 删除friend ostream& operator<<(ostream& out, const dataList& OutList);friend ostream& operator>>(istream in, dataList& InList);
protected:dataNode* Element;int ArraySize;int CurrentSize;
};class searchList :public dataList {
public:searchList(int sz = defaultSize) :dataList(sz){}virtual int SeqSearch(const int x)const;
};int main()
{std::cout << "Hello World!\n";
}bool dataList::Insert(int& e1)
{if (CurrentSize == ArraySize) return false;   // 表满，无法插入Element[CurrentSize] = e1;CurrentSize++;return true;
}bool dataList::Remove(const int x, int& e1)
{if (CurrentSize == 0)return false;int i;for (i = 0; i < CurrentSize && Element[i].key != x; i++);if (i == CurrentSize) return false;e1 = Element[i].data;Element[i] = Element[CurrentSize - 1];CurrentSize--; return true;
}ostream& operator<<(ostream& out, const dataList& OutList)
{cout << "Array Contents:\n";for (int i = 1; i < OutList.CurrentSize; i++) {cout << OutList.CurrentSize; i++;}cout << endl;cout << "Array Current Size:" << OutList.CurrentSize << endl;return out;
}ostream& operator>>(istream in, dataList& InList)
{cout << "Enter array Current Size:" << endl;in >> InList.CurrentSize;cout << "Enter array Elements:\n";for (int i = 1; i <= InList.CurrentSize; i++) {cout << "Element" << i << ":";in >> InList.Element[i - 1];}return in;
}

编译不过，因为Elements中没有设置接触到数据的函数，可以自行添加

3.2 顺序搜索表

int searchList::SeqSearch1(const int x, int loc) const
{if (loc > CurrentSize) return 0;else if (Element[loc - 1].key == x) return loc;else return SeqSearch1(x, loc + 1);
}

3.2.1 基于有序顺序表和顺序搜索和折半搜索

①顺序搜索

class SortedList : public searchList {
public:SortedList(int sz=100):searchList(sz){}~SortedList(){}int SequentSearch(const int x)const;            // 顺序搜索int BinarySearch(const int x)const;                // 折半搜索bool Insert(const int& e1);                            // 插入int Begin() { return (CurrentSize == 0) ? 0 : 1; }      // 定位第一个int Next(int i) { return(i >= 1 && i <= CurrentSize) ? i + 1 : 0; } // 定位下一个
};int SortedList::SequentSearch(const int x) const
{for (int i = 1; i <= CurrentSize; i++)if (Element[i - 1].key == x) return i;            // 成功，停止搜索else if (Element[i - 1].key > x)break;          // 不成功，停止搜索return 0;
}

②折半搜索
折半搜索又称二分搜索法
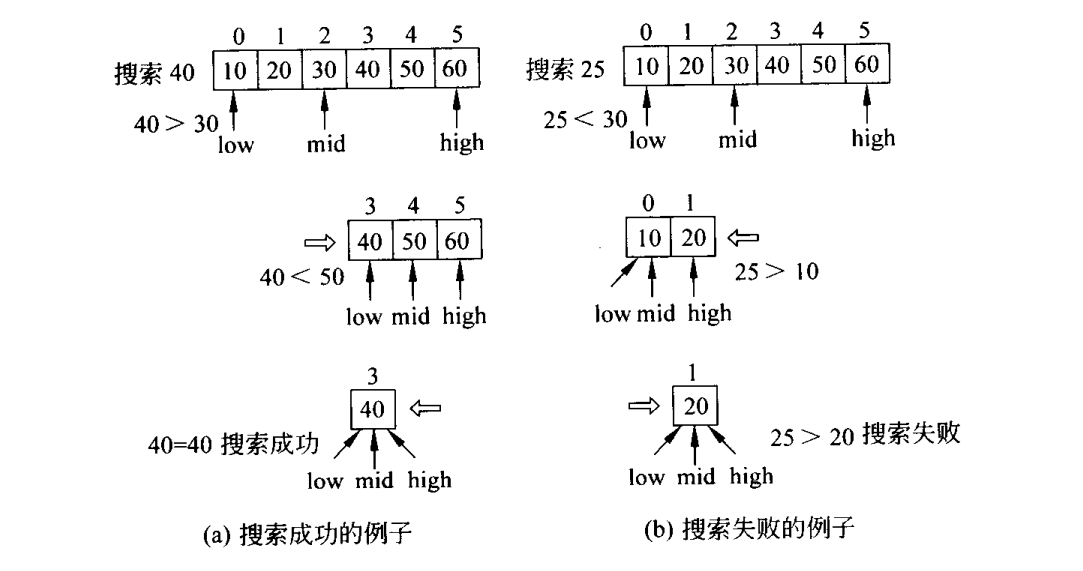
在这里插入图片描述
在这里插入图片描述
非递归算法

int SortedList::BinarySearch(const int x) const
{// 非递归算法int high = CurrentSize - 1;int low = 0;int mid;while (low <=high)          // 如果没有，最后搜索的一次是low<=high{mid = (low + high) / 2;if (x > Element[mid].key) low = mid + 1;            // 把中间的元素的后一位变成lowelse if (x < Element[mid].key) high = mid - 1;      // 把中间元素的前一位变成highelse return mid + 1;}return 0;
}

递归算法

int SortedList::BinarySearch1(const int x, int low, int high) const
{int mid = 0;if (low <= high) {mid = (low + high) / 2;if (x > Element[mid - 1].key)mid = BinarySearch1(x, mid + 1, high);          else if (x < Element[mid - 1].key)mid = BinarySearch1(x, low, mid - 1);}return mid;
}

③插入算法

void SortedList::Insert(const dataNode& e1)
{assert(CurrentSize == ArraySize);int i = 1;while (i <= CurrentSize && Element[i - 1].key <= e1.key)i++;            // 找到小于插入的结点的最大的结点for (int j = CurrentSize; j >= i; j--) Element[j] = Element[j - 1];          // 前面的赋值给另一个Element[i - 1] = e1;CurrentSize ++;
}

4 二叉搜索树

在这里插入图片描述
简单来说,就是如果找到二叉树的中序遍历,他的中序遍历一定是从小到大排序的
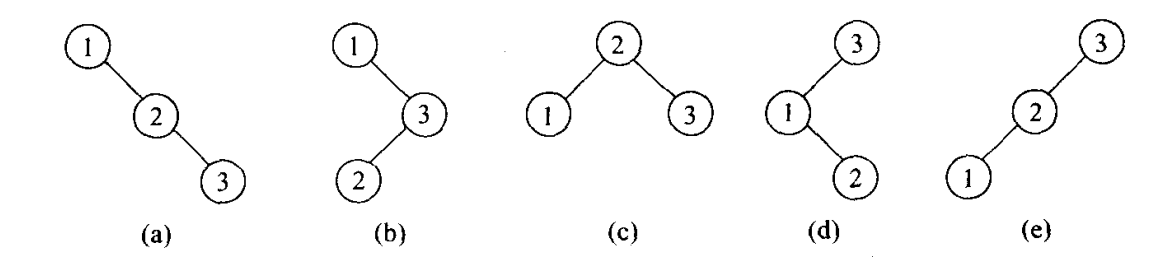
在这里插入图片描述
如上图,其中序遍历均位123

4.1 搜索二叉树的类定义

struct BSTNode
{int data;               // 二叉树节点类BSTNode* left, * right; // 左右子女BSTNode():left(NULL),right(NULL){}BSTNode(const int d, BSTNode* L = NULL, BSTNode*R =NULL):data(d),left(L),right(R){}~BSTNode(){}void SetData(int d) { data = d; }int getData() { return data; }
};class BST {
public:BST() :root(NULL) {}                                                BST(int Value);                               ~BST() {};bool Search(const int x) {return (search(x, root) != NULL) ? true : false;}BST& oprator = (const BST & R);         // 赋值void makeEmpty() { makeEmpty(root); root = NULL; }void PrintTree()const { PrintTree(root); }int Min() { return Min(root)->data; }int Max() { return Max(root)->data; }bool Insert(const int& e1) { return Insert(e1, root); }bool Remove(const int x) { return Remove(x, root); }private:BSTNode* root;int RefValue;               // 停止标志BSTNode* search(const int x, BSTNode* ptr);         // 搜索void makeEmpty(BSTNode*& ptr);                          // 置空void PrintTree(BSTNode* ptr)const;                          // 打印BSTNode* Copy(const BSTNode* ptr);                      // 复制BSTNode* Min(BSTNode* ptr)const;                                  // 求最小BSTNode* Max(BSTNode* ptr)const;                                 // 求最大bool Insert(const int& e1, BSTNode*& ptr);                      // 递归插入bool Remove(const int x, BSTNode*& ptr);                        // 删除
};

4.2 搜索二叉树的搜索

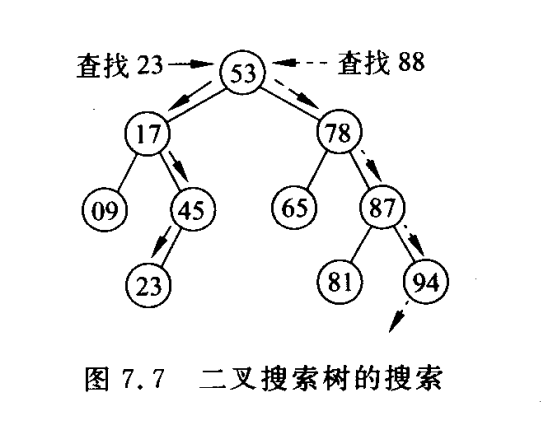
在这里插入图片描述
超级好理解

BSTNode* BST::search(const int x, BSTNode* ptr)
{if (ptr == NULL) return NULL;else if (x < ptr->data) return search(x, ptr->left);else if (x > ptr->data) return search(x, ptr->right);else return ptr;
}

4.3 搜索二叉树的插入

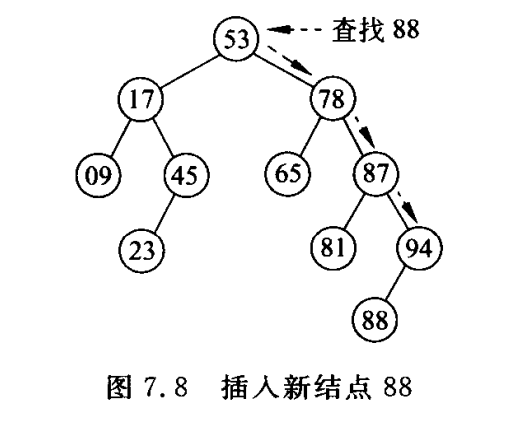
在这里插入图片描述

bool BST::Insert(const int& e1, BSTNode*& ptr)
{if (ptr == NULL) {ptr = new BSTNode(e1);if (ptr = NULL) { cout << "out of space" << endl; exit(1); }}else if (e1 < ptr->data) Insert(e1, ptr->left);         // 比结点小存左边else if (e1 > ptr->data)Insert(e1, ptr->right);   // 比节点小存右边else return false;              
}

4.4 搜索二叉树的删除

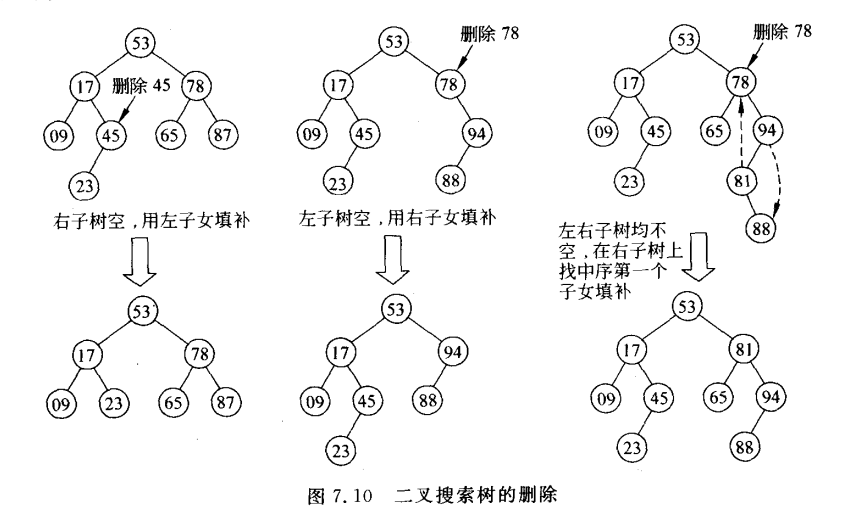
在这里插入图片描述

bool BST::Remove(const int x, BSTNode*& ptr)
{BSTNode* temp;if (ptr != NULL) {if (x < ptr->data) Remove(x, ptr->left);            // 左子树执行删除else if (x > ptr->data) Remove(x, ptr->right);    // 在右子树执行删除else if (ptr->left != NULL && ptr->right != NULL) { // 有两个子女节点temp = ptr->right;                                              // 右子树搜寻中序的第一个结点while (temp->left != NULL) temp = temp->left;ptr->data = temp->data;     // 用该节点数据代替根节点数据Remove(ptr->data, ptr->right);}else {      // 只有一个子女结点（左子结点或右子结点）           这部分是为了链接删除部分缺掉的那条线temp = ptr;if (ptr->left == NULL) ptr = ptr->right;else ptr = ptr->left;delete temp;return true;}}return false;}

5 AVL树

任一结点的右子树的高度减去左子树的高度差只能为-1，0，1

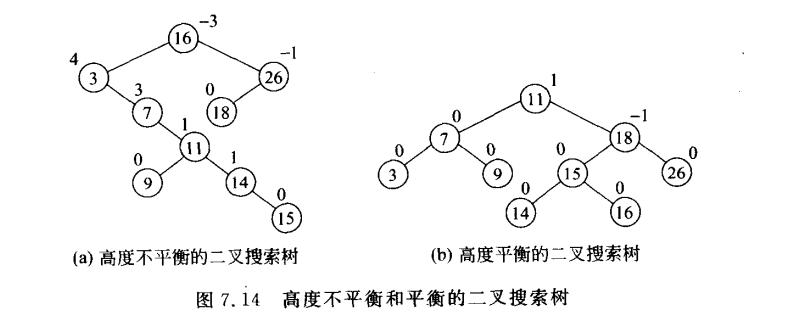
在这里插入图片描述

5.1 平衡化旋转

使不平衡的二叉搜索树变得平衡
先说插入
这里有四种情况

5.1.1 右旋：LL型状态

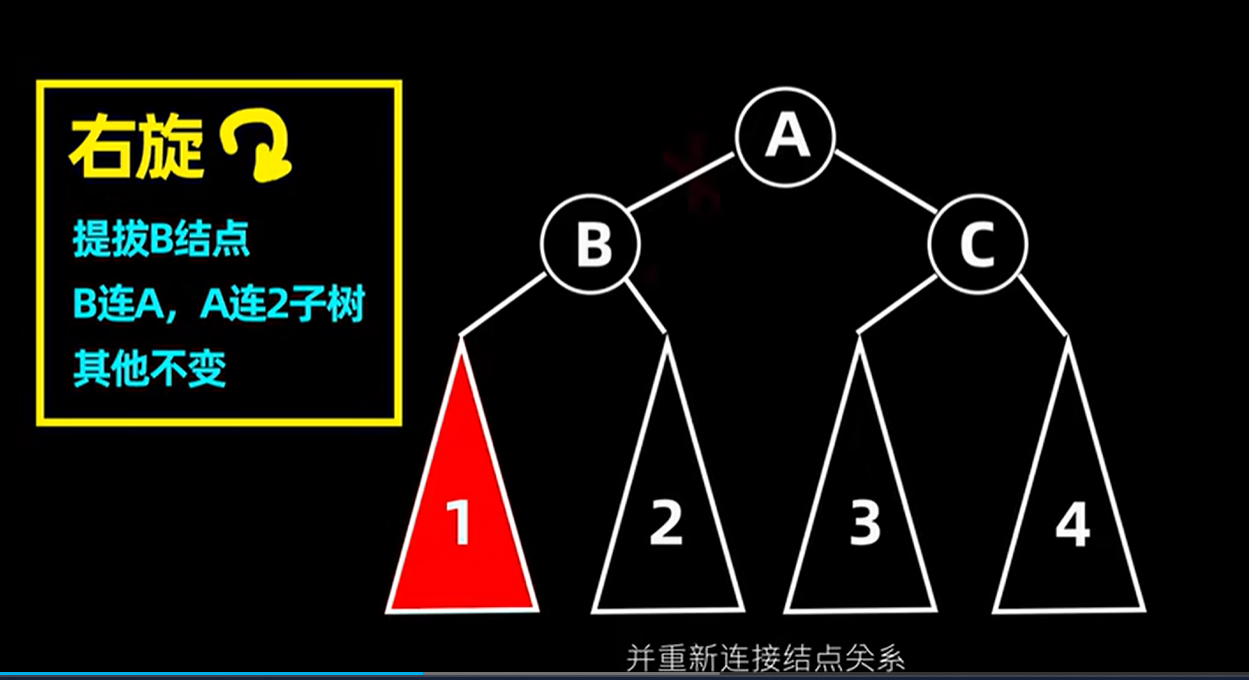
在这里插入图片描述
就是插入根节点的子结点的左子结点，
右旋相当于把树往顺时针旋转以下，把B点做成根结点，再把B结点的右子结点变成原根节点的左子节点，

旋转后变成：
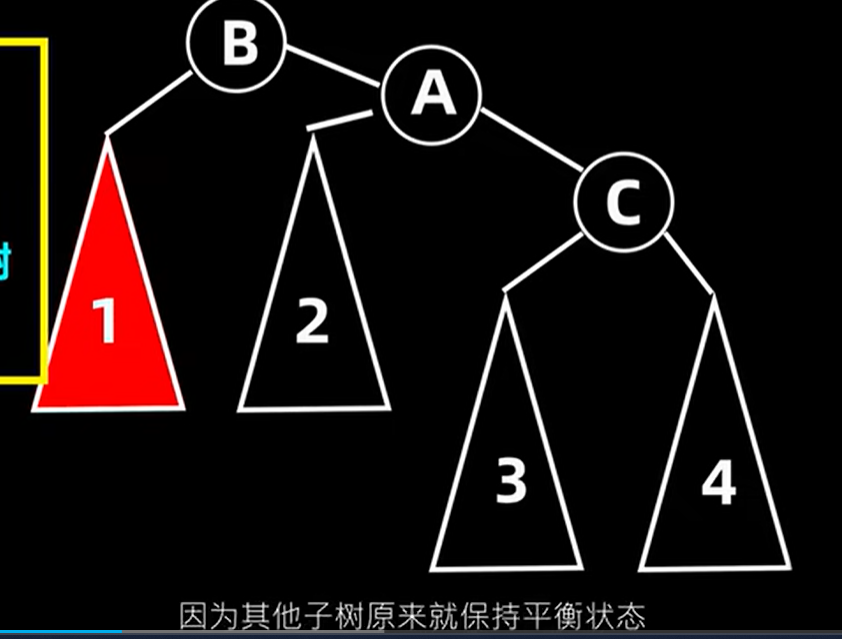
在这里插入图片描述

5.1.2 左旋：RR型状态

左旋和右旋差不多，就是插入了根节点的右子结点的右子树中。
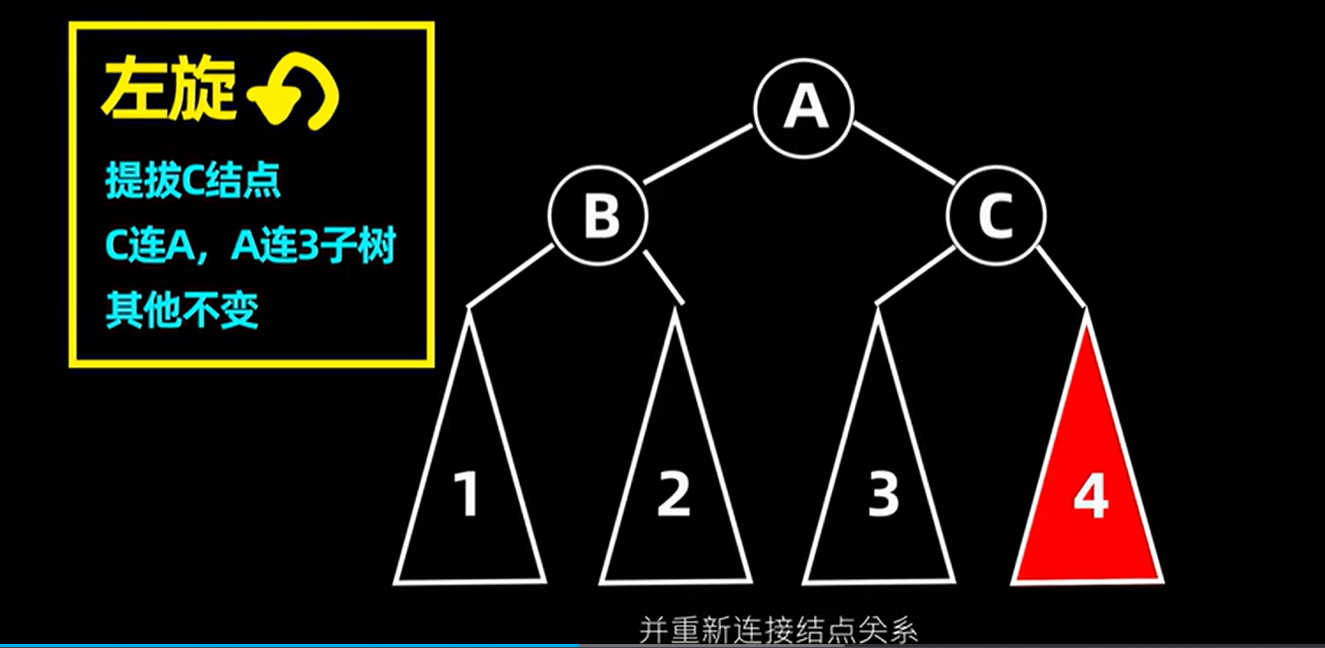
在这里插入图片描述
左旋相当于将整个树逆时针旋转了一下，将C点置为根结点，然后将A点作为C点的左子树，把原来的左子树3作为原根节点的右子树
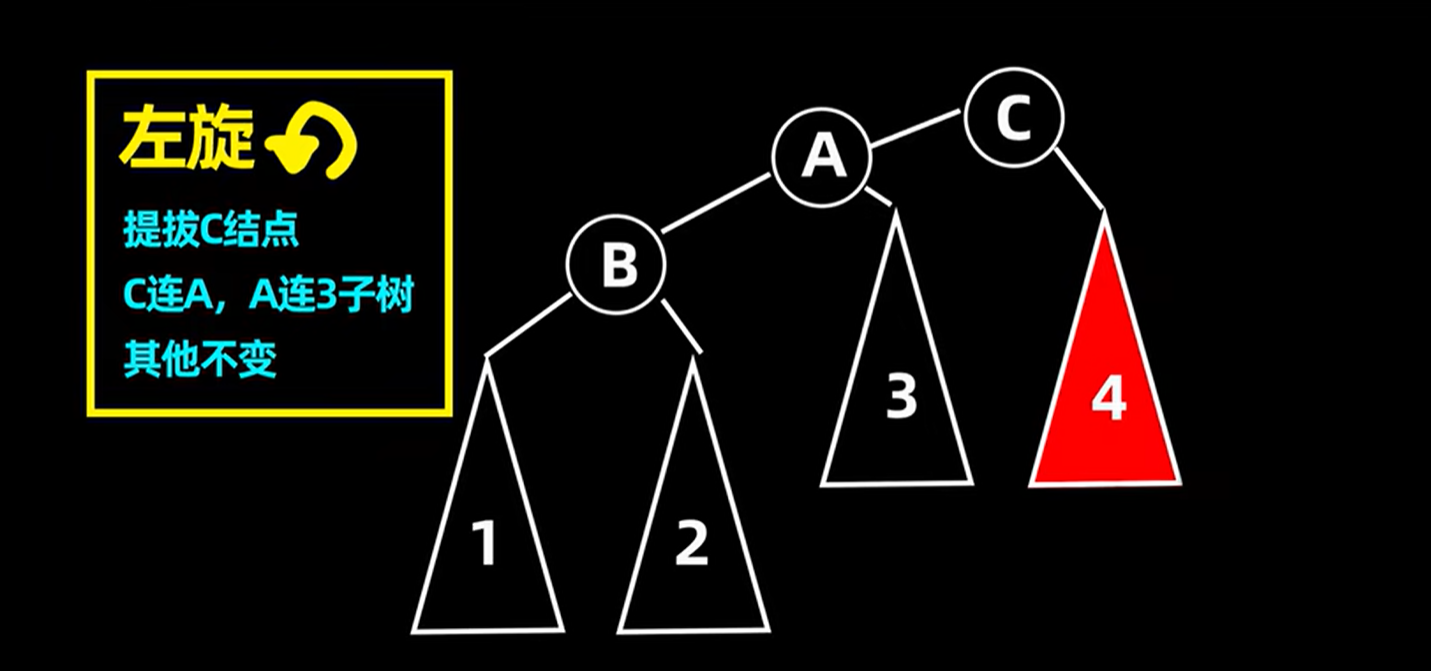
在这里插入图片描述

5.1.3 右旋(LL)的例子

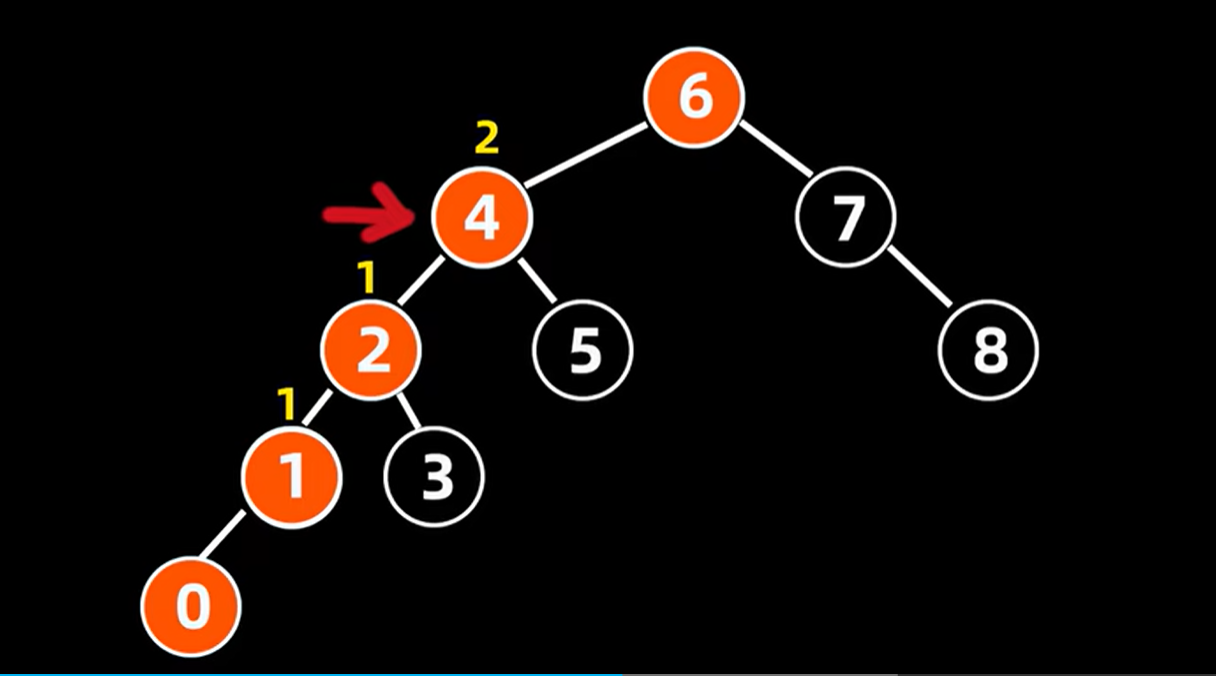
在这里插入图片描述
本次是插入0到原来的平衡树中，如图，属于LL情况，所以进行右旋操作。
找到不平衡的根结点4。所以我们要调整的树就是
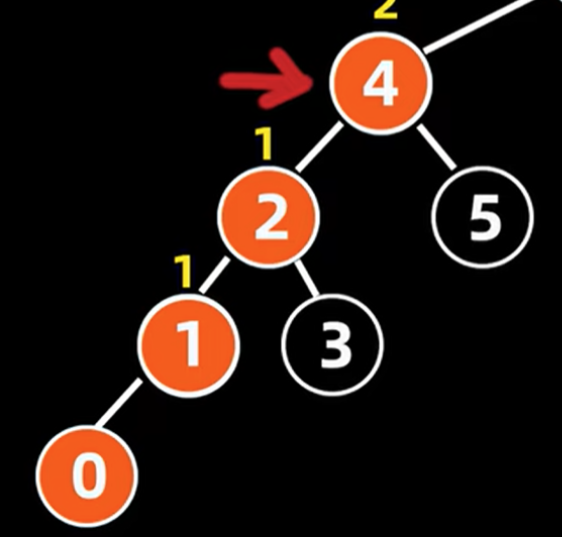
在这里插入图片描述
将原有的左子树，以2为根节点的树往上提，作为这棵树的新根节点，并把原有根节点4作为2的右子树，把2的原右子变为原根节点4的左子树
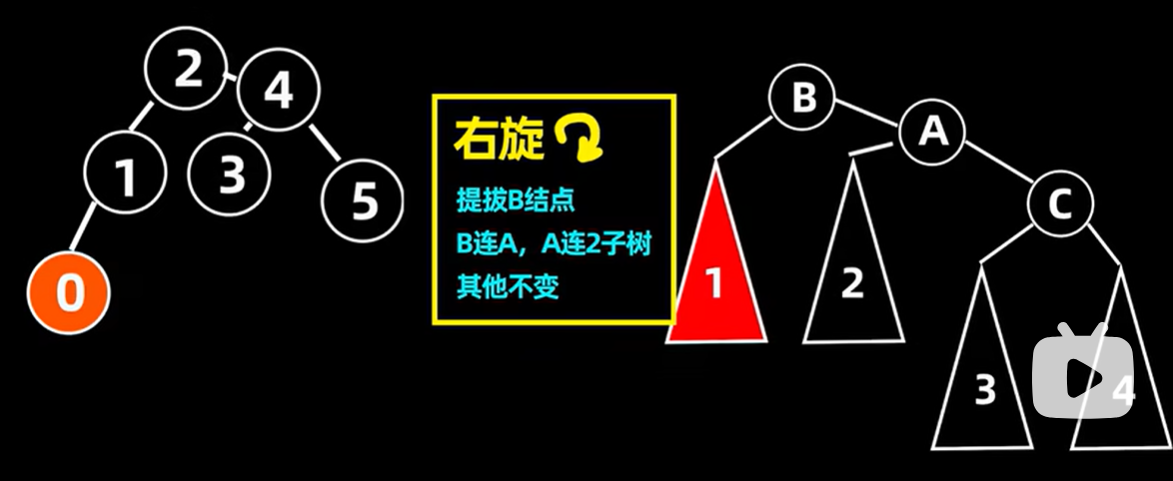
在这里插入图片描述
再把2作为原来根节点4，进行连接
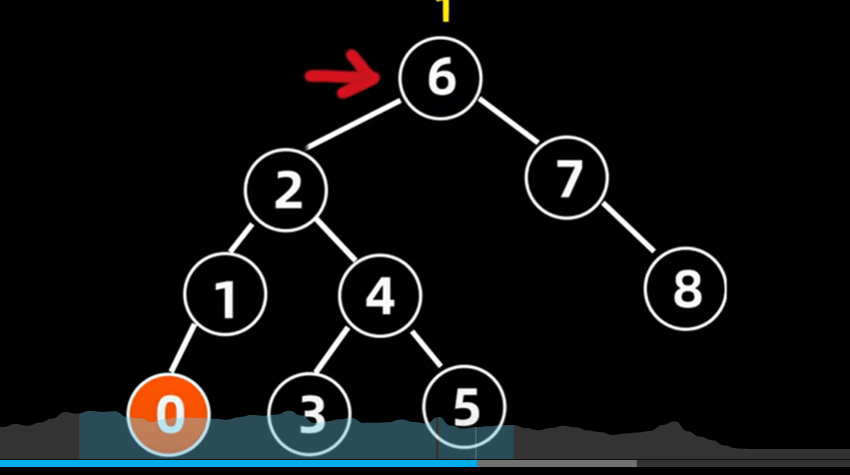
在这里插入图片描述

5.1.4 先左旋再右旋(LR)的操作

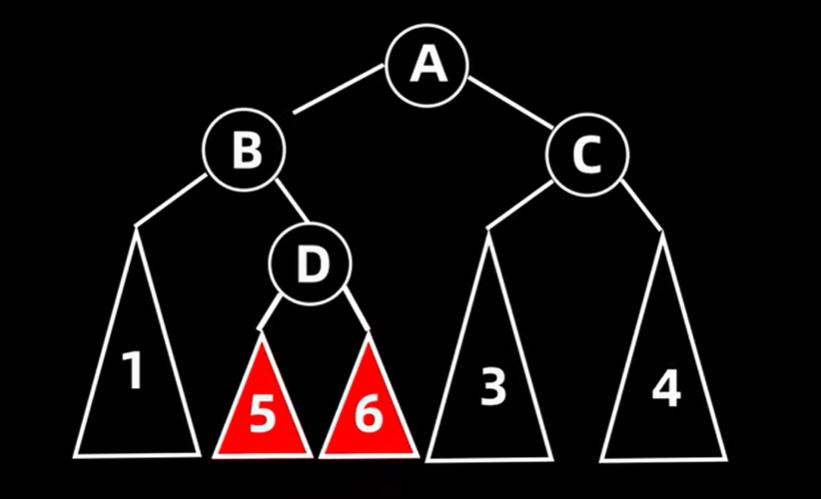
在这里插入图片描述

元素落到56都是一样的处理，把
D转换成新的根结点，把原有不平衡树的根节点A的左子女结点作为D的左子女结点，根节点A作为D的右子女结点。并把D的左子树当作B的右子树，把D的右子树当作A的左子树。
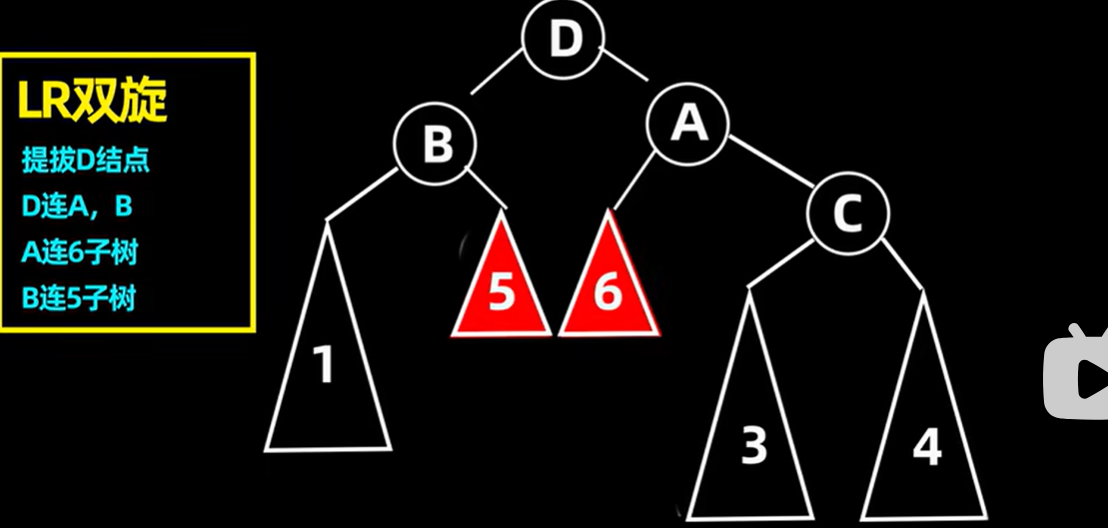
在这里插入图片描述

5.1.5 先右旋再左旋(RL)的操作

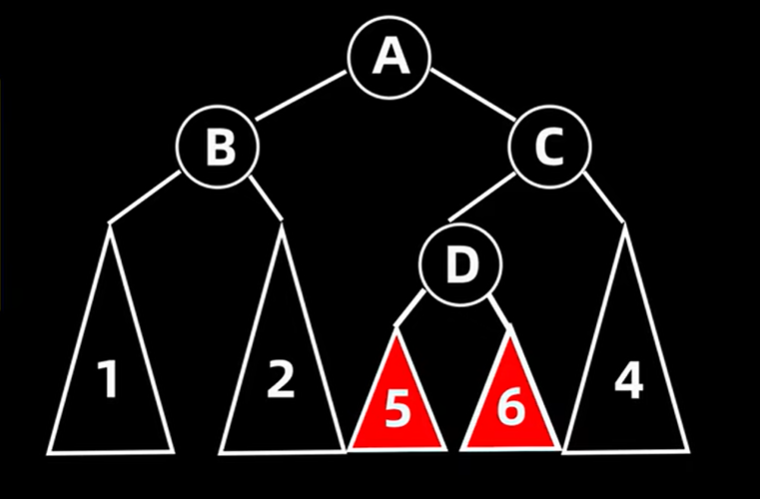
在这里插入图片描述

插入56所作的操作都一样，原理与LR差不多，把D作为新的根节点，把不平衡树的根节点A作为D的左子树，A的右子女结点C作为D的右子树。并把D的左子树转换成A的右子树，D的右子树转换为C的左子树。
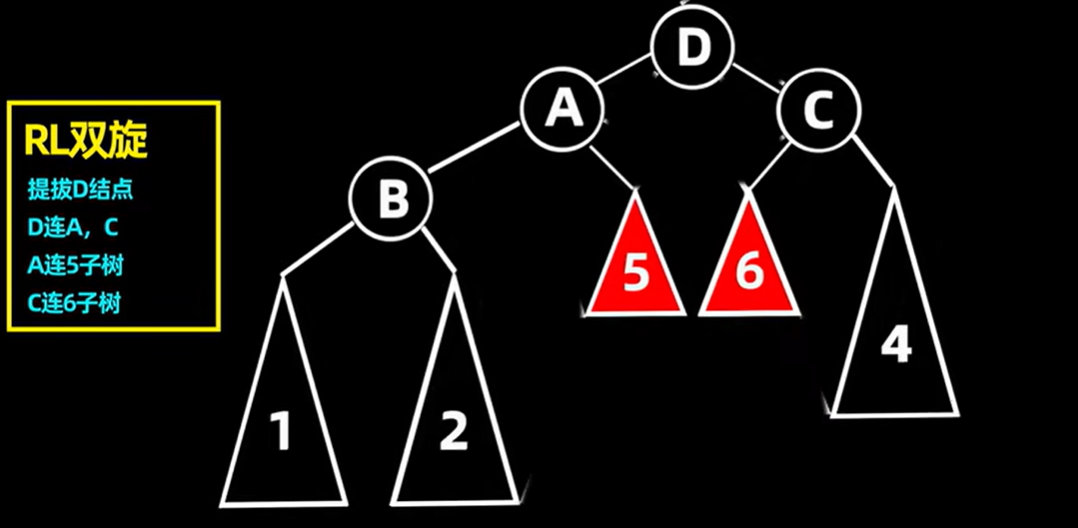
在这里插入图片描述

5.1.6 RL操作的例子

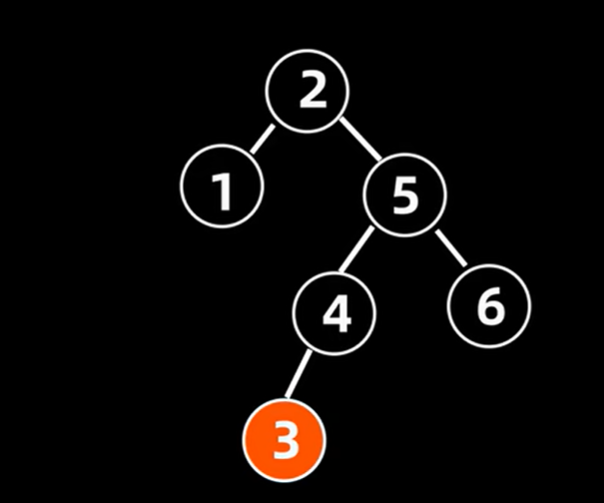
在这里插入图片描述
把4当作新父结点，将不平衡树的根节点2作为4的左子树，根节点的右结点5作为4的右子树。把4的左子树赋给2作为其右子女结点。

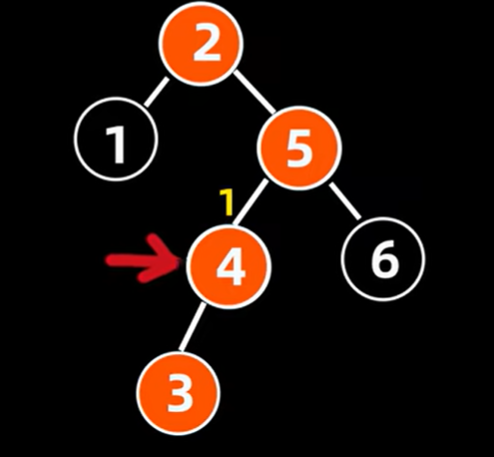
在这里插入图片描述
结果
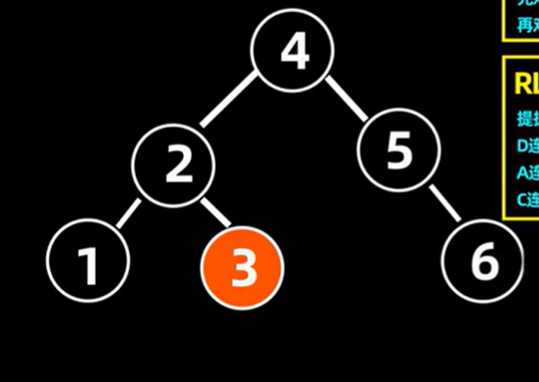
在这里插入图片描述

5.1.7 代码实现

void AVLTree::RotateL(AVLNode*& ptr)
{// 右子树高RR型状态AVLNode* subL = ptr;        // 要旋转的结点，即不平衡的树的根结点ptr = subL->right;              // 原根节点的右结点subL->right = ptr->left;     // 原根子树的右子女转化成其右结点的左子树ptr->left = subL;                 // 把原根节点作为原根节点右结点的左子树，此时ptr为新根节点ptr->bf = subL->bf = 0;}void AVLTree::RotateR(AVLNode*& ptr)
{// 左子树高LL型状态AVLNode* subR = ptr;ptr = subR->left;subR->left = ptr->right;ptr->right = subR;ptr->bf = subR->bf = 0;
}

void AVLTree::RotateRL(AVLNode*& ptr)
{AVLNode* subL = ptr;                // 最后根节点的左子树AVLNode* subR = subL->right;    // 最后根节点的右子树ptr = subR->left;                           subR->left = ptr->right;                // subR的左子树变为其左子女节点的左子女节点ptr->right = subR;                          // 新根节点的右子女结点变为最终右子女结点if (ptr->bf >= 0) subR->bf = 0;else subR->bf = 1;subL->right = ptr->left;                // subL的右子女变为新根节点的左子女结点ptr->left = subL;                           // 新根结点的变为最终的左子女结点if (ptr->bf == 1) subL->bf = -1;else subL->bf = 0;ptr->bf = 0;
}
void AVLTree::RotateLR(AVLNode*& ptr)
{AVLNode* subR = ptr;AVLNode* subL = subR->left;ptr = subL->right;subL->right = ptr->left;ptr->left = subL;if (ptr->bf <= 0) subL->bf = 0;else subL->bf = -1;subR->left = ptr->right;ptr->right = subR;if (ptr->bf = -1) subR->bf = 1;else subR->bf = 0;ptr->bf = 0;
}

5.2 AVL树的插入

沿着其插入路线查各结点的平衡度
各结点会有三种情况
①bf = 0，不需要处理，结束平衡化
②bf = 1，不需要处理，继续回溯
③bf = 2，bf = 2，右子树高，需要结合右子女q的bf做处理
1）q的bf = 1，执行左单旋转，插入位置为RR
2）q的bf=-1，执行先右后左旋转，插入位置为RL
bf=-2，左子树高，需要结合左子女q的bf做处理
1）q的bf=1，执行右单旋转，插入位置为LL
2) q的bf=-1，执行先右旋后左旋，插入位置为LR

bool AVLTree::Insert(AVLNode*& ptr, int& e1)
{AVLNode* pr = NULL;AVLNode* p = ptr;AVLNode* q;int d;Stack st;while (p!=NULL){if (e1 == p->data) return false;        // 找到了e1的结点，不插入pr = p;st.push(pr);                                        // 用栈记录查找路径，并找到插入的父结点prif (e1 < p->data) p = p->left;else p = p->right;}p = new AVLNode(e1);if (p == NULL) { cout << "error when allocate memory!"; exit(1); }if (pr == NULL) { ptr = p; return true; }if (e1 < pr->data) pr->left = p;else pr->right = p;                             // 新结点插入while (st.Isempty() == false) {         // 重新平衡化st.Pop(pr);                                 // 调查父结点的平衡因子 if (p == pr->left) pr->bf--;        // 如果插入左边，则平衡因子-1else pr->bf++;                          // 插入右边则+1，平衡因子高度右边-左边if (pr->bf == 0) break;              // 第一种情况，平衡退出if (pr->bf == 1 || pr->bf == -1)p = pr;                                     // 第二种情况，继续向上搜寻else {                                              // 第三种情况，|bf| =2;d = (pr->bf < 0) ? -1 : 1;          // 区别单双旋if (p->bf == d) {                       // 两节点的平衡因子同号，单旋转if (d == -1) RotateR(pr);       // bf ==-1else RotateL(pr);                   // bf =1}else {if (d == -1) RotateLR(pr);else RotateRL(pr);}break;}if (st.IsEmpty() == true) ptr = pr;     // 调整到树的根节点else {st.getTop(q);if (q->data > pr->data) p->left = pr;else q->right = pr;}}return true;
}

这是>>和<<的重载：

istream& operator>>(istream in, AVLTree& Tree)
{int item;cout << "Construct AVL tree:\n";cout << "Input Data(end with" << Tree.RefValue << "):";in >> item;while (item != Tree.RefValue) {Tree.Insert(item);cout << "Input Data(end with" << Tree.RefValue << "):";in >> item;}return in;
}ostream& operator<<(ostream& out, const AVLTree& Tree)
{out << "Inorder Traversal of AVL tree.\n";Tree.Traverse(Tree.root, out);              // 以中序次序输出个各节点的数据out << endl;return out;
}

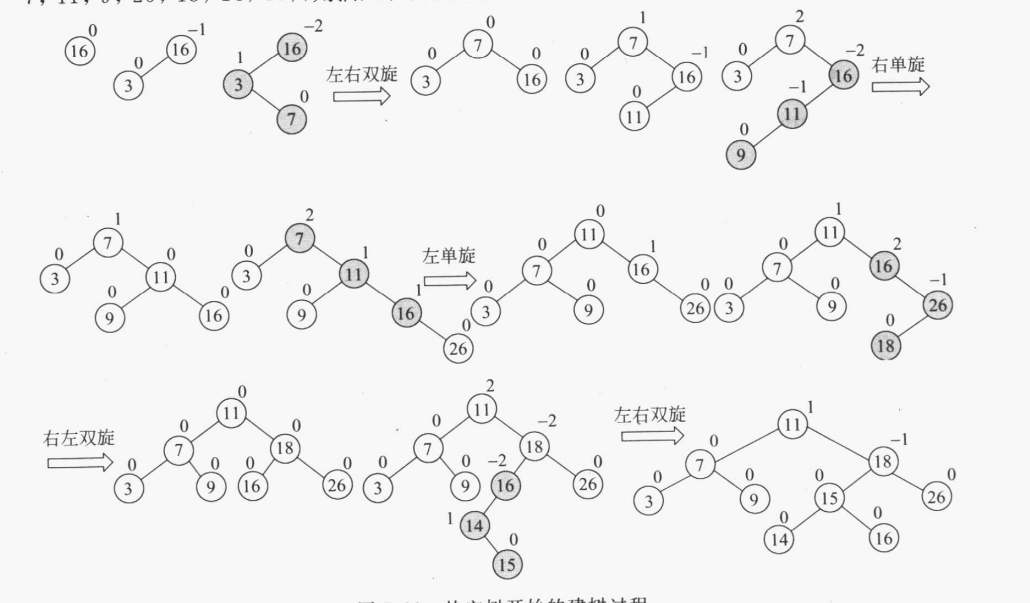
在这里插入图片描述
看懂这个基本就学会了插入了

5.3 AVL树的删除

AVL树的删除算法与二叉搜索树类似，删除后如果破坏平衡性质，还需要做旋转
（1）如果被删结点p有两个子女，p的中序次序下找到直接前驱q，把q的内容传给p，把结点q当作被删结点p，他是只有一个子女的结点，此时看第二种情况
（2）如果被删结点p最多只有一个子女q。可以当p的父结点pr中原来指向p的指针改到q，如果结点p没有子女，p父结点pr的相应指针置位NULL。将原来的结点pr为根的子树的高度-1，并沿pr通向根的路径考量一路上各个结点的影响。
考查结点q的父结点pr。如果q是pr的左子女，则因子bf+1,否则bf-1
此时有三种情况
【1】bf的原来的平衡因子为0，则不需要调整了，结束重新平衡
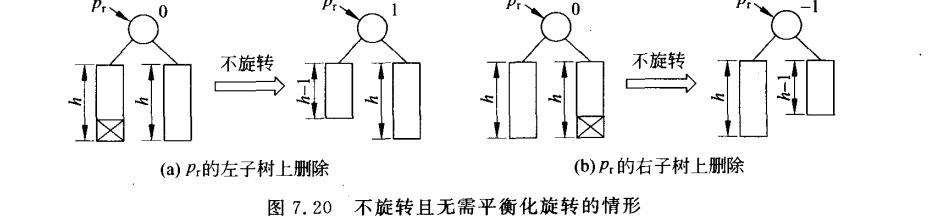
在这里插入图片描述

【2】bf不为0，需要考察结点pr的父结点的平衡状态，
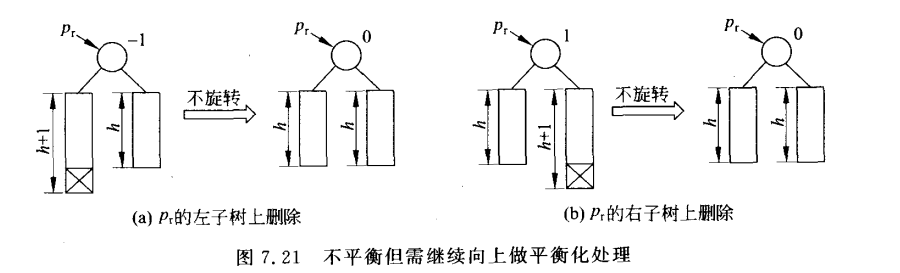
在这里插入图片描述
【3】需要平衡化
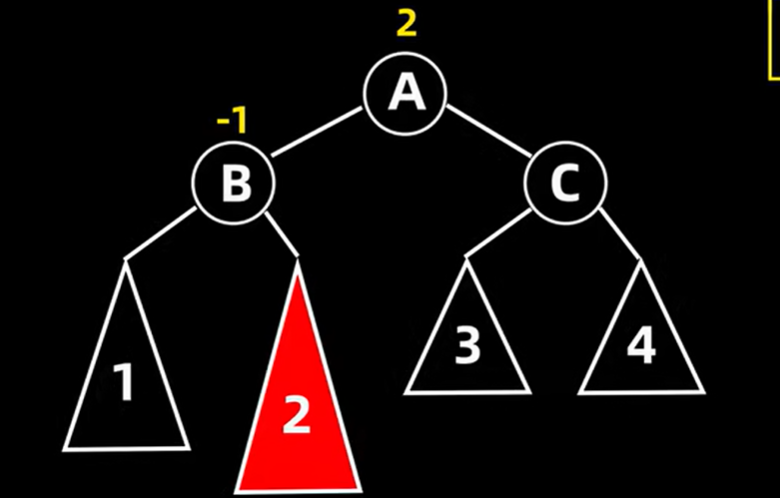
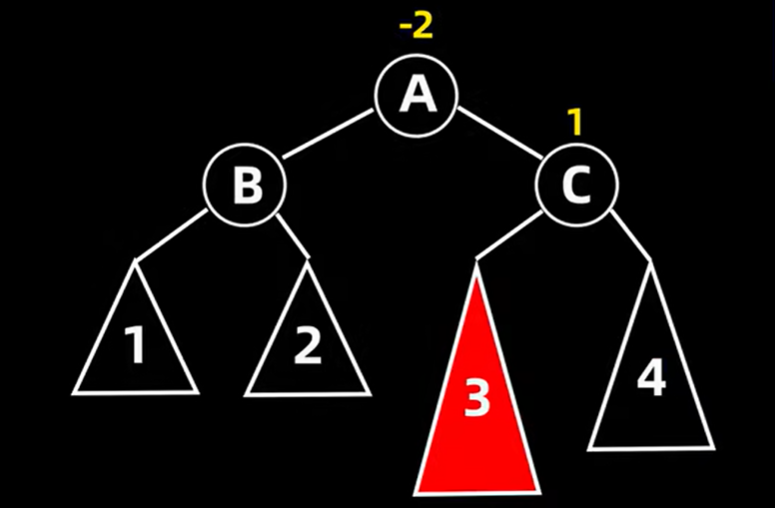
考察父结点pr的更高的子树的根为q（未被缩短的树），根据q的平衡因子，有三种操作
①如果q的平衡因子为0，执行一个单旋（未被缩短的树，结束后可以结束平衡的过程
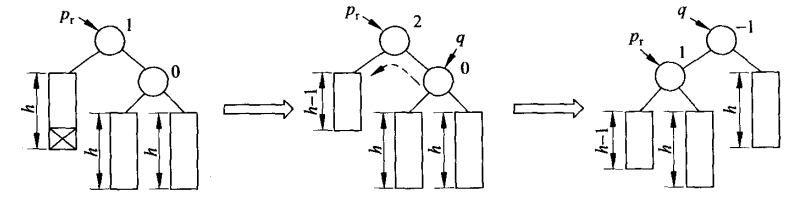
在这里插入图片描述
②如果q的平衡因子与pr的平衡因子正负号相同，则执行一个单旋来恢复，结束后需要沿上继续评估平衡状态，相当LL型和RR型
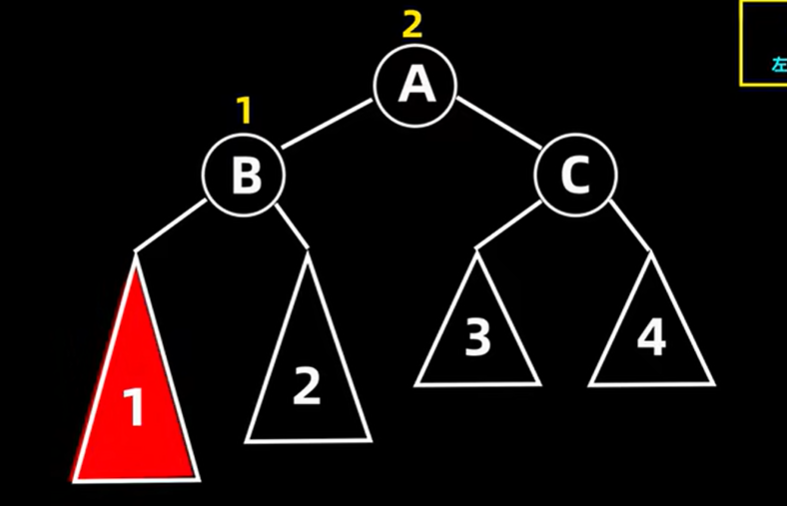
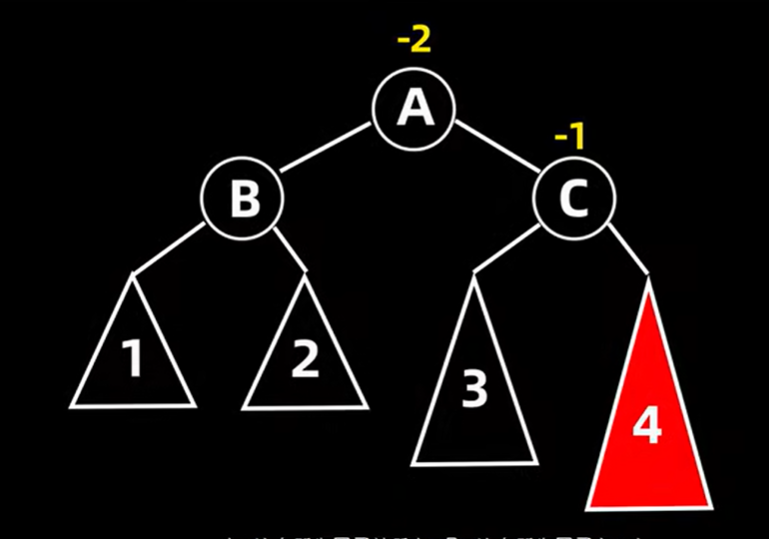
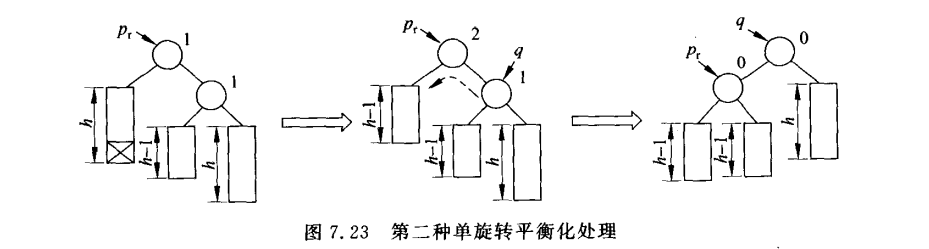
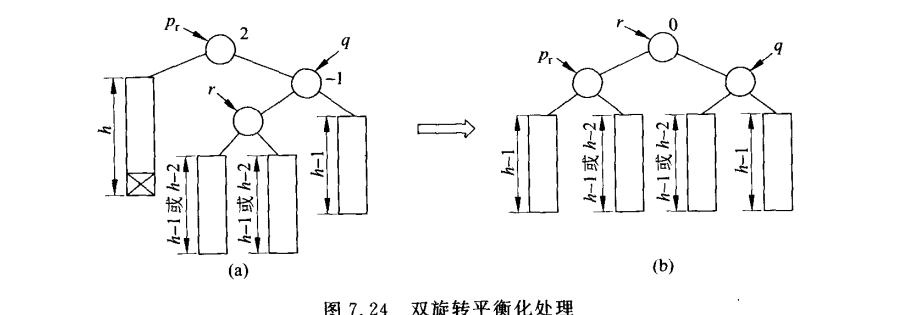
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述
③如果pr与q的平衡因子正负号相反，则需要执行双旋q，相当于LR和RL型，同时继续向上评估
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

bool AVLTree::Remove(AVLNode*& ptr, int x, int& e1)
{// 删除关键码为x的结点AVLNode* pr = NULL;AVLNode *p = ptr;AVLNode* q;AVLNode* ppr;int d;int dd = 0;Stack* st;while (p != NULL) {// 寻找删除位置if (x == p->data) break;pr = p;st.push(pr);if (x < p->data) p = p->left;else p = p->right;}if (p == NULL) return false;            // 未找到，删除if (p->left != NULL && p->right != NULL) {  // 有两各子女的情况pr = p;st.push(pr);q = p->left;                // 再p左子树找到中序遍历直接前驱while (q->right != NULL) {pr = q;st.push(pr); q = q->right;      }p->data = q->data;                  // 用q的值填补pp = q;                                      // 被删结点转为q，此时是只有一个子女结点q的情况}if (p->left != NULL) q = p->left;       // 被删结点只有一个子女else q = p->right;                              // 找到这个子女if (pr == NULL) ptr = q;    // 被删结点为根节点else {                                  // 被删结点不是根节点if (pr->left == p) pr->left = q;        // 把父结点连接到被删结点的子女结点else pr->right = q;while (st.IsEmpty()== false)            // 重新平衡化{st.Pop(pr);             if (pr->right == q) pr->bf--;       // 调整父结点的平衡因子else pr->bf++;if (st.IsEmpty() == false) {st.getTop(ppr);dd = (ppr->left == pr) ? -1 : 1;        // 旋转后和上层连接方向}else dd = 0;                                          // 旋转后不与上层连接if (pr->bf == 1 || pr->bf == -1) break;     // 不需要旋转，直接退出if (pr->bf != 0) {if (pr->bf < 0) { d = -1; q = pr->left; }else { d = 1; q = pr->right; }if (q->bf == 0) {if (d == -1) {RotateR(pr);pr->bf = 1;pr->left->bf = -1;}else {RotateL(pr);pr->bf = -1;pr->right->bf = 1;}break;}if (q->bf == d) {if (d == -1) RotateR(pr);else RotateL(pr);}else {if (d == -1) RotateLR(pr);else RotateRL(pr);}if (dd == -1) ppr->left = pr;else if (dd == 1) ppr->right = pr;}q = pr;}if (st.IsEmpty() == true) ptr = pr;}delete p;return true;
}

不懂这段代码，真的很痛苦看的我

6 伸展树

每次插入结点，所有结点都要调整到根结点。
伸展树

6.1 插入

插入位置为根的左节点，右旋
插入位置为根的右结点，左旋
最左边LL情况，对中间结点进行右旋，在对结点进行右旋，直到变成根节点
最右边RR情况，对中间结点进行左旋，在对结点进行左旋，直到变成根节点
LR情况，中间结点先左旋后右旋，再对结点左旋右旋，直到变为根节点
RL情况，中间结点先右旋后左旋，再对结点右旋左旋，直到变为根节点

6.2 查找

插入和查找操作，查找后把查找到的结点变为根节点，情况跟插入类似

6.3 删除

和二叉搜索树相同，但需要把被删除结点的父结点展开到根节点。

7 红黑树

在这里插入图片描述
1）外部结点是黑色（空指针们
2）没有两个连续结点是红色，（可以两个连续结点是黑色
3）根到外部节点的路径上都有相同的黑色结点
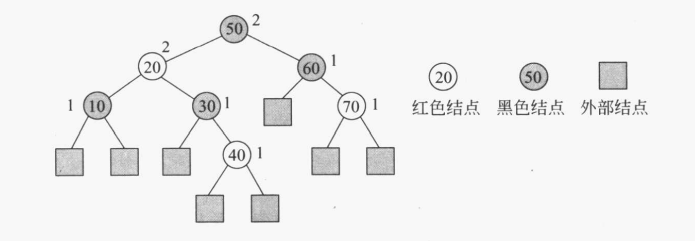
在这里插入图片描述
也可以从指针看
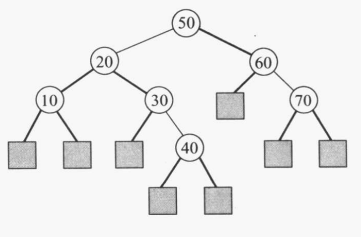
在这里插入图片描述

在这里插入图片描述

7.1 红黑树搜索

和二叉搜索树完全相同

7.2 插入和删除

这个书上标**了，我这边先不学，看了下内容挺多的，后面再补

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/286159.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

OpenHarmony 启动流程优化

OpenHarmony 启动流程优化

目前rk3568的开机时间有21s&#xff0c;统计的是关机后从按下 power 按键到显示锁屏的时间&#xff0c;当对openharmony的系统进行了裁剪子系统&#xff0c;系统app&#xff0c;禁用部分服务后发现开机时间仅仅提高到了20.94s 优化微乎其微。在对init进程的log进行分析并解决其…
阅读更多...
win10系统计算机名称查看及重命名操作方法

win10系统计算机名称查看及重命名操作方法

win10系统计算机名称查看及重命名操作方法 一、在 Windows 10 操作系统中查看计算机的名称步骤二、重命名计算机名称 一、在 Windows 10 操作系统中查看计算机的名称步骤 点击桌面左下角的“开始”按钮&#xff0c;点击“设置”图标&#xff08;齿轮状图标&#xff09;&#x…
阅读更多...
采购审批工作流程快速指南

采购审批工作流程快速指南

对很多人来说&#xff0c;控制每一分钱的支出是一件棘手的事情&#xff0c;但在当下充满不确定性的环境里&#xff0c;这一点与收入增长同等重要。正如俗话说&#xff1a;要想赚钱&#xff0c;先学会花钱。 本文将分析支出控制的基石之一&#xff1a;采购审批工作流程。有了审…
阅读更多...
安防视频云平台/可视化监控云平台EasyCVR获取设备录像失败，该如何解决？

安防视频云平台/可视化监控云平台EasyCVR获取设备录像失败，该如何解决？

视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同&#xff0c;支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。GB28181音视频流媒体视频平台EasyCVR拓展性强&#xff0c;视频能力丰富&#xff0c;具体可实现视频监控直播、视频轮播、视…
阅读更多...
计算机组成原理（存储器与CPU的连接）

计算机组成原理（存储器与CPU的连接）

题目&#xff1a; 设 CPU 共有 16 根地址线。8 根数据线&#xff0c;并用 作访存控制信号&#xff0c;R/作读/写命令信号。现有这些存储芯片:ROM (2K*8 位、4K*4 位、8K*8 位)&#xff0c;RAM(1K*4 位、2K*8 位、4K*8 位)及 74138 译码器和其他门电路(门电路自定)。试从上述规…
阅读更多...
drf入门规范（二）

drf入门规范（二）

四 RESTful API规范 REST全称是Representational State Transfer&#xff0c;中文意思是表述&#xff08;编者注&#xff1a;通常译为表征性状态转移&#xff09;。 它首次出现在2000年Roy Fielding的博士论文中。 RESTful是一种定义Web API接口的设计风格&#xff0c;尤其适用…
阅读更多...
MATLAB2022安装下载教程

MATLAB2022安装下载教程

安装包需从夸克网盘自取&#xff1a; 链接&#xff1a;https://pan.quark.cn/s/373ffc9213a1 提取码&#xff1a;N7PW 1.将安装包解压 2.以管理员的身份运行文件夹中的setup文件 3.点击高级选项--->我有文件安装密钥 4. 选择【是】&#xff0c;进入下一步 5.输入密钥 0532…
阅读更多...
防止被坑！明理信息科技知识服务平台教你如何明智选择知识付费平台

防止被坑！明理信息科技知识服务平台教你如何明智选择知识付费平台

明理信息科技知识服务平台 随着知识经济的兴起&#xff0c;知识付费已经成为一种趋势。越来越多的人开始将自己的知识和技能进行变现&#xff0c;而知识付费小程序平台则成为了一个重要的渠道。然而&#xff0c;市面上的知识付费小程序平台琳琅满目&#xff0c;其中不乏一些不…
阅读更多...
PIC单片机项目（5）——基于PIC16F877A的多功能防盗门

PIC单片机项目（5）——基于PIC16F877A的多功能防盗门

1.功能设计 本次设计的功能如下&#xff1a;如果红外对管检测到有人经过&#xff0c;LCD1602可以显示&#xff0c;我设计的是显示字符串“someone”。 如果有人强行破门&#xff0c;FSR402压力传感器会检测到压力过大&#xff0c;然后触发蜂鸣器报警&#xff0c;LCD1602也显示“…
阅读更多...
11 Flume增量表数据同步配置

11 Flume增量表数据同步配置

增量表数据通道 数据通道如下图所示 Flume 配置 概述 Flume需要将Kafka中topic_db主题的数据传输到HDFS&#xff0c;故其需选用KafkaSource以及HDFSSink&#xff0c;Channel选用FileChannel。 需要注意的是&#xff0c; HDFSSink需要将不同mysql业务表的数据写到不同的路径…
阅读更多...
天锐绿盾行为审计监控管理系统

天锐绿盾行为审计监控管理系统

其工作原理主要是通过在被监控电脑上安装代理程序&#xff0c;实现对该电脑的全方位监控。同时&#xff0c;代理程序会将收集到的数据传输到服务器上&#xff0c;以便管理人员随时查看。 PC访问地址&#xff1a; www.drhchina.com 天锐绿盾监控系统具有以下功能&#xff1a; 能…
阅读更多...
【Spring教程31】SSM框架整合实战：从零开始学习SSM整合配置，如何编写Mybatis SpringMVC JDBC Spring配置类

【Spring教程31】SSM框架整合实战：从零开始学习SSM整合配置，如何编写Mybatis SpringMVC JDBC Spring配置类

目录 1 流程分析2 整合配置2.1 步骤1&#xff1a;创建Maven的web项目2.2 步骤2:添加依赖2.3 步骤3:创建项目包结构2.4 步骤4:创建SpringConfig配置类2.5 步骤5:创建JdbcConfig配置类2.6 步骤6:创建MybatisConfig配置类2.7 步骤7:创建jdbc.properties2.8 步骤8:创建SpringMVC配置…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023