Description
给出一个数据序列,建立二叉排序树,并实现删除功能
对二叉排序树进行中序遍历,可以得到有序的数据序列
Input
第一行输入t,表示有t个数据序列
第二行输入n,表示首个序列包含n个数据
第三行输入n个数据,都是自然数且互不相同,数据之间用空格隔开
第四行输入m,表示要删除m个数据
从第五行起,输入m行,每行一个要删除的数据,都是自然数
以此类推输入下一个示例
Output
第一行输出有序的数据序列,对二叉排序树进行中序遍历可以得到
从第二行起,输出删除第m个数据后的有序序列,输出m行
以此类推输出下一个示例的结果
Sample
Hint
当删除数据不在序列中,那么删除操作等于不执行,所以输出序列不变化
分析:删除的节点有三种情况。
-
叶子节点,即没有左子树和右子树
-
只有右子树或者只有左子树
-
同时有左右子树
思路:
创建deleteNode方法,deleteNode(BinaryTreeNode*& t, int deleteNumber),传入参数为根节点以及删除的值。

值相等之后进行判断
第一个判断:
左子树为空(包含叶子节点的情况,左右子树同时为空,右子树为NULL,temp会保存NULL,最后t被替换成NULL,相当于删除了叶子节点)

第二个判断:
右子树为空,左子树不为空。操作同上

第三个判断:
左右子树都不为空。先找到右子树上最小节点,于是用函数BinaryTreeNode* findMinNode(BinaryTreeNode* t)进行寻找,进入右子树之后,当前节点不存在左子树时即为最小值。t为当前要删除的节点,用右子树上最小节点值替换当前节点值。替换值完成后进入右子树,重新调用deleteNode删除掉右子树最小节点即完成替换。


例如:
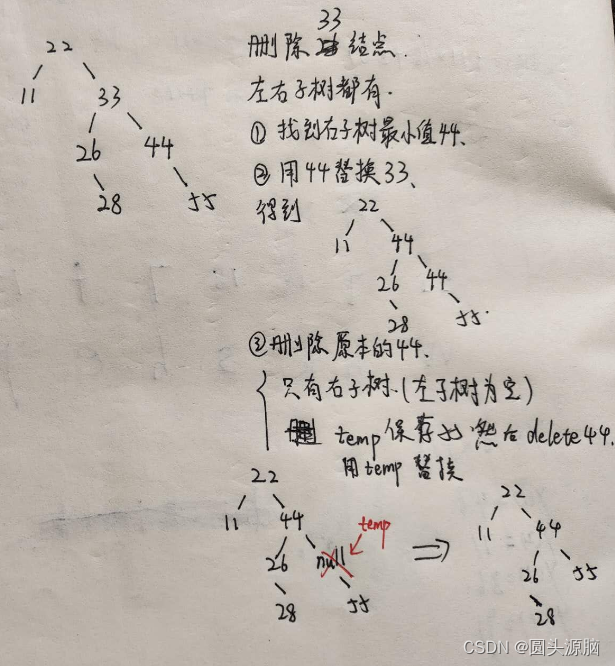
最关键的是要对二叉排序树的性质要熟悉,左子树上所有的值都小于根节点,右子树上所有的值都大于根节点。
AC代码:
#include <iostream>
using namespace std;struct BinaryTreeNode {int data;BinaryTreeNode* left;BinaryTreeNode* right;BinaryTreeNode() {data = 0;left = NULL;right = NULL;}
};class BinaryTree {
public:BinaryTreeNode* root;BinaryTree() {root = nullptr;}~BinaryTree() {destroyTree(root);}void init(BinaryTreeNode*& t, int data) {if (t) {if (data > t->data && t->right) {init(t->right, data);}else if (data < t->data && t->left) {init(t->left, data);}else if (data == t->data) {return;}if (data > t->data && t->right == NULL) {BinaryTreeNode* newNode = new BinaryTreeNode;newNode->data = data;t->right = newNode;}else if (data < t->data && t->left == NULL) {BinaryTreeNode* newNode = new BinaryTreeNode;newNode->data = data;t->left = newNode;}}else {t = new BinaryTreeNode;t->data = data;}}void midTree(BinaryTreeNode* t) {if (t) {midTree(t->left);cout << t->data << " ";midTree(t->right);}}void deleteNode(BinaryTreeNode*& t, int deleteNumber) {if (t == nullptr) {return;}//通过删除值与当前节点值进行比较,进行递归处理,直到值相等。if (deleteNumber > t->data) {deleteNode(t->right, deleteNumber);}else if (deleteNumber < t->data) {deleteNode(t->left, deleteNumber);}else {if (t->left == nullptr) {//左子树为空(包含叶子节点的情况,左右子树同时为空,右子树为NULL,temp会保存NULL,最后t被替换成NULL,相当于删除了叶子节点)BinaryTreeNode* temp = t->right;//临时节点保存右子树delete t;//删除当前节点t = temp;//用右子树替换当前节点}else if (t->right == nullptr) {//右子树为空,左子树不为空。操作同上BinaryTreeNode* temp = t->left;delete t;t = temp;}else {//左右子树都不为空。//找到右子树上最小节点BinaryTreeNode* minNode = findMinNode(t->right);//t为当前要删除的节点,用右子树上最小节点值替换当前节点值。t->data = minNode->data;deleteNode(t->right, minNode->data);//然后进入右子树,删除掉右子树最小节点即完成替换。}}}BinaryTreeNode* findMinNode(BinaryTreeNode* t) {while (t->left != nullptr) {t = t->left;}return t;}void destroyTree(BinaryTreeNode* t) {if (t) {destroyTree(t->left);destroyTree(t->right);delete t;}}
};int main() {int t;cin >> t;while (t--) {int n;cin >> n;BinaryTree p;while (n--) {int data;cin >> data;p.init(p.root, data);}p.midTree(p.root);cout << endl;int deleteTimes;cin >> deleteTimes;while (deleteTimes--) {int deleteNum;cin >> deleteNum;p.deleteNode(p.root, deleteNum);p.midTree(p.root);cout << endl;}}
}