非线性弹簧摆的仿真（Matlab代码实现）-编程知识

非线性弹簧摆的仿真（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

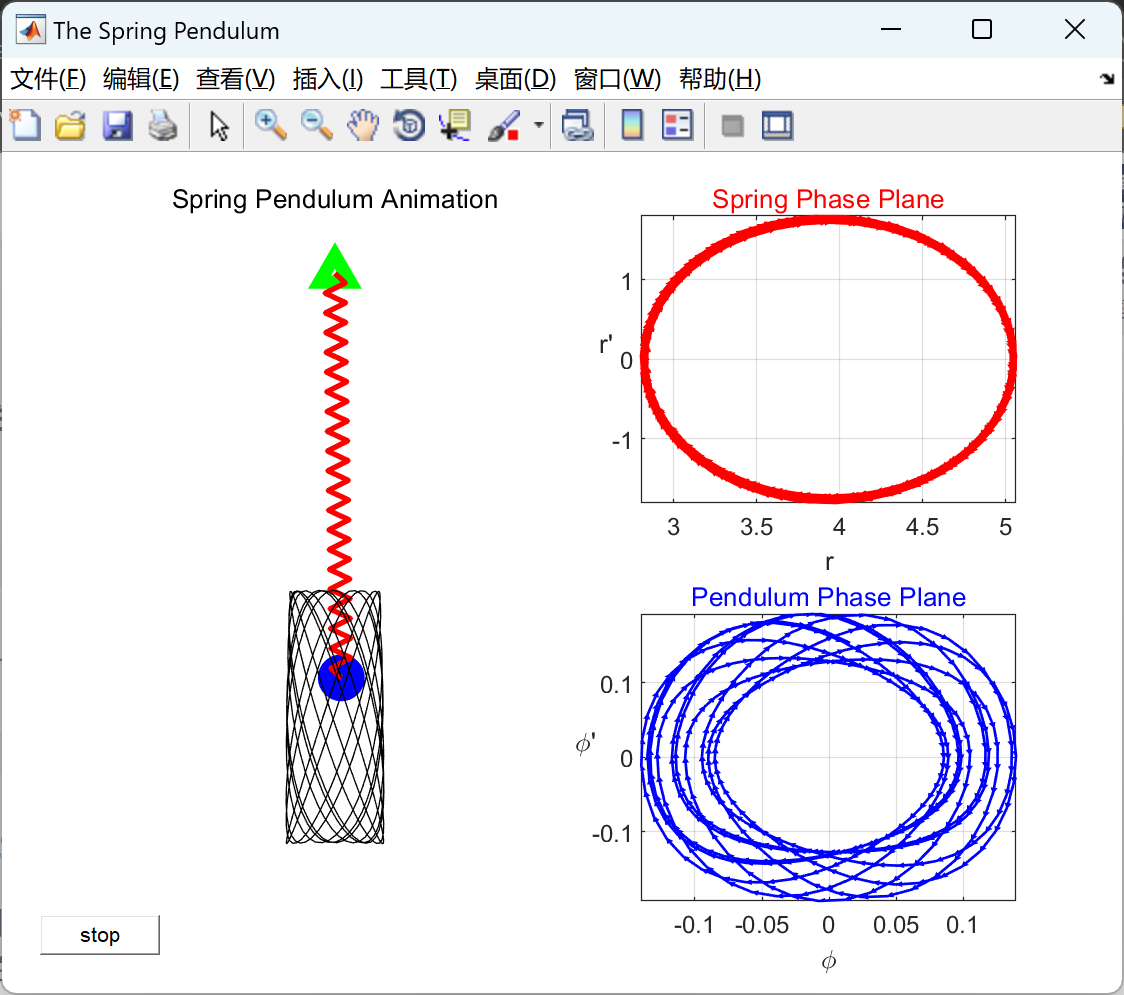
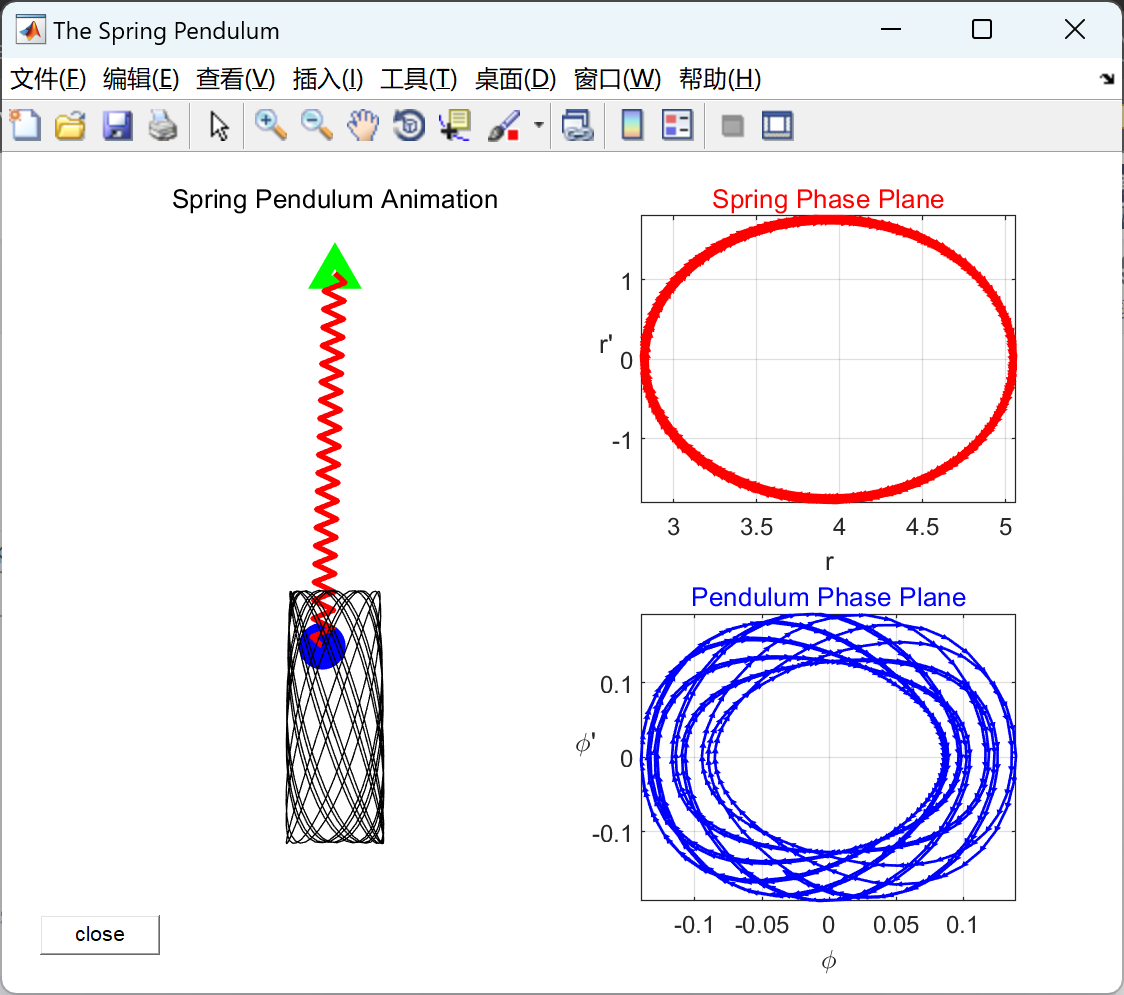
本文模拟非线性弹簧摆。弹簧运动和摆锤运动的相平面图将相应更新。摆方程是非线性的，使用 MATLAB 的 ode45 求解。摆锤的质量、长度和持续时间以及初始值可以根据要求进行更改。

非线性弹簧摆是一个简单而有趣的系统，可以用于展示非线性动力学行为。以下是一种仿真非线性弹簧摆的方法：

1. 定义系统：首先定义非线性弹簧摆的系统参数，如质量、摆长、初始角度等。同时明确使用的非线性弹簧力学模型，可以是简单的非线性刚度关系或更复杂的非线性力学模型。

2. 建立动力学模型：基于系统的几何和力学关系，建立非线性弹簧摆的动力学模型。可以使用拉格朗日方程或欧拉-拉格朗日方程等方法推导出系统的运动方程。

3. 数值求解：使用数值方法（如欧拉法、龙格-库塔法等）对非线性摆的运动方程进行求解。在每个时间步长中，根据当前状态和非线性力学模型计算出下一个时间步长的状态。

4. 模拟运动：根据数值求解的结果，模拟非线性弹簧摆的运动。可以绘制摆角随时间的变化曲线，或者使用动画形式展示摆的运动过程。

在模拟非线性弹簧摆的过程中，你可以尝试不同的初始条件、非线性力学模型以及数值求解方法，观察它们对系统响应的影响。这样可以更好地理解非线性动力学系统的特性，例如摆角的周期性、分岔现象等。

如果你有具体的系统参数和非线性力学模型，可以使用数值计算软件（如MATLAB、Python的NumPy和SciPy库等）编写仿真程序进行模拟。另外，还可以考虑使用动力学仿真软件（如Simulink、OpenModelica等），它们提供了更直观的界面和建模工具，便于进行非线性弹簧摆的仿真和可视化。

📚2 运行结果

非线性弹簧摆的仿真（Matlab代码实现）

非线性弹簧摆的仿真（Matlab代码实现）_哔哩哔哩_bilibili

主函数代码：

clear ;clc ;
% Properties of Pendulum (Can be altered)
g = 9.81 ; % Acceleration due to gravity
M = 2 ; % Mass of the pendulum
L = 1 ; % Length of the Pendulum
K = 5 ; % Spring Constant
% Initial Boundary Conditions (Can be altered)
r = 3 ; % Extension Length
rdot = 1. ;
Phi = 0.1 ; % Position
Phidot = 0.1; % Velocity

duration = 60; % Duration of the Simulation
fps = 10; % Frames per second
%movie = true; % true if wanted to save animation as avi file
movie = false ; % false if only want to view animation
arrow = true ; % Shows the direction of phase plane plot
%arrow = false ; % Will not show the direction of phase plane plot
interval = [0, duration]; % Time span
ivp=[r ;rdot ;Phi ;Phidot ;g ;M ;L ; K]; % Initial value's for the problem
% Simulation of Simple Pendulum
Animation(ivp,duration,fps,movie,arrow);