数据结构和算法-红黑树（定义性质查找插入删除）-编程知识

数据结构和算法-红黑树（定义性质查找插入删除）

文章目录

红黑树的定义和性质
- 为什么要发明红黑树？
- 红黑树怎么考
- 总览
- 红黑树的定义
- - 实例：一颗红黑树
  - 练习：是否符合红黑树的要求
  - 一种可能的出题思路
  - 补充概念：节点黑高
- 红黑树的性质
红黑树的查找
红黑树的插入
- 实例
- 小结
- 与黑高相关的理论
红黑树的删除

红黑树的定义和性质

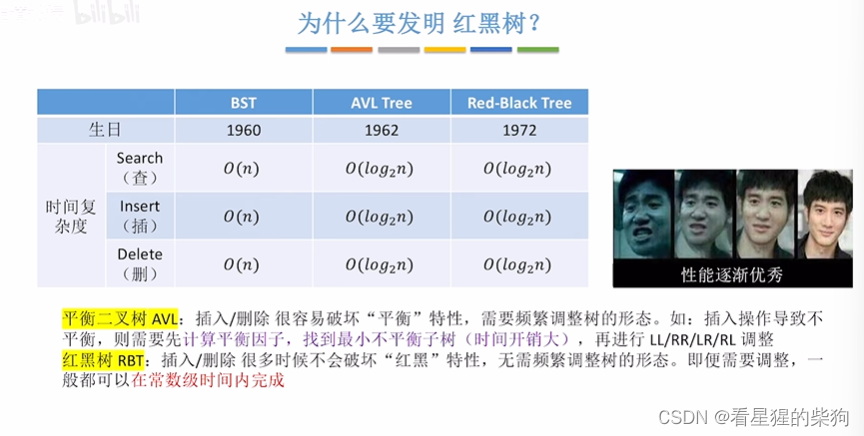
为什么要发明红黑树？

插入和删除即一般不会破坏特性，并且即使破坏，恢复的代价比较低
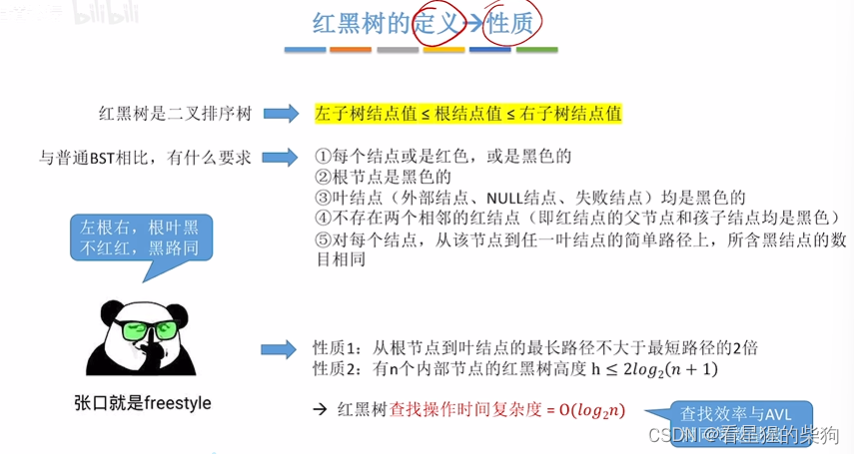
在这里插入图片描述

红黑树怎么考

在这里插入图片描述

总览

在这里插入图片描述

红黑树的定义

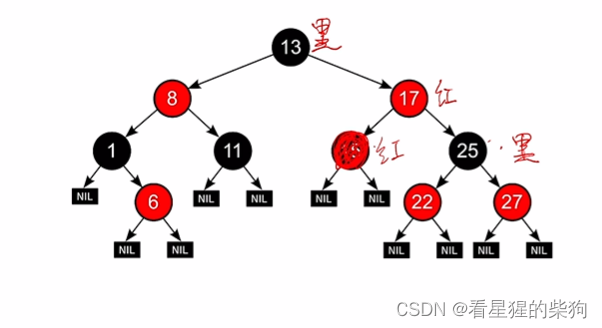
叶节点不是我们认为的没有子树的节点了，是空节点，即我们所认识的叶子节点的孩子就是叶节点
在这里插入图片描述

实例：一颗红黑树

在这里插入图片描述

练习：是否符合红黑树的要求

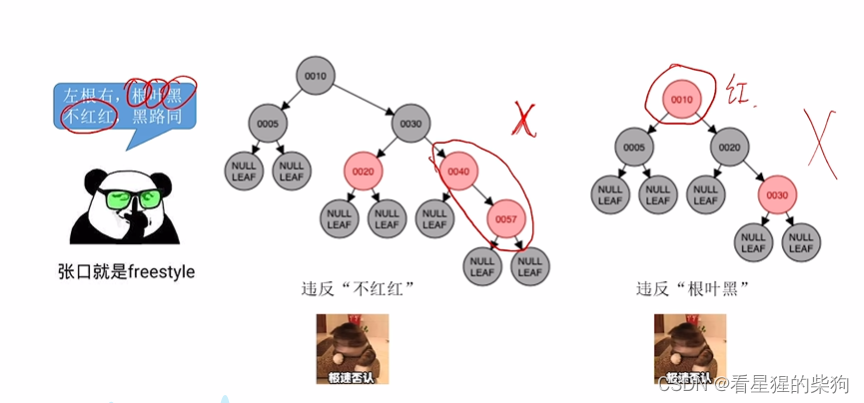
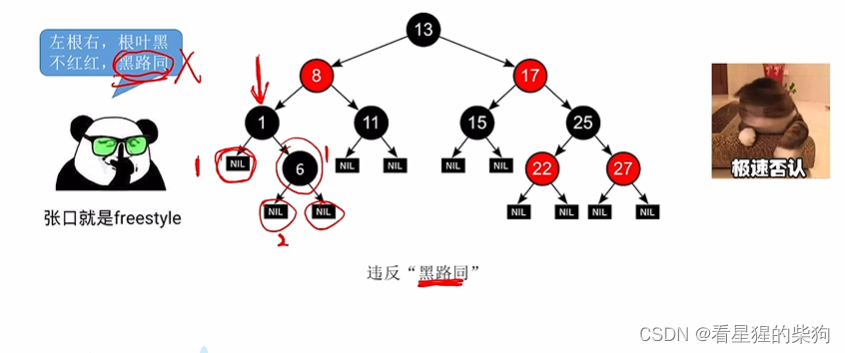
在这里插入图片描述

将6变为红后

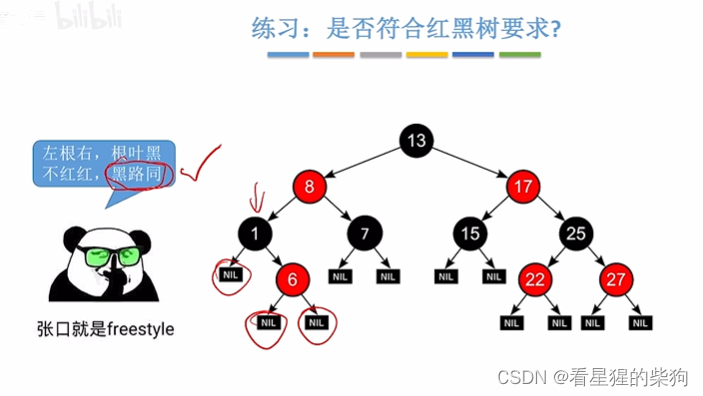
但此时7不满足二叉排序树，替换为11即可

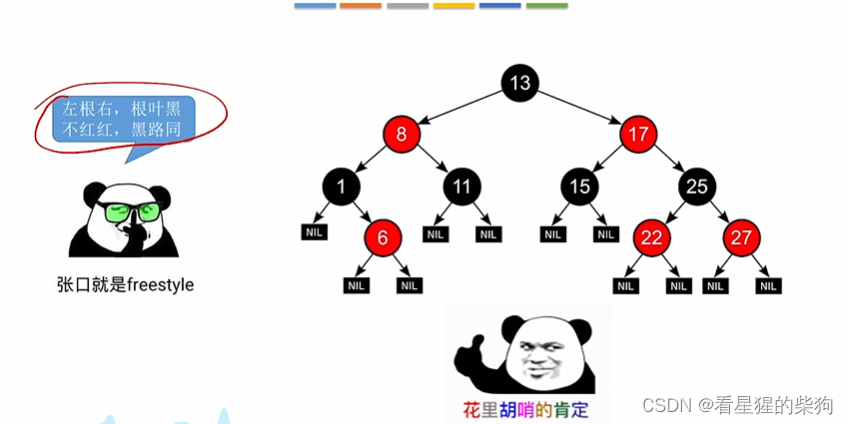
一种可能的出题思路

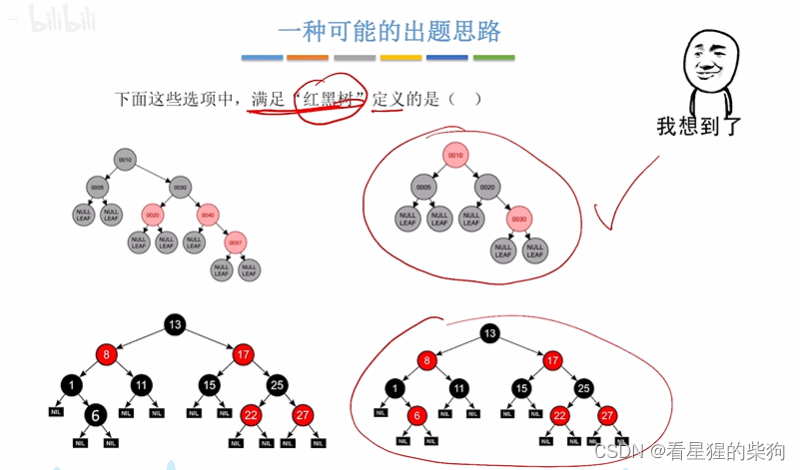
在这里插入图片描述

补充概念：节点黑高

注意不包括出发的节点
在这里插入图片描述

红黑树的性质

由于根节点到任意节点的的路径上所含黑节点的数目相同，最短就是全黑嘛，但最长就是有红节点在路径上，由于不存在相邻的红节点这个特性，所以节点树最多的情况就是在黑节点之间有红节点，此时总结点数模至多为全黑节点的两倍
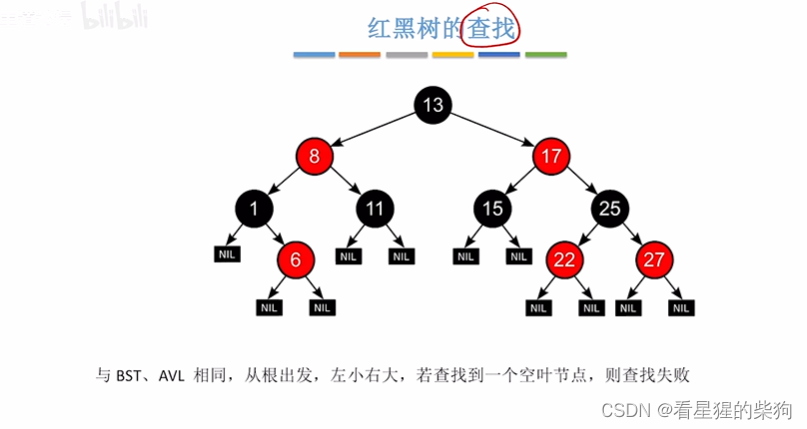
在这里插入图片描述

红黑树的查找

和查找平衡二叉树和二叉排序树一样，小于走左子树，大于走右子树
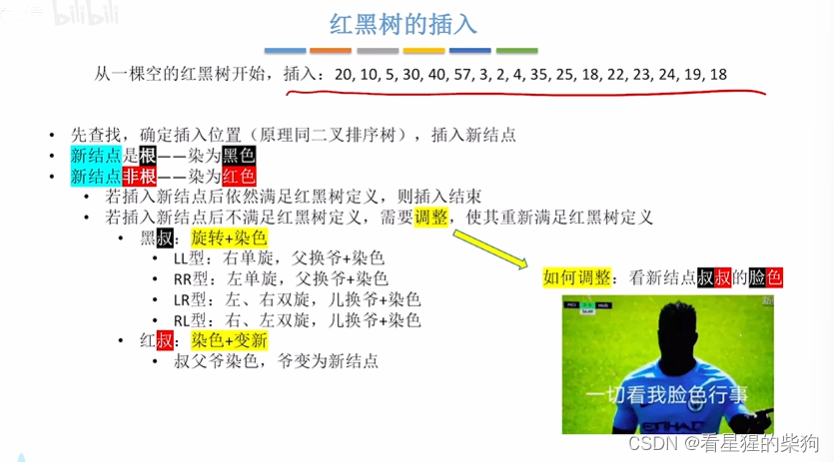
在这里插入图片描述

红黑树的插入

在这里插入图片描述

实例

非根节点的插入只需关注不红红的这个问题

插入非根节点为红是为了保持黑路同
插入5后发现有红红，此时叔节点为黑，相对爷节点是LL型，此时父节点右旋换爷节点同时变色
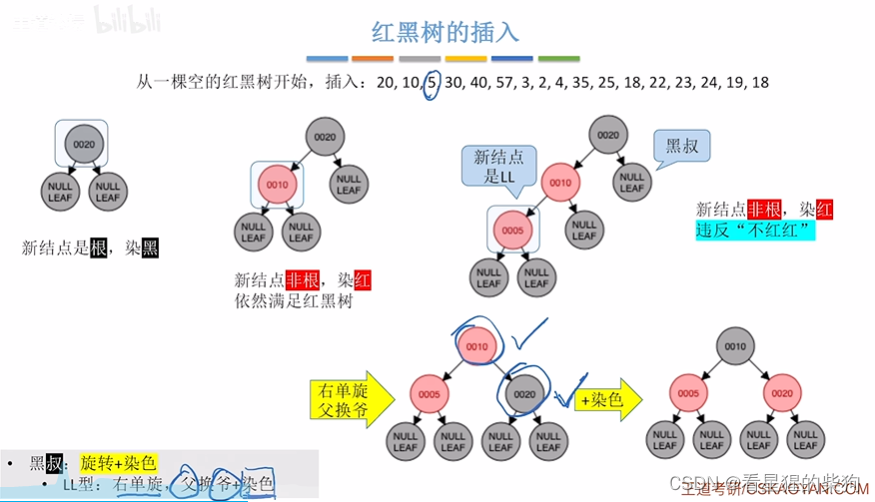
在这里插入图片描述
插入后红红，此时叔为红，此时叔父爷变色，爷看作新节点，，此时爷节点是根但为红色再变色

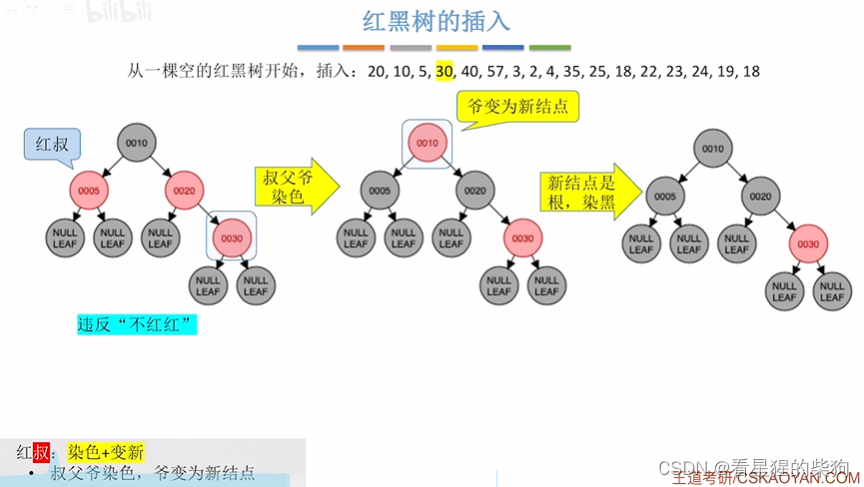
此时再插入一个，存在红红，此时叔为黑，且为RR,此时父换爷，同时父和爷变色

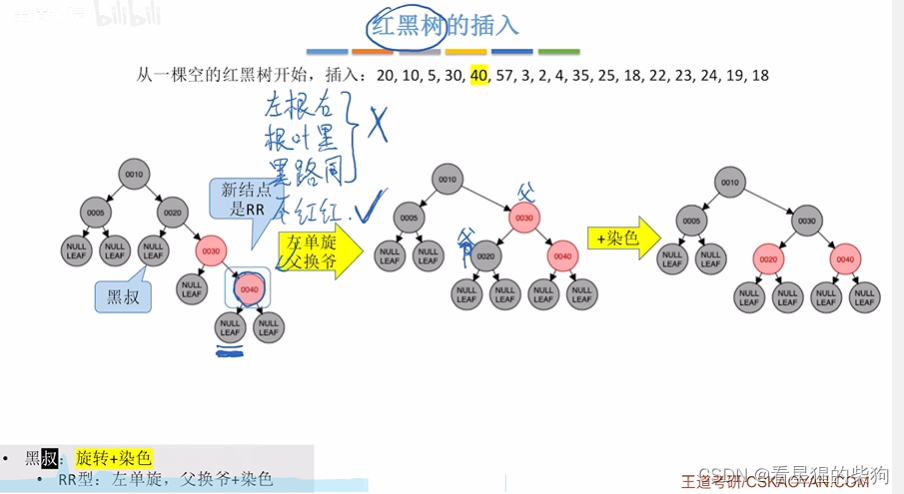
此时加入节点，存在红红，且叔为红，此时叔父爷变色，同时将爷看作新加入的节点，发现没破坏红黑树的特性
在这里插入图片描述
插入3没啥大问题

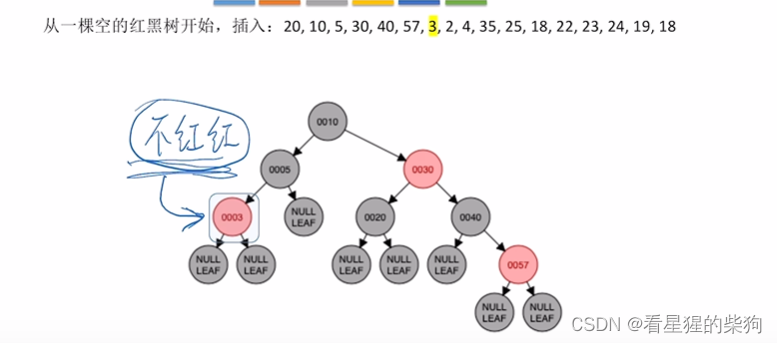
在这里插入图片描述
插入2，此时红红，同样父换爷，同时染色

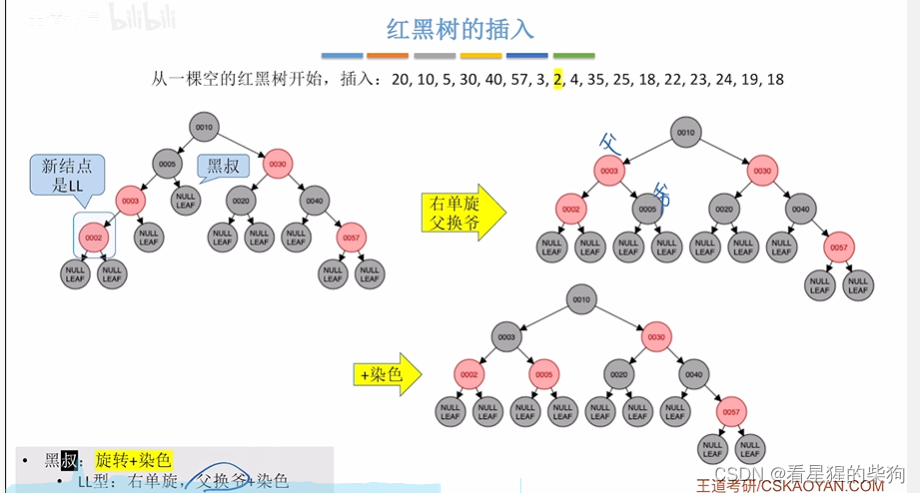
在这里插入图片描述
此时红叔，叔父爷变色，同时爷看作新节点

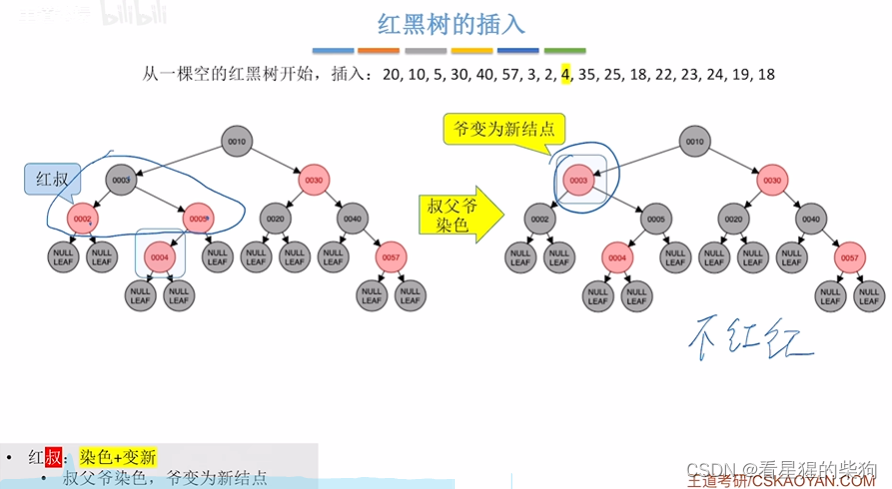
插入35

插入25

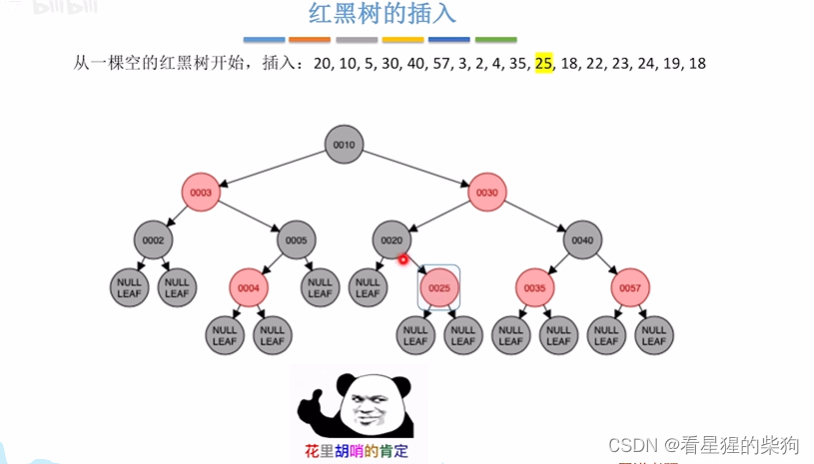
在这里插入图片描述
插入18

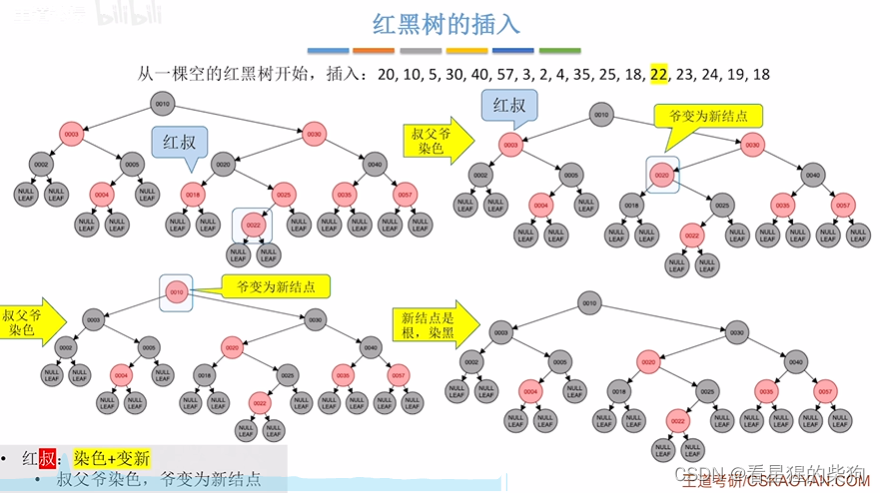
插入22
红红，叔为红，叔父爷变色，此时将爷看作新节点，此时存在红红，而该新节点叔为红，所以此时叔父爷都变色，此时的爷看作新节点，但为红节点，所以变黑

在这里插入图片描述
插入23，此时红红，叔为黑，且为LR，此时左旋再右旋，最后变色

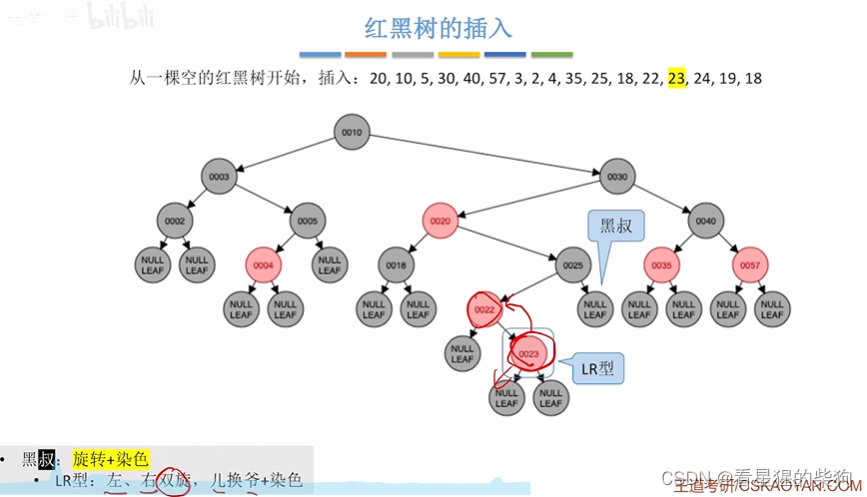
在这里插入图片描述
左旋结果

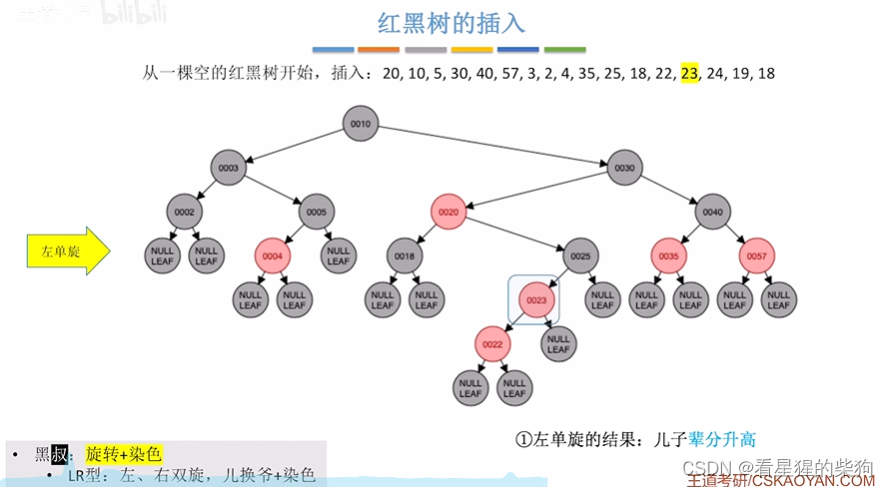
右旋结果

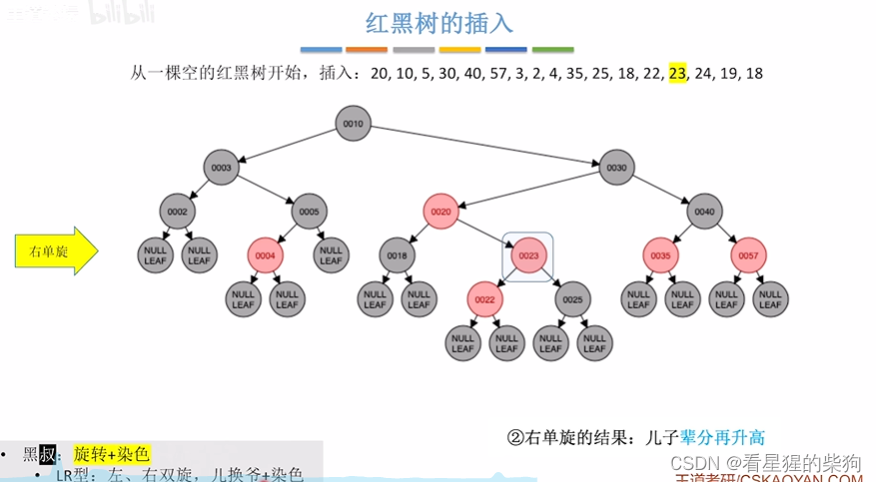
在这里插入图片描述
最后将原来的儿爷节点变色

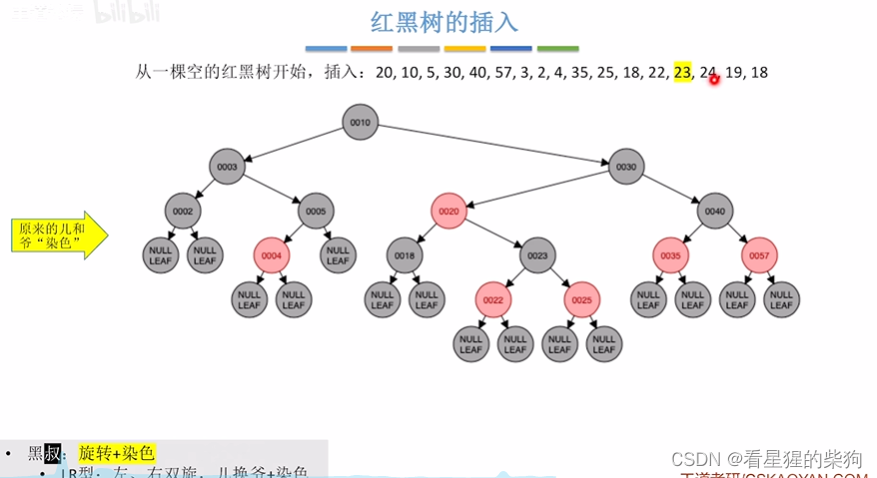
在这里插入图片描述
插入24
红红，此时叔父爷变色，爷看作新节点，存在红红
此时叔为黑，为LR

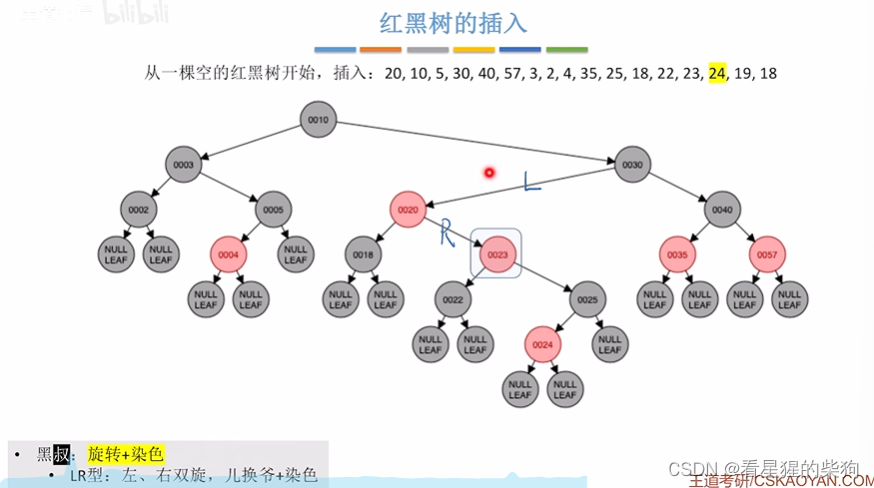
先左旋

再右旋

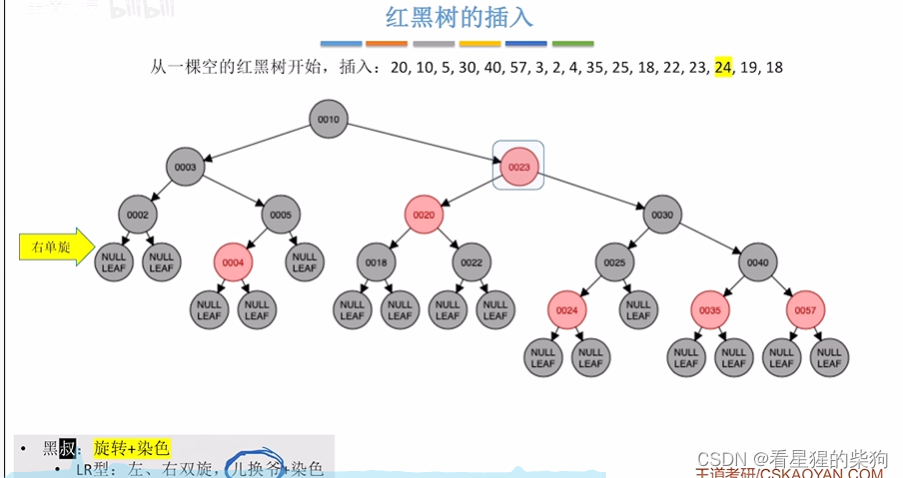
原本的儿爷变色

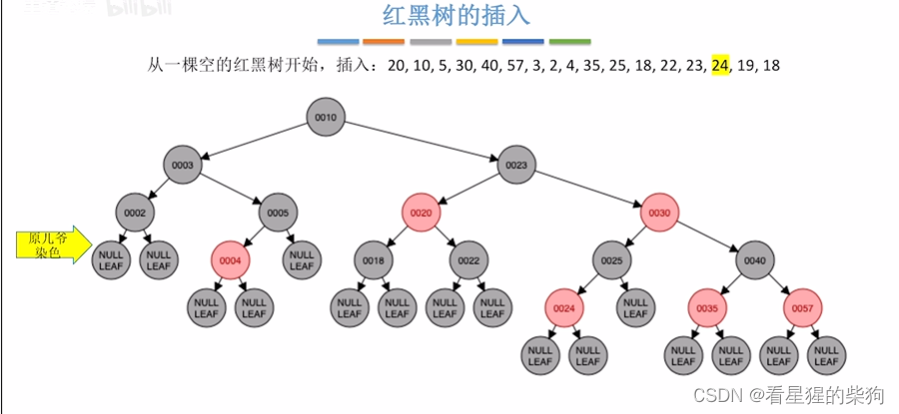
插入19

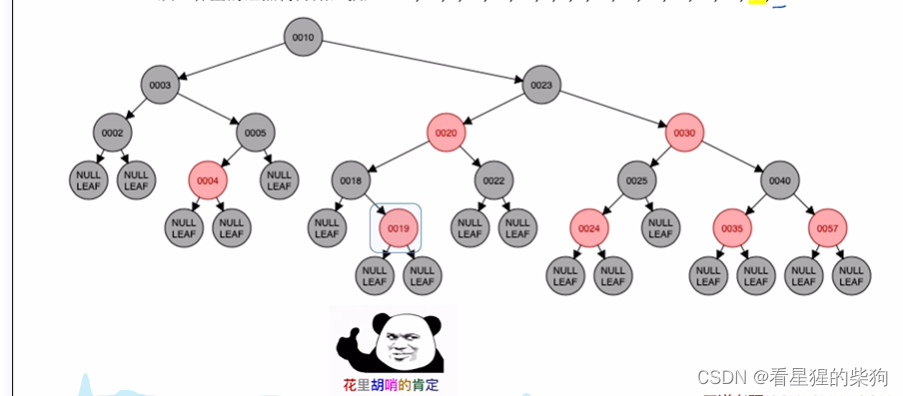
插入18
此时已经存在18，可以放18的左边也可以放右边

若插入右边
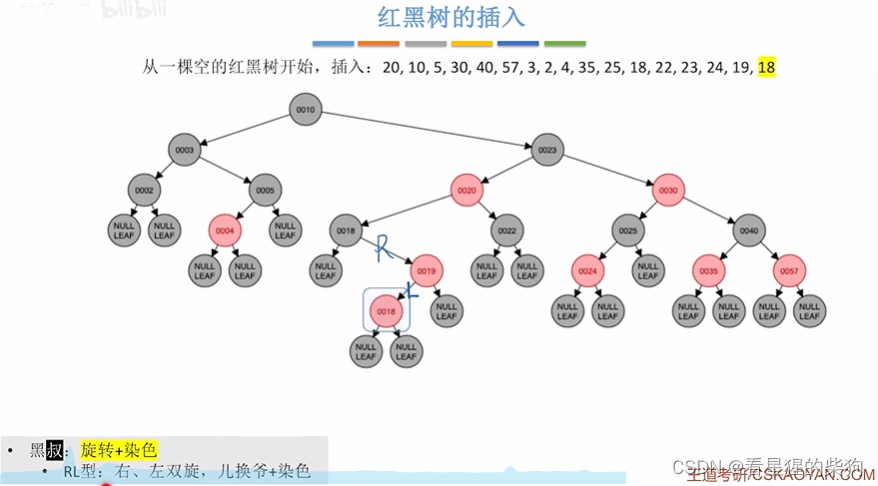
在这里插入图片描述
先右旋

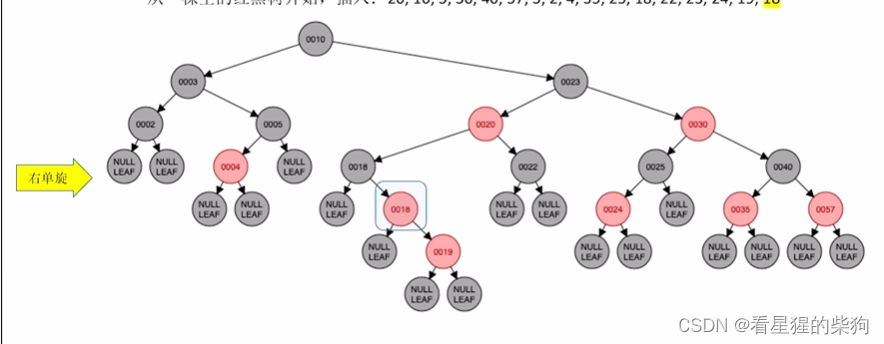
再左旋

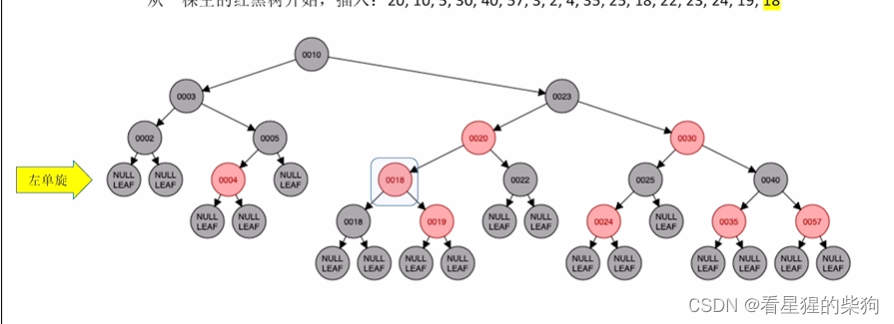
在这里插入图片描述
原本儿爷变色

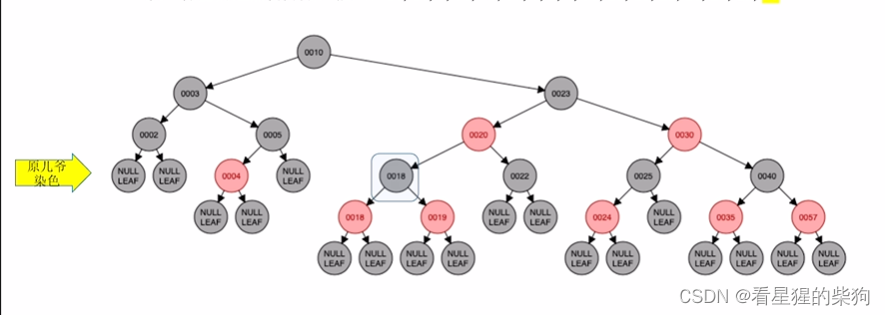
在这里插入图片描述

小结

由根节点到叶节点的最长路径不大于最短路径的两倍可知道左右子树的高度也不过两倍关系
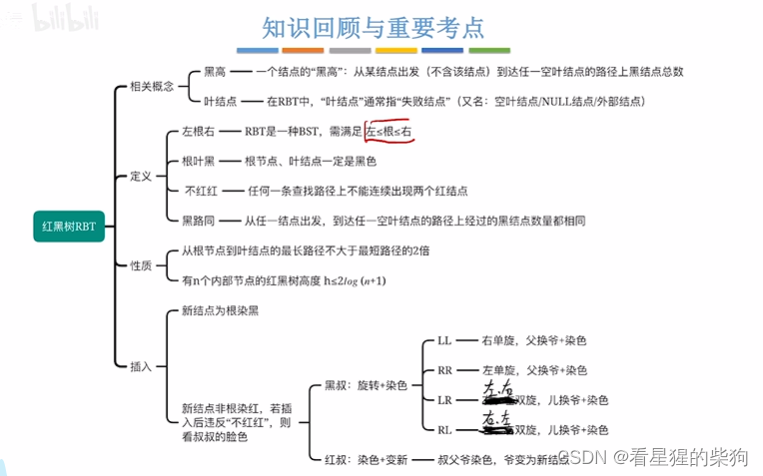
在这里插入图片描述

与黑高相关的理论

外部节点就是空节点
根节点黑高为h的红黑树，此时内部节点要最少的话，必须即全黑即可，因为有红的话不能有相邻的。而此时全黑的情况下也是吗，满树，不然达不到从根节点的黑高为h
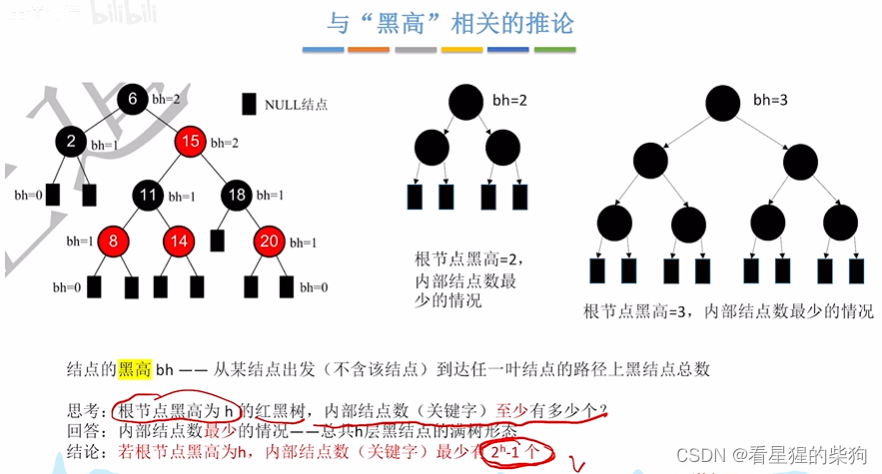
在这里插入图片描述
黑高大于等于h/2是由于如果是一个黑一红那么黑高将大于等于h/2，又由根节点黑高可得出内部节点数最少数量，最后可得出总高度的范围