题意理解：

        气球用一个闭区间表示，击中区间内任意一个位置，气球会被引爆。

        区间指示了气球的位置和气球的可射击范围。

        若两个气球位置有重叠，则一只箭能解决引爆两个气球。

        目标：尽可能射击气球重叠最多的位置，用最少的箭引爆所有气球。

解题思路：

        采用贪心思想来解题，全局最优是用最少的箭引爆最多的气球，

        则局部最优：尽可能射击气球重叠最多的地方。

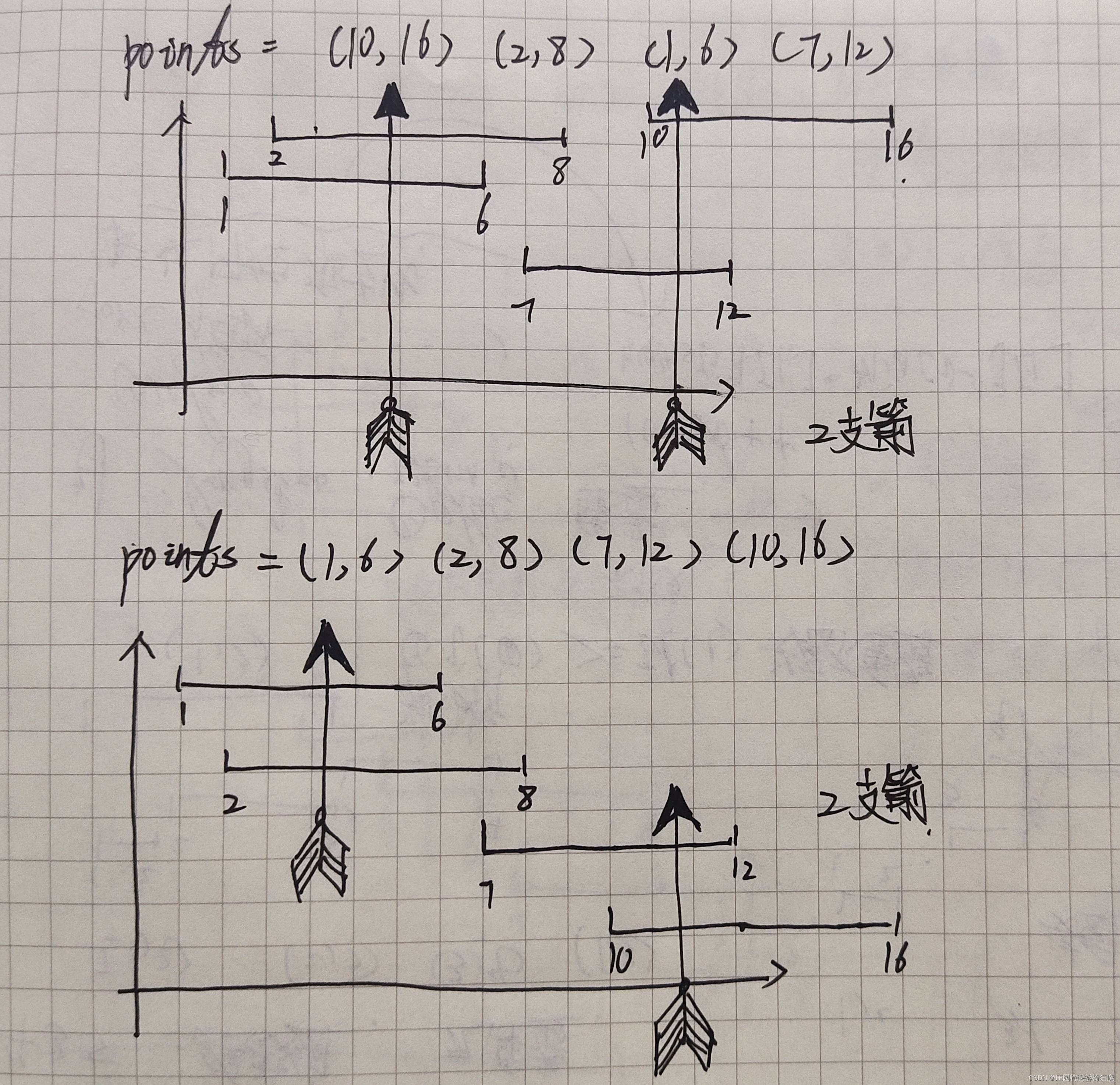
        为了实现局部最优，我们需要对气球的重叠部分进行判断，为了简单进行判断，我们以左区间为标准从小到大进行排序。

        当第i个区间的左边界<=第i-1个区间的右边界时，——两个气球重叠。一只箭可以引爆两个气球。 为了尽可能爆掉最多的气球，尽可能从重叠边缘的最右边射击，以确保爆掉最多的气球。

        所以第i+1个区间的左边界需要和重叠区域的最右边界比较，若重叠，则进行下一个气球的判断，否则，增加一只箭。

        当第i个区间的左边界>第i-1个区间的右边界时，——两个气球不重叠。需要增加一只箭引爆第i个气球。 

1.贪心解题

注意：这里的输入限制如下所示，可能造成溢出，所以推荐使用Integer.comparen比较方法可以防止这个问题。

        在日常解题过程中也推荐有限选择有现有类内置的一些方法。

public int findMinArrowShots(int[][] points) {if(points.length==0) return 0;//记录箭数int count=1;//对point左边界升序排序// 使用Integer内置比较方法，不会溢出Arrays.sort(points, (a, b) -> Integer.compare(a[0], b[0]));//与左边的气球比较for(int i=1;i<points.length;i++){if(points[i][0]<=points[i-1][1]){//有重叠points[i][1]=Math.min(points[i][1],points[i-1][1]);}else{count++;//不重叠，增加一只箭}}return count;}

2.分析

时间复杂度：O(nlogn) 遍历气球的时间O(n)+排序的时间O(nlogn)

空间复杂度：O(logn) 排序所需的栈空间

n为输入数组大小