1. 按摩师

原题链接

---

题干：

按摩师每次预约服务之间要休息
不能接受相邻的预约
给一个请求序列，摘到最优的预约集合，返回总分钟数

算法原理：（dp）

1. 状态表示：

dp[i] 表示：选择到 i 位置的时候，此时的最长预约时长

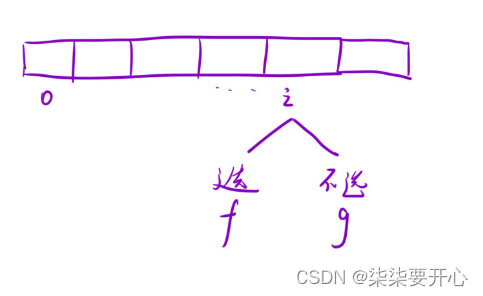
继续细化：
f[i] 表示：选择到 i 位置时， nums[i] 必选，此时的最⻓预约时长
g[i] 表示：选择到 i 位置时， nums[i] 不选，此时的最长预约时长

2. 状态转移方程

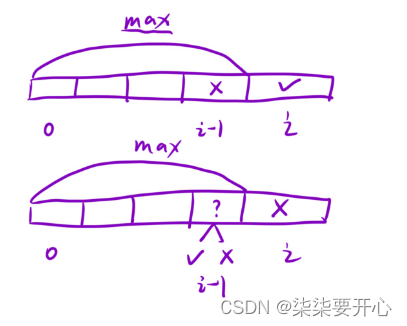
f[i] ：
如果 nums[i] 必选，那么我们仅需知道 i - 1 位置在不选的情况下的最⻓预约时长
然后加上 nums[i] 即可
因此 f[i] = g[i - 1] + nums[i]

g[i] ：
如果 nums[i] 不选，那么 i - 1 位置上选或者不选都可以
因此，我们需要知道 i- 1 位置上选或者不选两种情况下的最长时长
因此 g[i] = max(f[i - 1], g[i- 1])

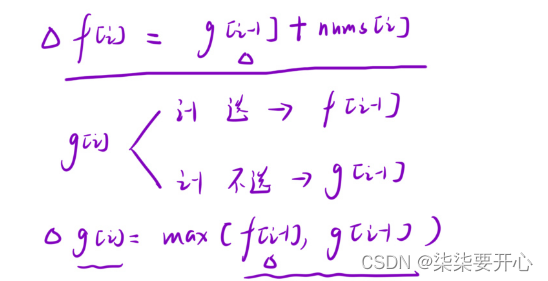
3. 初始化

f[0] = nums[0]
g[0] = 0

4. 填表顺序

从左往右，两个表⼀起填

5. 返回值

max(f[n - 1], g[n - 1])

---

代码：

class Solution {public int massage(int[] nums) {int n = nums.length;if(n == 0) {return 0;}int[] f = new int[n];int[] g = new int[n];f[0] = nums[0];for(int i = 1; i < n; i++) {f[i] = g[i-1] + nums[i];g[i] = Math.max(g[i-1],f[i-1]);}return Math.max(f[n - 1],g[n - 1]);}
}

---

2. 寻找数组的中心下标

原题链接

---

题干：

中心下标：左侧元素和 = 右侧元素和
如果这个值在最左 或者 最右 和为0
有多个下标，返回最左边
不存在这个值，返回 -1

---

算法原理：（前缀和）

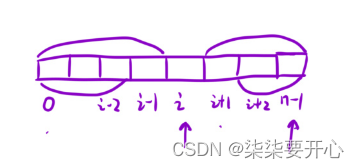
（1）预处理前缀和
f：前缀和数组
f[i] 表示：[0，i-1] 区间，所有元素的和
f[i] = f[i-1] + nums[i-1]

g：后缀和数组
g[i] 表示：[i+1，n-1] 区间，所有元素的和
g[i] = g[i+1] + nums[i+1]

（2）使用前缀和
在 0~n - 1 枚举下标 i
判断 f[i] = g[i]

（3）细节问题
f(0)，g(0) 可能越界访问，需要初始化
f(0) = 0
g(n-1) = 0

（4）填表顺序
f：从左往右
g：从右往左

---

代码：

class Solution {public int pivotIndex(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];for(int i = 1; i < n; i++) {f[i] = f[i - 1] + nums[i - 1];}for(int i = n - 2; i >= 0; i--) {g[i] = g[i + 1] + nums[i + 1];}for(int i = 0; i < n; i++) {if(f[i] == g[i]) {return i;}}return -1;}
}

3. 除自身以外数组的乘积

原题链接

---

题干：

nswer[i]等于nums中 nums[i] 之外其余各元素的乘积
前缀元素和后缀的乘积都在 32位 整数范围

---

算法原理：（前缀和）

（1）预处理前缀积
f：前缀积数组
f[i] 表示：[0，i-1] 区间，所有元素的乘积
f[i] = f[i-1] * nums[i-1]

g：后缀积数组
g[i] 表示：[i+1，n-1] 区间，所有元素的乘积
g[i] = g[i+1] * nums[i+1]

（2）使用前缀和

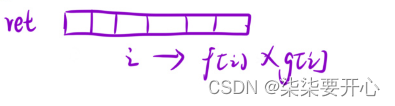
ret[i[i] = f[i] * g[i]

（3）细节问题
f(0) = 1
g(n-1) = 1

（4）填表顺序
f：从左往右
g：从右往左

---

代码：

class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] f = new int[n];int[] g = new int[n];f[0] = g[n-1] = 1;for(int i = 1; i < n; i++) {f[i] = f[i-1] * nums[i-1];}for(int i = n - 2 ; i >= 0; i--) {g[i] = g[i+1] * nums[i+1];}int[] ret = new int[n];for(int i = 0; i < n; i++) {ret[i] = f[i] * g[i];}return ret;}
}