priority_queue的基本介绍

这个priority_queue翻译成中文就是优先级队列，但其实我们很难去一眼看出他的意思到底是什么，他的逻辑结构实际上类似于数据结构中的堆(heap)，而且是大根堆，即为堆顶为序列的最大值

堆(heap)

堆实际上是一种特殊的二叉树，他最最特殊的点在于可以用数组来存储数据

普通的二叉树是不适合用数组来存储的因为可能会存在大量的空间浪费，而对于完全二叉树更适合用顺序结构存储

堆的概念与结构

学术化的定义堆的概念过于难以理解，我们形象化的来理解他

一棵完全二叉树，他的任意一个节点值总是不大于或者不小于他的父节点的值

若堆顶为最大元素，则称为大根堆，若堆顶为最小元素，则称为小根堆

我们可以按照层次遍历的顺序对二叉树的所有节点进行标号，我们可以发现

$ parent = (child -1) / 2$

$child=parent\ast 2+1$

因此我们可以把它放入数组中，例如

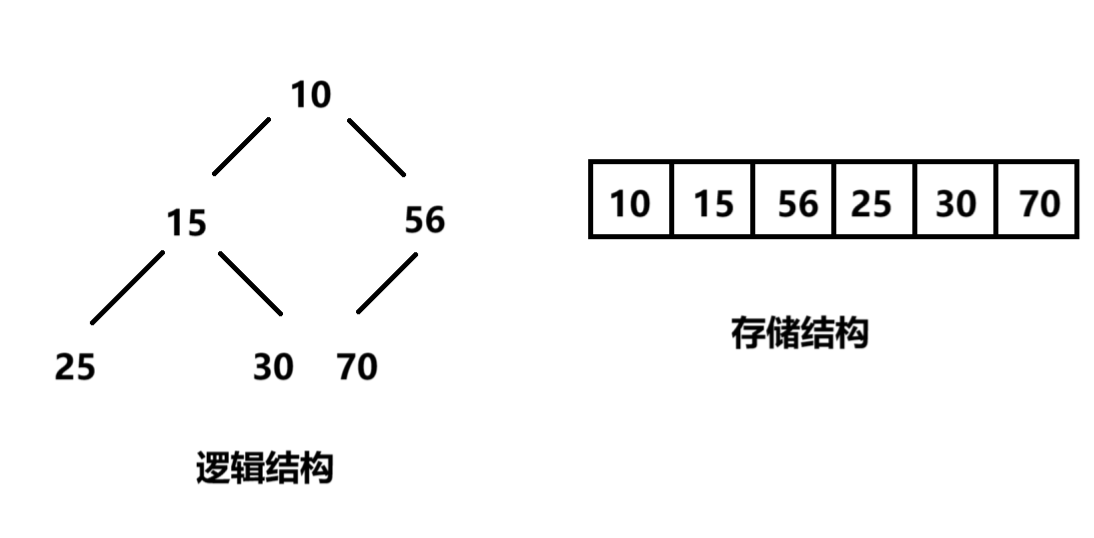
这里我们演示了一个小根堆的逻辑结构和存储结构

对于堆的实现来说，他有两个主要的调整算法，向上调整和向下调整算法

当构建堆时，我们采用向上调整算法，例如我们想建立一个小根堆，依次插入数据，当子节点小于父节点时，交换位置即可，直到不小于或者到达堆顶

当取出堆顶元素时，我们采用向下调整算法，同样是小根堆，我们将堆顶元素和最后一个元素调换位置，将最后一个元素弹出，再将此时的堆顶元素向下调整，当子节点小于父节点时交换位置

对于调整和插入的算法复杂度，由于这是二叉树的性质，我们可以直到最坏的情况也只需要将层数遍历一遍，时间复杂度为O(log n)

priority_queue 的介绍与使用

我们了解了堆的基本内容之后再回到优先队列，我们已经知道了他的本质就是一个堆，再来理解就会相当简单

这里我们可以看到，优先队列和队列于栈同样使用了容器适配器，但是默认是一个顺序表，这里也好理解，因为deque的随机访问性能极差，并且这里还出现了一个新的Compare模板是less，这里实际上是一个用于确定大根堆还是小根堆的接口，less表示大根堆，greater表示小根堆

函数	说明
priority_queue()/(first,last)	空构造与区间构造
empty()	判空
top()	返回堆顶元素
push()	插入
pop()	弹出堆顶元素

注意：

1. 默认优先队列是大堆

2. 想要变成小堆需要用到greater，示例如下

   #include<vector>
   #include<queue>
   #include<functional>int main()
   {vector<int> v{6,3,1,5,4,2};priority_queue<int,vector<int>,greater<int>> q2(v.begin(),v.end());return 0;
   }
   

3. 如果是自定义数据，就需要在自定义类型中提供比较运算符的重载才可以使用

要模拟实现优先级队列，我们需要介绍仿函数的内容，等到下一篇再介绍，感谢支持，如果你发现文章中有任何不严谨或者需要补充的部分，欢迎在评论区指出