图论 并查集 模拟 位运算—题841、127、684、685、657、31、463、1356 C++实现与有向图 无向图 并查集总结

文章目录

  • 841.钥匙和房间
    • DFS
    • BFS
  • 127. 单词接龙
  • 684.冗余连接
  • 685.冗余连接II
  • 657. 机器人能否返回原点
  • 31.下一个排列
  • 463. 岛屿的周长
    • 解法1
    • 解法2
  • 1356. 根据数字二进制下 1 的数目排序
    • 解法1
    • 解法2
  • 注意点

图论：题841、127
并查集：题684、685
模拟：题657、31、463
位运算：题1356

841.钥匙和房间

在这里插入图片描述
分析：

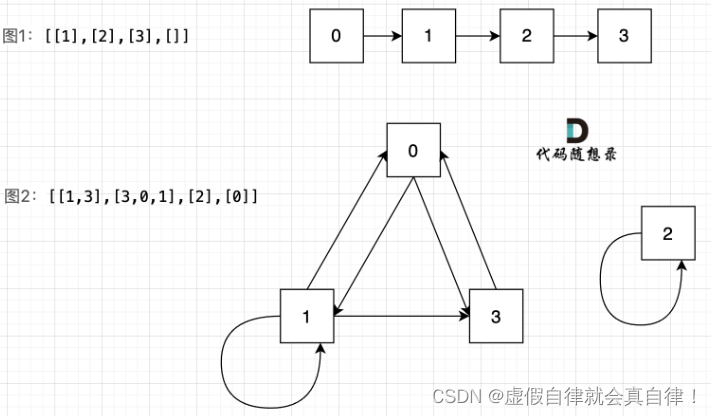
  1. 这道题是有向图，图1的所有节点都是连接的，而图二中的节点2 是孤立的，不能进入所有房间。孤立问题可以用并查集的方式去解决，但本题是有向图。
    图2中，0号房间拿到1、3号房间的钥匙，可以去1、3号房间；1号房间拿到0、1、3号房间的钥匙，可以去0、1、3号房间；2号房间只能拿到2号房间的钥匙；3号房间拿到0号房间的钥匙，可以去0号房间，只有2号房间是孤立的。

  2. 在有向图中，即使所有节点都是链接的，依然不能从0出发遍历所有边，如下，节点0只能去节点5。所以本题是一个有向图搜索全路径的问题。 只能用**深搜（DFS）或者广搜（BFS）**来搜索路径。

DFS

  1. 确认递归函数，参数
    需要传入二维数组rooms来遍历，当前的key，和记录走过的房间的布尔类型的一维数组visited。

  2. 确认终止条件
    在递归中，处理当前访问的节点，还是处理下一个要访问的节点？这决定终止条件怎么写。首先明确，本题中要处理的是visited数组，需要记录哪些房间是访问过的。visited数组默认元素都是false，如果遇到访问过的节点把元素标记为true。

  • 如果是处理当前访问的节点，当前节点在visited数组是 true ，说明访问过该节点，那就终止本层递归，否则在visited数组标记为true。
  • 如果是处理下一个要访问的节点，那么就不需要终止条件，而是在 搜索下一个节点的时候，直接判断 下一个节点是否是我们要搜的节点。
  1. 处理目前搜索节点出发的路径
    终止条件的两种写法决定了两种不一样的递归写法。通常有递归就有回溯，但是这道题是搜索所有路径，不需要回溯，只要遍历过的节点都标记，例如题797.所有可能的路径。当搜索一条可行路径的时候，就需要回溯操作了。没有回溯的话，就没法“调头”。

写法1，处理当前节点

class Solution {
public:bool canVisitAllRooms(vector<vector<int>>& rooms) {//写法1 处理当前节点vector<bool> visited(rooms.size(), false);dfs(rooms, visited, 0);//检查是否都访问到了for(int i : visited){if(i == false) return false;}return true;}
private://写法1 处理当前节点void dfs1(const vector<vector<int>>& rooms, vector<bool>& visited, int key){//如果访问过房间 终止本层递归if(visited[key]) return;//没有访问过，标记该房间为truevisited[key] = true;//获取当前房间的钥匙 进行下一轮的递归vector<int> keys = rooms[key];for(int key : keys) dfs1(rooms, visited, key);}
};

写法2，处理下一个节点

class Solution {
public:bool canVisitAllRooms(vector<vector<int>>& rooms) {vector<bool> visited(rooms.size(), false);//DFS写法2 处理下一个要访问节点visited[0] = true;//0号房间肯定被访问过dfs2(rooms, visited, 0);//检查是否都访问到了for(int i : visited){if(i == false) return false;}return true;}
private:void dfs2(const vector<vector<int>>& rooms, vector<bool>& visited, int key){//写法2是处理下一个节点 //遍历所有路径不需要终止条件 标记访问过的节点即可//获取当前房间的钥匙vector<int> keys = rooms[key];for(int key : keys){if(visited[key] == false){visited[key] = true;dfs2(rooms, visited, key);}}}
};

BFS

class Solution {
public:bool canVisitAllRooms(vector<vector<int>>& rooms) {//BFSreturn bfs(rooms);}
private:bool bfs(const vector<vector<int>>& rooms){vector<int> visited(rooms.size(), 0);visited[0] = 1;//0号房间开始 肯定被访问过queue<int> que;//模拟房间的遍历que.push(0);//0号房间开始while(!que.empty()){//访问当前房间int key = que.front(); que.pop();//获取当前房间的钥匙vector<int> keys = rooms[key];for(int key : keys){//如果该钥匙对应的房间没有被访问过if(!visited[key]){que.push(key);//该房间入队列visited[key] = 1;//标记房间}}}//检查是否都访问到了for(int i : visited){if(i == 0) return false;}return true;}
};

127. 单词接龙

在这里插入图片描述
分析

  1. 本题只需要求出最短路径的长度就可以了，不用找出路径——无向图求最短路径，广搜BFS最合适，从起点中心向四周扩散搜索，BFS找到终点就是最短路径
  2. 本题的关键在于，图中的线是如何连在一起的？起点和终点的最短路径长度？
  • 图中的线是如何连在一起的——如果单词只差一个字符就相连，需要判断
  • 起点和终点的最短路径长度——BFS，到达终点就是最短路径。使用深搜的话，还需要选择最短的路径。
  1. 本题是一个无向图，需要用标记位，标记着节点是否走过，否则就会死循环
  2. 本题给出集合是数组型的，可以转成set结构，查找更快一些
class Solution {
public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {// 将vector转成unordered_set，提高查询速度unordered_set<string> wordset(wordList.begin(), wordList.end());// 如果endWord没有在wordSet出现，直接返回0if(wordset.find(endWord) == wordset.end()) return 0;// 记录word是否访问过 <word, 起点到word路径的长度>unordered_map<string, int> visitmap;// 初始化队列queue<string> que;que.push(beginWord);//初始化visitmapvisitmap.insert(pair<string, int>(beginWord, 1));while(!que.empty()){string word = que.front(); que.pop();// 这个word的路径长度int pathlen = visitmap[word];for(int i=0; i<word.size(); i++){// 用一个新单词替换word，因为每次置换一个字母string newword = word;//hitfor(int j=0; j<26; j++){newword[i] = j + 'a';// 找到了end，返回path+1 cogif(newword == endWord) return pathlen + 1;// wordSet出现了newWord，并且newWord没有被访问过 hotif(wordset.find(newword) != wordset.end() && visitmap.find(newword) == visitmap.end()){// 添加访问信息visitmap.insert(pair<string, int>(newword, pathlen + 1));que.push(newword);}}}}return 0;}
};

684.冗余连接

在这里插入图片描述
并查集问题，集合问题

  1. 题目要求：1）删去的一条边使得结果图是一个有着N个节点的树，即只有一个根节点；2 ）如果有多个答案，则返回二维数组中最后出现的边。
  2. 从前向后遍历每一条边，优先让前面的边连上，边的两个节点如果不在同一个集合，就加入集合（即：同一个根节点）
  3. 如果节点a 和节点b 不在同一个集合，将两个 节点连在一起，加入集合，图1。如果边的两个节点已经出现在同一个集合里，说明着边的两个节点已经连在一起了，再加入这条边一定就出现环了，图2。

图1

图2

class Solution {
public:vector<int> findRedundantConnection(vector<vector<int>>& edges) {init();for(int i=0; i<edges.size(); i++){if(isSame(edges[i][0], edges[i][1])) return edges[i];else join(edges[i][0], edges[i][1]);}return {};}
private://构造并查集int n = 1005; //节点数量3 到1000//C++中的一种数据结构vector<int> father = vector<int> (n, 0);//并查集初始化void init(){for(int i=0; i<n; i++) father[i] = i;}//并查集里 寻找根节点//相当于判断节点是否出现在集合中int find(int root){return root == father[root] ? root : father[root] = find(father[root]);}//判断 两个节点是否找到同一个根//相当于判断两个节点是否出现在同一个集合bool isSame(int node1, int node2){node1 = find(node1);node2 = find(node2);return node1 == node2;}//两个节点连接 node2->node1void join(int node1, int node2){node1 = find(node1);node2 = find(node2);if(node1 == node2) return;father[node2] = node1;}
};

685.冗余连接II

  1. 题目的意思是题中的图原本是一棵树，只不过在不增加节点的情况下多加了一条边。还有如果存在多便可以删除的情况下，要删顺序靠后的边。

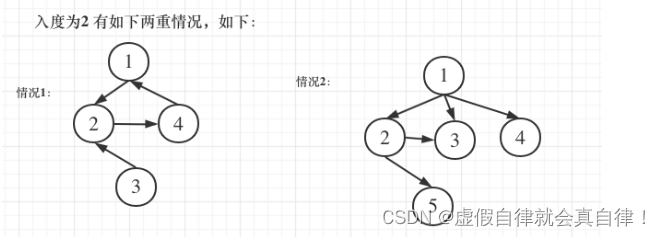
  2. 有三种情况，前两种是存在入度为2的节点，且只有一个节点入度为2，如图

  3. 情况1中，节点2来源于节点1和节点3，上层节点和下层节点。情况2中，节点3来源于节点1和节点2，父节点和同层节点。情况3中，没有入度为2的点，图中一定出现了有向环。因此，首先要计算节点的入度，也就是计算edges[i][1]。不考虑出度是因为出度没有意义，一个父节点有多个出度。

  4. 步骤

  • 计算节点的入度，也就是计算edges[i][1]。
  • 当节点入度为2时，要删除 指向该节点的两条边其中的一条。同时，要判断删除这个边，图是否为树，如果是。删除的边就是所求结果。
  • 还要注意从后向前遍历，要保证存在多边可以删除时，删除的是顺序靠后的边。
  • 当没有入度为2的情况时，存在有向环，构成环的边就是要删除的边。
  • 两个关键的函数，一个是判断删除边后图是否为树，另一个是存在有向环时，要找到需要删除的边。
  • 并查集，判断有向图能否构成树：在添加图之前，两个点所在的边 能够在并查集里找到相同的根，那么这条边加到图中得到的新图一定不是树。
class Solution {
public:vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {int inDegree[N] = {0};//记录节点入度n = edges.size();//边的数量//1.计算节点的入度for(int i=0; i<n; i++){inDegree[edges[i][1]]++;}vector<int> vec;//记录入度为2的边//2.找入度为2的节点所对应的边，要倒序，优先返回最后出现在二维数组中的答案for(int i=n-1; i>=0; i--){if(inDegree[edges[i][1]] == 2) vec.push_back(i);}//3.处理情况1和2 入度为2的节点//两条边中 要判断删除哪个边可以构成树if(vec.size() > 0){if(isTreeAfterRemoveEdge(edges, vec[0])) return edges[vec[0]];else return edges[vec[1]];}//4.处理情况3 没有入度为2的节点 有有向环return getRemoveEdge(edges);}
private:static const int N = 1010;//题目二维数组大小的在3到1000范围内int father[N];//并查集 数组int n;//边的数量//构造并查集的相关函数void init()//初始化{for(int i=1; i<=n; i++) father[i] = i;}//并查集寻根int find(int root){if(root == father[root]) return root;return father[root] = find(father[root]);//return root == father[root] ? root : father[root] = find(father[root]);}//将node2->node1 这条边加入并查集void join(int node1, int node2){node1 = find(node1);node2 = find(node2);if(node1 == node2) return;father[node2] = node1;}//判断是否同根bool isSame(int node1, int node2){node1 = find(node1);node2 = find(node2);return node1 == node2;}//有向图如果存在有向环，找到有向环中要删除的边，使其变成树vector<int> getRemoveEdge(const vector<vector<int>>& edges){init();//初始化并查集for(int i=0; i<n; i++){//找到有向环 两个节点同根->有向环if(isSame(edges[i][0], edges[i][1])) return edges[i];//不同根 则连接两节点join(edges[i][0], edges[i][1]);}return {};}//删一条边之后判断是不是树bool isTreeAfterRemoveEdge(vector<vector<int>>& edges, int deleteEdge){init();for(int i=0; i<n; i++){if(i == deleteEdge) continue;//有向环 一定不是树if(isSame(edges[i][0], edges[i][1])) return false;join(edges[i][0], edges[i][1]);}return true;}
};

657. 机器人能否返回原点

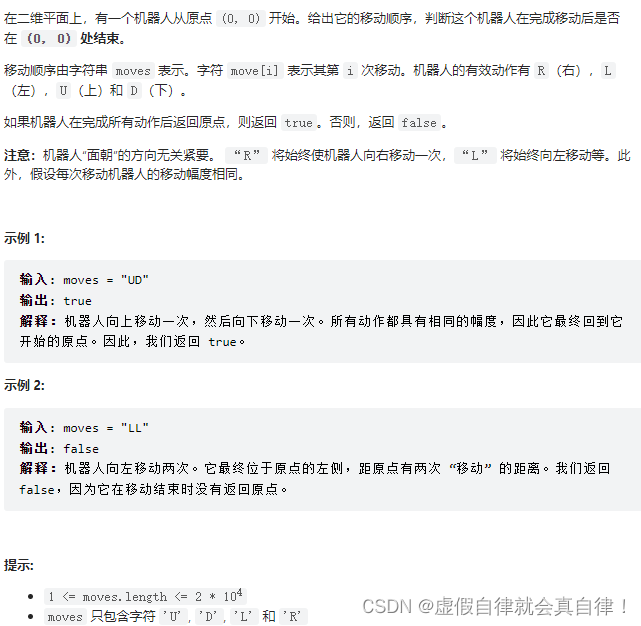
在这里插入图片描述
假设机器人位置(x，y)，初始为0，然后：
if (moves[i] == ‘U’) y++;
if (moves[i] == ‘D’) y–;
if (moves[i] == ‘L’) x–;
if (moves[i] == ‘R’) x++;
最后判断一下x，y是否回到了(0, 0)位置就可以了。

class Solution {
public:bool judgeCircle(string moves) {int x= 0 , y = 0;for(int i=0; i<moves.size(); i++){if(moves[i] == 'U') y++;if(moves[i] == 'D') y--;if(moves[i] == 'L') x++;if(moves[i] == 'R') x--;}if(x == 0 && y == 0) return true;return false;}
};

31.下一个排列

在这里插入图片描述

注意排列的有序性和从后面开始遍历。

class Solution {
public:void nextPermutation(vector<int>& nums) {for(int i=nums.size()-1; i>=0; i--){for(int j=nums.size()-1; j>i; j--){if(nums[j] > nums[i]){swap(nums[i], nums[j]);reverse(nums.begin() + i + 1, nums.end());return;}}}//此时整个数组是倒序的，反转一下便可reverse(nums.begin(), nums.end());}
};

463. 岛屿的周长

解法1

计算出总的岛屿数量，因为有一对相邻两个陆地，边的总数就减2，那么在计算出相邻岛屿的数量就可以了，如图：

写法1是直接计算边长，遇到一个岛屿，边长+4，遇到一个相邻岛屿，边长-2

class Solution {
public:int islandPerimeter(vector<vector<int>>& grid) {//解法1return round2(grid);}
private://解法1 写法1int round1(const vector<vector<int>>& grid){int result1 = 0;for(int i=0; i<grid.size(); i++)//遍历行{for(int j=0; j<grid[0].size(); j++)//遍历列{if(grid[i][j] == 1)//遇到岛屿{result1 += 4;//累加边长if(i > 0 && grid[i-1][j] == 1) result1 -= 2;if(j > 0 && grid[i][j-1] == 1) result1 -= 2;}}}return result1;}
};

写法2是统计岛屿数量与相邻岛屿数量，周长 = 岛屿数量4 - 相邻岛屿数量2（公共边）

class Solution {
public:int islandPerimeter(vector<vector<int>>& grid) {//解法1 周长 = 岛屿数量*4 - 相邻岛屿数量*2（公共边）return round2(grid);}
private://解法1 写法2int round2(const vector<vector<int>>& grid){int land = 0;int neiborland = 0;for(int i=0; i<grid.size(); i++)//遍历行{for(int j=0; j<grid[0].size(); j++)//遍历列{if(grid[i][j] == 1)//遇到岛屿{land++;//累加边长if(i > 0 && grid[i-1][j] == 1) neiborland++;if(j > 0 && grid[i][j-1] == 1) neiborland++;}}}return land*4 - neiborland*2;}
};

解法2

遍历每一个空格，遇到岛屿，看其上下左右四个方向是否为边界或者水域，如果遇到水域或者出界的情况，就可以计算边了，如图：

class Solution {
public:int islandPerimeter(vector<vector<int>>& grid) {//解法2 return round3(grid);}
private:int round3(const vector<vector<int>>& grid){//当前地图上下左右方向的情况int direction[4][2] = {0, 1, 1, 0, -1, 0, 0, -1};int result3 = 0;for(int i=0; i<grid.size(); i++){for(int j=0; j<grid[0].size(); j++){if(grid[i][j] == 1){for(int k=0; k<4; k++){int x = i + direction[k][0];int y = j + direction[k][1];if(x < 0|| x >= grid.size()|| y < 0|| y >= grid[0].size()|| grid[x][y] == 0) result3++;}}}}return result3;}
};

1356. 根据数字二进制下 1 的数目排序

考察如何计算一个数的二进制中1的数量

解法1

挨个计算1的数量，最多就是循环n的二进制位数，32位。

class Solution {
public:vector<int> sortByBits(vector<int>& arr) {sort(arr.begin(), arr.end(), compare);return arr;}
private:static bool compare(int a, int b){//解法1int bita = bitCount1(a);int bitb = bitCount1(b);//如果二进制1的数量相同，比较数值大小if(bita == bitb) return a < b;//升序return bita < bitb;}static int bitCount1(int n){int count = 0; // 计数器while (n > 0) {if((n & 1) == 1)  count++;  // 当前位是1，count++n >>= 1 ; // n向右移位}return count;}
};

解法2

只循环n的二进制中1的个数次，计算12的二进制1的数量为例，如图所示：

class Solution {
public:vector<int> sortByBits(vector<int>& arr) {sort(arr.begin(), arr.end(), compare);return arr;}
private:static bool compare(int a, int b){//解法2int bita = bitCount2(a);int bitb = bitCount2(b);//如果二进制1的数量相同，比较数值大小if(bita == bitb) return a < b;//升序return bita < bitb;}static int bitCount2(int n){int count = 0;while(n){n &= (n - 1);// 清除最低位的1count++;}return count;}
};

注意点

  1. 有向图，搜索全路径，深搜（DFS）或者广搜（BFS）；并查集可以判断有向图在加边之后图是否为树
  2. 无向图，求最短路径，广搜
  3. 并查集定义：并查集集是一种维护集合的数据结构，并查集支持两个操作
  • ① 合并：合并两个集合。在合并的过程中，只对两个不同的集合进行合并，如果两个元素在相同的集合中，那么就不会对它们进行操作。这就保证了在同一个集合中一定不会产生环，即并查集产生的每一个集合都是一棵树
  • ② 查找：判断两个元素是否在一个集合。
  1. 并查集是用数组实现的，int father[N];n，其中 father[i] 表示元素 i 的父亲结点，而父亲结点本身也是这个集合内的元素（1 ≤ i ≤ N）
  2. 并查集可以解决什么问题呢？
    主要解决集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。
  3. 并查集主要有三个功能。
  • 寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
  • 将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
  • 判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点
  1. 并查集举例说明

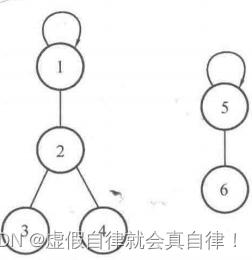
例如 father[1] = 2 就表示元素 1 的父亲结点是元素 2 ，以这种父系关系来表示元素所属的集合。另外，如果 father[i] = i ，则说明元素 i 是该集合的根结点，但对同一个集合来说只存在一个根结点，且将其作为所属集合的标识。

  1. 并查集判断有向图在加边前后能否构成树
    在添加图之前，两个点所在的边 能够在并查集里找到相同的根，那么这条边加到图中得到的新图一定不是树。

  2. 并查集模板如下，看题目情况修改模板中的 n

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构// 并查集初始化
void init() {for (int i = 0; i < n; ++i) {father[i] = i;}
}
// 并查集里寻根的过程
int find(int u) {return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {u = find(u);v = find(v);return u == v;
}// 将v->u 这条边加入并查集
void join(int u, int v) {u = find(u); // 寻找u的根v = find(v); // 寻找v的根if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回father[v] = u;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/29370.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

一百三十、海豚调度器——用DolphinScheduler定时调度HiveSQL任务

一百三十、海豚调度器——用DolphinScheduler定时调度HiveSQL任务

一、目标 用海豚调度器对Hive数仓各层数据库的SQL任务进行定时调度。比如&#xff0c;DWD层脱敏清洗表的动态插入数据、DWS层指标表的动态插入数据 二、工具版本 1、海豚调度器&#xff1a;apache-dolphinscheduler-2.0.5-bin.tar.gz 2、Hive&#xff1a;apache-hive-3.1.2…
阅读更多...
完整的电商平台后端API开发总结

完整的电商平台后端API开发总结

对于开发一个Web项目来说&#xff0c;无论是电商还是其他品类的项目&#xff0c;注册与登录模块都是必不可少的&#xff1b;注册登录功能也是我们在日常生活中最长接触的&#xff0c;对于这个业务场景的需求与逻辑大概是没有什么需要详细介绍的&#xff0c;市面上常见的邮箱注册…
阅读更多...
PyCharm 常用快捷键

PyCharm 常用快捷键

目录 1、代码编辑快捷键 2、搜索/替换快捷键 3、代码运行快捷键 4、代码调试快捷键 5、应用搜索快捷键 6、代码重构快捷键 7、动态模块快捷键 8、导航快捷键 9、通用快捷键 1、代码编辑快捷键 序号快捷键作用1CTRLALTSPACE快速导入任意类2CTRLSHIFTENTER代码补全3SHI…
阅读更多...
关于你欠缺的NoSQL中的redis和mongoDB

关于你欠缺的NoSQL中的redis和mongoDB

文章目录 前言一、在string list hash结构中&#xff0c;每个至少完成5个命令&#xff0c;包含插入 修改 删除 查询&#xff0c;list 和hash还需要增加遍历的操作命令1、STRING类型2、List类型数据的命令操作&#xff1a;3、举例说明list和hash的应用场景&#xff0c;每个至少一…
阅读更多...
数组的递归筛选

数组的递归筛选

数组递归筛选 根据一个值筛选出来通过 includes 递归 const options [{name: "ikun",options: [{name: "YAY11",},],},{name: "YAY",}, ];function findValue(orgOptions,val) {let newArr1 []orgOptions.forEach(item>{if(item.options…
阅读更多...
网络爬虫-网易易盾滑块验证码

网络爬虫-网易易盾滑块验证码

首先打开易盾官网&#xff0c;依次单击“在线体验”和“滑块拼图”选项&#xff0c;出现如下图所示的滑块验证码&#xff0c;滑动后发现Network面板成功抓包。 如图所示 其中主要的加密参数可以看出来就是acToken以及cb 我们接着下断点往下走 我通过上图可以看到 acToken&#…
阅读更多...
实例018 类似windows xp的程序界面

实例018 类似windows xp的程序界面

实例说明 在Windows XP环境下打开控制面板&#xff0c;会发现左侧的导航界面很实用。双击展开按钮&#xff0c;导航栏功能显示出来&#xff0c;双击收缩按钮&#xff0c;导航按钮收缩。下面通过实例介绍此种主窗体的设计方法。运行本例&#xff0c;效果如图1.18所示。 ​编辑…
阅读更多...
适合小公司的自动化部署脚本

适合小公司的自动化部署脚本

背景&#xff08;偷懒&#xff09; 在小小的公司里面&#xff0c;挖呀挖呀挖。快挖不动了&#xff0c;一件事重复个5次&#xff0c;还在人肉手工&#xff0c;身体和心理就开始不舒服了&#xff0c;并且违背了个人的座右铭&#xff1a;“偷懒”是人类进步的第一推动力。 每次想…
阅读更多...
ROS：nodelet

ROS：nodelet

目录 一、前言二、概念三、作用四、使用演示4.1案例简介4.2nodelet 基本使用语法4.3内置案例调用 五、nodelet实现5.1需求5.2流程5.3准备5.4创建插件类并注册插件5.5构建插件库5.6使插件可用于ROS工具链5.6.1配置xml5.6.2导出插件 5.7执行 一、前言 ROS通信是基于Node(节点)的…
阅读更多...
Rsync(二十七）

Rsync(二十七）

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 目录 前言 一、概述 二、特性 三、应用场景 四、数据的同步方式 五、rsync传输模式 六、rsync应用 七、rsync 命令 1. 格式 1.1 作为远程命令 1. 2 作为rsync服务 2. 选项 3.…
阅读更多...
分布式定时任务组件：XXL-JOB

分布式定时任务组件：XXL-JOB

一、GitHub源码地址 https://github.com/xuxueli/xxl-job 二、部署文档 参考&#xff1a;https://blog.csdn.net/qq798867485/article/details/131415408 三、初始化数据库SQL 1、xxl_job_user XxlJob-用户管理 2、xxl_job_group XxlJob-执行器管理 3、xxl…
阅读更多...
〖码银送书第三期〗《Python机器学习：基于PyTorch和Scikit-Learn》

〖码银送书第三期〗《Python机器学习：基于PyTorch和Scikit-Learn》

前言 近年来&#xff0c;机器学习方法凭借其理解海量数据和自主决策的能力&#xff0c;已在医疗保健、 机器人、生物学、物理学、大众消费和互联网服务等行业得到了广泛的应用。自从AlexNet模型在2012年ImageNet大赛被提出以来&#xff0c;机器学习和深度学习迅猛发展&#xf…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023