自底向上分析的分类如下所示:
![]()
算符优先分析
算符优先分析只规定算符之间的优先关系,也就是只考虑终结符之间的优先关系。
(一)若有文法G,如果G没有形如A->..BC..的产生式,其中B和C为非终结符,则称G为算符文法。
以下例子中G就是算符文法(没有连在一起的非终结符)
E->T|E+T|E-T
T->F|T*F|T/F
F->(E)|i
(二)

这里就用=,< 和 > 代替:
(1)a=b,当且仅当G中含有形如A--->..ab...或A---->...aBb...的产生式
(2)a<b,当且仅当G种含有形如A--->...aB...的产生式,且B能多步推导出右侧式子
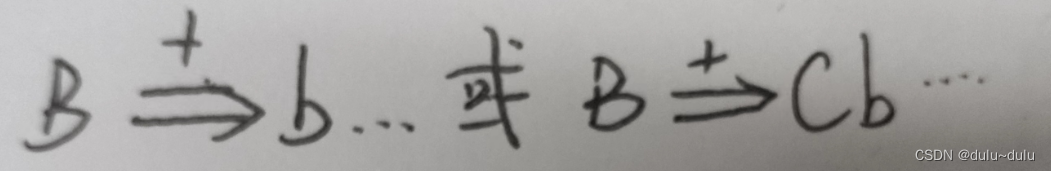
(3)a>b,当且仅当G中含有形如A--->...Bb...的产生式,且B能多步推导出右侧式子

这里理解起来也很简单,a<b,那么a就要小于B推导出的式子中最前面的终结符b,a>b同理
这里的推导较为复杂,我们可以演化出下面这一方法:

这样a<b,a>b的定义就为:
a<b,当且仅当G种含有形如A--->...aB...的产生式,且a小于B的FIRSTVT集合中的所有终结符
a>b,当且仅当G中含有形如A--->...Bb...的产生式,且B的LASTVT的所有终结符大于b
构造规则:
FIRSTVT:
(1)若有T->a...或T->Ra...,则aFIRSTVT(T)
(2)若有aFIRSTVT(R),且有产生式T->R...,则a
FIRSTVT(T)
LASTVT:
(1)若有T->...a或T->...aR,则aLASTVT(T)
(2)若aLASTVT(R),且产生式T->...R,则a
LASTVT
(三)设有一个不含产生式的算符文法G,如果任一终结符对(a,b)之间至多只有<,>,=3种关系种的一种成立,则称G是一个算符优先文法。即,两个终结符之间的优先关系是有序的,允许有a>b,b<a同时存在,但是不允许有a<b,a>b,a=b3种关系中的任一两种关系同时存在。
示例: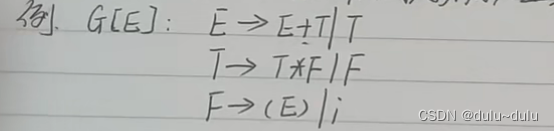
FIRSTVT集合:
(1)首先根据E->E+T|T的E->E+T,可得(注:行代表终结符,列代表非终结符)

(2)再看E->E+T|T 的E->T,需要把T的FIRSTVT元素放到E中,但是此时T中没有✔元素,所以

(3)T->T*F|F中的T->T*F

(4)T->T*F|F中的T->F,而F没有✔项

(5)F->(E)|i 中的F->(E)
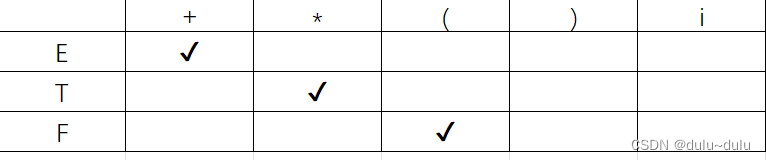
(6)F->(E)|i 中的F->i
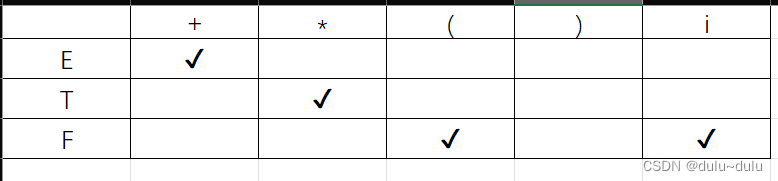
这是第一遍遍历式子,因为表有变化,所以要继续进行遍历,直到表不变
(1)首先根据E->E+T|T的E->E+T,可得

(2)再看E->E+T|T 的E->T,需要把T的FIRSTVT元素放到E中

(3)T->T*F|F中的T->T*F

(4)T->T*F|F中的T->F,将F中的✔项放到T中

表依旧有改变,继续遍历,直到没有出现新的内容
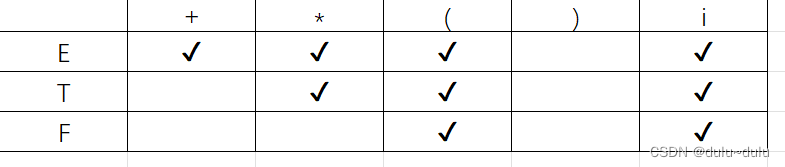
所以得出结论:
E(FIRSTVT)={+,*,{,},i}
T(FIRSTVT)={*,(,i}
F(FIRSTVT)={(,i}
LASTVT的操作步骤同理,得到:

接下来继续回到算符优先关系中
竖列表示在前面的终结符,横列表示在后面的终结符
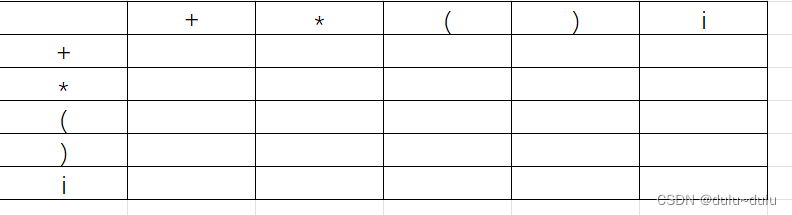
针对a=b
F->(E)|i,这里的“(”和“)”遵循a=b的定义,即A->..aBb...
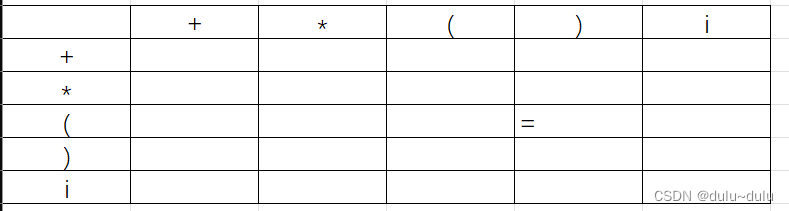
针对a<b,就是要找到a后面跟的非终结符,这个非终结符中的FIRSTVT集合的元素就是满足要求的元素。
E->E+T|T中的+T,T(FIRSTVT)= {*,(,i}
T->T*F|F中的*F,F(FIRSYVT) = {(,i}
F->(E)|i中的(E,E(FIRSTVT)= {+,*,{,},i}
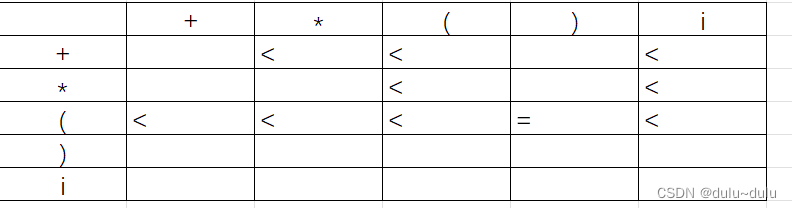
针对a>b,就是要找到a前面跟的非终结符,这个非终结符中的LASTVT集合的元素就是满足要求的元素:
E->E+T|T中的E+
T->T*F|F的T*
F->(E)|i 的E)
最终得到:
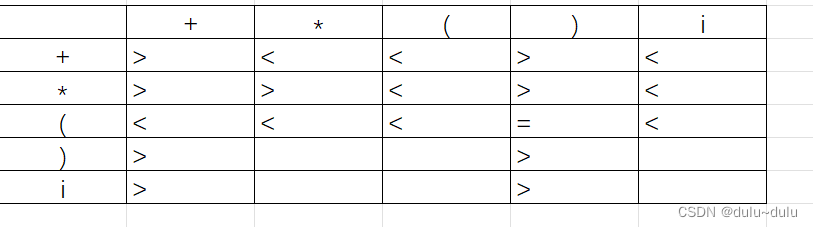
总结:
对于a<b,就要找终结符后面的非终结符(*F)的FIRSTVT集合(F的FIRSTVT集合)
对于a>b,就要找终结符前面的非终结符(F*)的LASTVT集合(F的LASTVT集合)