2016年第五届数学建模国际赛小美赛
B题 直达地铁线路
原题再现:
在目前的大都市地铁网络中,在两个相距遥远的车站之间运送乘客通常需要很长时间。我们可以建议在两个长途车站之间设置直达班车,以节省长途乘客的时间。
第一部分:请制定一个数学框架来优化终点站的选择,并评估建议的预期结果。
第二部分。如果你调整列车间隔或修建直达专线,探索你在经济和社会效益方面可能取得的任何优势。
第三部分给你所在城市的市长写一封两页的信,总结你的分析。把你的火车时刻表写在信的第二页。
整体求解过程概述(摘要)
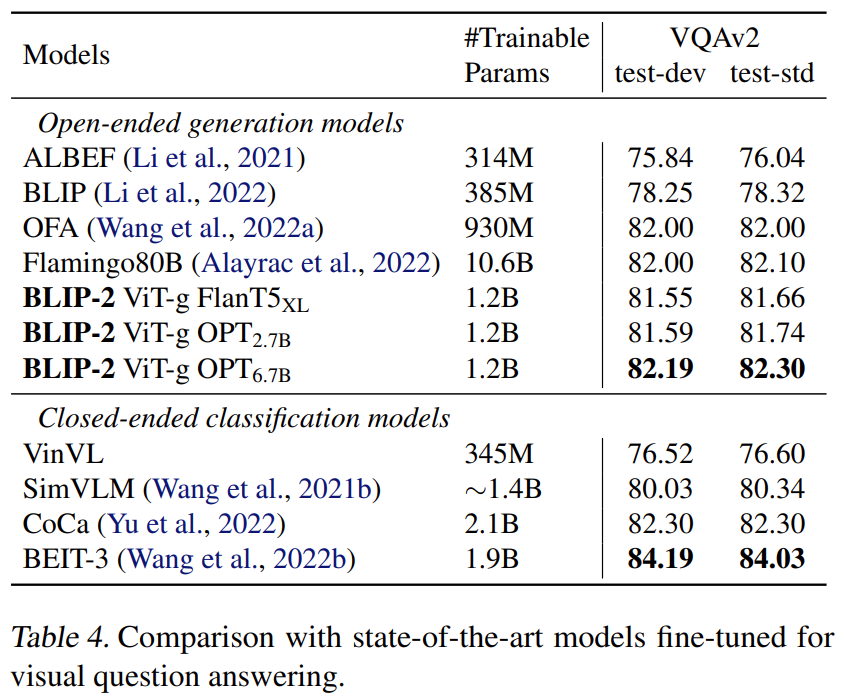
本文对影响地铁两站间直达站设置的各个因素进行了模型研究。然后,我们可以确定是否建立一个直接的地铁站之间的两个遥远的车站。如果有必要,我们会对其进行优化。接下来,以北京为例。通过确定路线,给出了在社会经济等多种因素影响下的最佳发车时间。
模型一。首先,采用控制变量法,分析了地铁乘客的个人情况、时间和周围环境对客流的影响。然后利用logit模型对拟合结果进行验证。得出结论:处于工人阶级中间的年轻人经常出现的地区,如工业区、行政区、交通枢纽等,客流最大。通过对北京地铁线路距离的获取,利用数据平均法研究了距离对位置的影响,得出当两站点间直线距离大于15km时,应考虑建立直达地铁。
模型二。基于模型1的结论,采用Floyd算法计算客流和两地距离对地铁位置的影响。发现它们之间的关系成为正态分布和最高点两个站点,其中需要建立地铁直达的站点最好。并以北京市为例,利用该结论得出了首都国际机场3号航站楼地铁站到回龙观地铁站的直达线路。
模型三。通过遗传分析,利用MATLAB对模型二确定的北京线位置进行优化。最后,我们知道当地铁站位于隆泽和回龙观之间时,这个站点是最好的选择。
模型四。通过查阅相关文献,分析了首都国际机场3号航站楼地铁站至回龙观地铁站直达线路的社会效益、经济效益和旅客时间效益。将主成分分析与实证分析相结合,得出不同时段地铁发车间隔时间不同的结论。地铁的运行时间是6:00-23:45。在6:00-10:00和16:00-20:00,每10分钟一班,其余时间15分钟一班。
综上所述,当两站点之间的直线距离大于15km时,尤其是交通枢纽、工业区和行政区,且高峰时段最需要短间隔时间时,应考虑建立直达地铁。
模型假设:
1、不考虑地铁停车系统的需要。
2、假设两个长途车站之间的直达地铁对其他地铁系统没有影响。
3、假设地铁网络的一致性对地铁模型没有影响。
4、假定场地交通功能对本文构建的地铁模型无影响。
5、假设项目成本、效益、技术可行性等因素对第一部分模型无影响6、假设地铁始终准时,不会因外部因素造成延误。
问题重述:
为什么需要在两个相距较远的车站之间更换线路
在目前大城市的地铁网络中,在两个相距较远的车站之间运送乘客通常需要很长的时间。我们可以建议在两个长途车站之间设置直达班车,以节省长途旅客的时间。
我们需要解决的问题
1。如何建立一个数学框架来优化终端站的选择?如何评价最佳建议的预期效果?
2、如何调整列车间隔或建设直达专用线,发挥其经济效益和社会效益?
3、偿付能力如何处理?
写一封两页的信给市长,总结我们的分析,简要描述我们的设计特点和优势。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
function m_main()
clear
clc
Max_gen = 100;
pop_size = 100;
chromsome = 10;
pc = 0.9;
pm = 0.25;
gen = 0;
init = 40*rand(pop_size, chromsome)-20;
pop = init;
fit = obj_fitness(pop);
[max_fit, index_max] = max(fit);
maxfit = max_fit;
[min_fit, index_min] = min(fit);
best_indiv = pop(index_max, :);
while gen<Max_gen
gen = gen+1;
bt(gen) = max_fit;
if maxfit<max_fit;
maxfit = max_fit;
pop(index_min, :) = pop(index_max, :);
best_indiv = pop(index_max, :);
end
best_indiv_tmp(gen) = pop(index_max);
newpop = ga(pop, pc, pm, chromsome, fit);
fit = obj_fitness(newpop);
[max_fit, index_max] = max(fit);
[min_fit, index_min] = min(fit);
pop = newpop;
trace(1, gen) = max_fit;
trace(2, gen) = sum(fit)./length(fit);
end
[f_max gen_ct] = max(bt)
maxfit
best_indiv
hold on
plot(trace(1, :), '.g:');
plot( trace(2, :), '.r-');
title('The experimental results in figure')
xlabel('The number of iterations/generation'), ylabel('The optimal structural');plot(gen_ct-1, 0:0.1:f_max+1, 'c-');
text(gen_ct, f_max+1, 'The maximum')
hold off
function [fitness] = obj_fitness(pop)
[r c] = size(pop);
x = pop;
fitness = zeros(r, 1);
for i = 1:r
for j = 1:c
fitness(i,1) = fitness(i, 1)+sin(sqrt(abs(40*x(i))))+1-abs(x(i))/20.0;
end
end
end
function newpop = ga(pop, pc, pm, chromsome, fit)
pop_size = size(pop, 1);
ps = fit/sum(fit);
pscum = cumsum(ps);%size(pscum)
r = rand(1, pop_size);
qw = pscum*ones(1, pop_size);
selected = sum(pscum*ones(1, pop_size)<ones(pop_size, 1)*r)+1;
newpop = pop(selected, :);
if pop_size/2 ~= 0
pop_size = pop_size-1;
end
for i = 1:2:pop_size-1
while pc>rand
c_pt = round(8*rand+1);
pop_tp1 = newpop(i, :);pop_tp2 = newpop(i+1, :);
newpop(i+1, 1:c_pt) = pop_tp1(1, 1:c_pt);
newpop(i, c_pt+1:chromsome) = pop_tp2(1, c_pt+1:chromsome);
end
end
for i = 1:pop_size
if pm>rand
m_pt = 1+round(9*rand);
newpop(i, m_pt) = 40*rand-20;
end
end
end
end
f_max =
19.7139
gen_ct =
32
maxfit =
19.7139
best_indiv =
0.0804 -9.8254 -1.1084 19.7403 -8.1866 -13.6728 -17.6449 3.7018
-15.0008 8.797
function Z=drawGaussian(u,v,x,y)
% u,vector,expactation;v,covariance matrix
%x=150:0.5:190;
%y=35:110;
[X,Y]=meshgrid(x,y);
DX=v(1,1);
dx=sqrt(DX);
DY=v(2,2);
dy=sqrt(DY);
COV=v(1,2);
r=COV/(dx*dy);
part1=1/(2*pi*dx*dy*sqrt(1-r^2));
p1=-1/(2*(1-r^2));
px=(X-u(1)).^2./DX;
py=(Y-u(2)).^2./DY;
pxy=2*r.*(X-u(1)).*(Y-u(2))./(dx*dy);
Z=part1*exp(p1*(px-pxy+py));
mesh(x,y,Z);