基本概念:
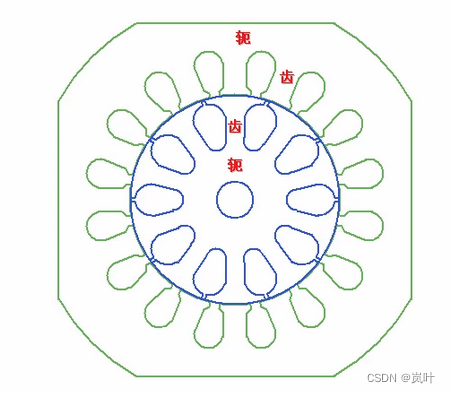
定子或者转子上有铁心或者绕铜线的地方,绕铜线的地方叫槽,而将槽分开的叫齿,将所有的齿连起来的部位较轭部。
磁感应强度与磁场强度之间的关系可以通过以下公式表示:
B=μH
其中,B 是磁感应强度,H 是磁场强度,μ 是磁导率。这个关系表明,在给定磁场强度下,磁感应强度与磁导率成正比。
与磁导计算相关的公式涉及到磁场、磁感应强度、磁势等概念。以下是一些与磁导计算相关的基本公式:
1. **磁感应强度和磁导的关系:**
\[ \mathbf{B} = \Lambda \mathbf{H} \]
其中,\(\mathbf{B}\) 是磁感应强度,\(\Lambda\) 是磁导,\(\mathbf{H}\) 是磁场强度。
2. **电磁感应定律:**
\[ \varepsilon = -\frac{d\Phi}{dt} \]
这里,\(\varepsilon\) 是感应电动势,\(\Phi\) 是磁通量。磁通量与磁导的关系为 \(\Phi = \Lambda \cdot \mathbf{H} \cdot A\),其中 \(A\) 是截面积。
3. **磁场中的高斯定律:**
\[ \nabla \cdot \mathbf{B} = 0 \]
在没有自由磁荷的情况下,磁场中的高斯定律表明磁感应强度的散度为零。
4. **磁场中的安培环路定理:**
\[ \oint \mathbf{H} \cdot d\mathbf{l} = I_{\text{enclosed}} \]
这个定理表示磁场中的环路积分等于被该环路所包围的电流的代数和。在这个公式中,\(\mathbf{H}\) 是磁场强度,\(I_{\text{enclosed}}\) 是被环路包围的电流。
5. **磁场中的能量密度:**
\[ u = \frac{1}{2} \Lambda \mathbf{H}^2 \]
其中,\(u\) 是单位体积内的磁场能量密度。
这些公式提供了磁导与磁场、电动势、电流等物理量之间的关系,是在电磁学和电机工程中进行磁场分析和计算时的基础。具体的应用还需要根据具体情境选择适当的公式。
---------------------------------------
电生磁
- F = N·I,N表示线圈匝数,I表示线圈中的电流大小。通电线圈产生的磁动势 F 等于线圈的匝数 N 和线圈中所通过的电流 I 的乘积,也叫磁通势,磁动势F的单位是安培(A)。
- F=Φ·Rm,Φ=B*S(S为与磁场方向垂直的平面的面积),Rm=L/μA(L表示磁路长度,A表示磁路横截面积)。作用在磁路上的磁动势 F 等于磁路内的磁通量 Φ 与磁阻Rm的乘积。
- F = H·L,(H为磁场强度,与磁密度B和磁路材料等有关) L表示磁路长度。F是磁场强度H在磁路L上的积分。
磁生电
- 电磁感应现象:当穿过闭合导体回路的磁通量发生变化时,不管这种变化是由什么原因引起的,闭合导体回路中就会出现电流,称之为电磁感应现象。
- 感应电动势的公式:<