凸优化 2:如何判定凸函数?
- 如何判断一个目标函数是凸函数?
- 如果是凸函数,那ta的定义域是凸集合
- 一个函数求俩次梯度,大于等于0,那这个函数就是一个凸函数
- 在同样条件下,怎么设计为凸函数模型?
- 怎么求解非凸函数?
- 怎么对非凸函数松弛,变成凸函数?
如何判断一个目标函数是凸函数?
为了判断一个函数是否是凸的,可以进行以下检查:
-
检查直线条件:试着在函数的图像上随便选两点,然后画一条直线连接这两点。如果这条直线总是位于这两点之间的函数图像之上或正好是这段曲线,那么这个函数就是凸函数。适用于:低维(通常是一维或二维)问题
-
检查斜率:如果你会计算斜率,你可以看斜率是否随着从左往右移动而不减少。这意味着当你朝着一个方向走过山的时候,坡度要么保持不变,要么变得更陡(非递减的),但绝不会突然变缓。适用于:一维问题。
-
使用二次导数:如果一个函数的二次导数总是大于或等于零,那么这个函数就是凸函数。这是因为二次导数告诉我们函数曲线弯曲的程度,如果它总是正的,说明函数曲线始终向上凸起。适用于:具有明确二次导数的函数。
如果是凸函数,那ta的定义域是凸集合
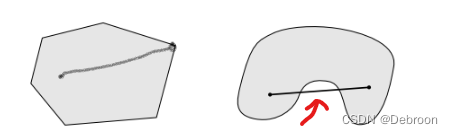
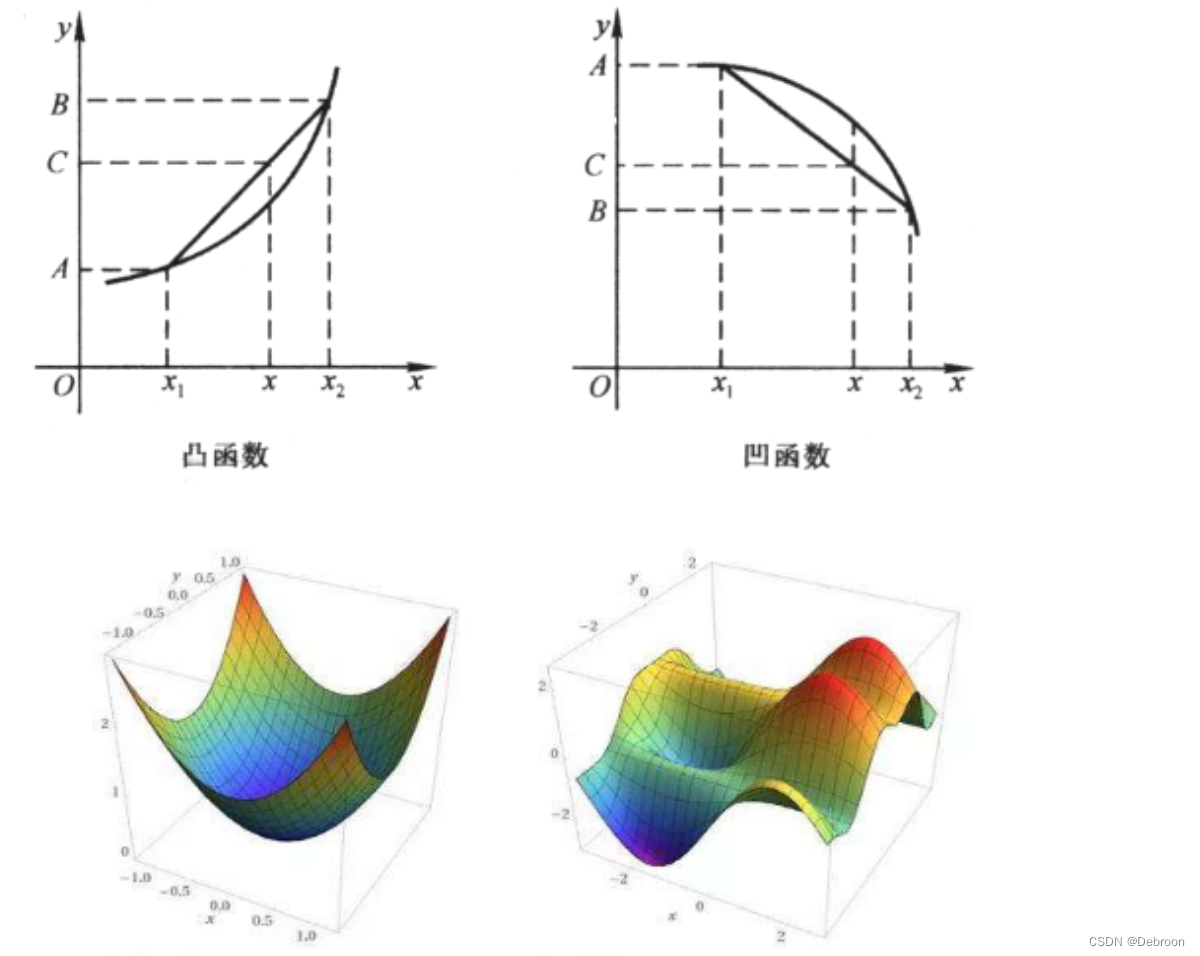
左图,凸集合就像一个没有凹陷的形状,内部包含了所有连接边上任意两点的线段。
右图,非凸集合就像一个有凹陷的形状,我能找到内部的俩个点,使得他们之间的直线超出内部范围。
这个函数的一个重要性质是,任意两点之间的连线都在函数图像的内部或者重合(加粗)。
-
这确保在其定义域内的任意局部最优解,同时也是全局最优解。
-
即任何局部最小值,都是全局最小值。
再把上面加粗的话,转换成数学语言::
- 凸函数的定义域是凸集,对于定义域任意 x、y,函数满足: f ( θ x + ( 1 − θ ) y ) ≤ θ f ( x ) + ( 1 − θ ) f ( y ) θ ∈ ( 0 , 1 ) f(\theta x+(1-\theta)y)\leq\theta f(x)+(1-\theta)f(y)\quad\theta\in(0,1) f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)θ∈(0,1)
这就是凸函数定义1。
一个函数求俩次梯度,大于等于0,那这个函数就是一个凸函数
如果一个函数求俩次梯度,依然大于等于0,那这个函数就是一个凸函数。
意味着它的图形永远是向上凸的,就像一个山丘。
如果一个山丘(函数)在任何地方,都至少是平的(等于0)或者向上弯曲的(>0),不会让你掉下去。
转换为数学语言:
- 凸函数定义2: ∇ 2 f ( x ) ⪰ 0 \nabla^{2}f(x)\succeq0 ∇2f(x)⪰0
- 对于凹函数: ∇ 2 f ( x ) ⪯ 0 \nabla^{2}f(x)\preceq0 ∇2f(x)⪯0