树与图的深度优先遍历、宽度优先遍历算法总结-编程知识

树与图的深度优先遍历、宽度优先遍历算法总结

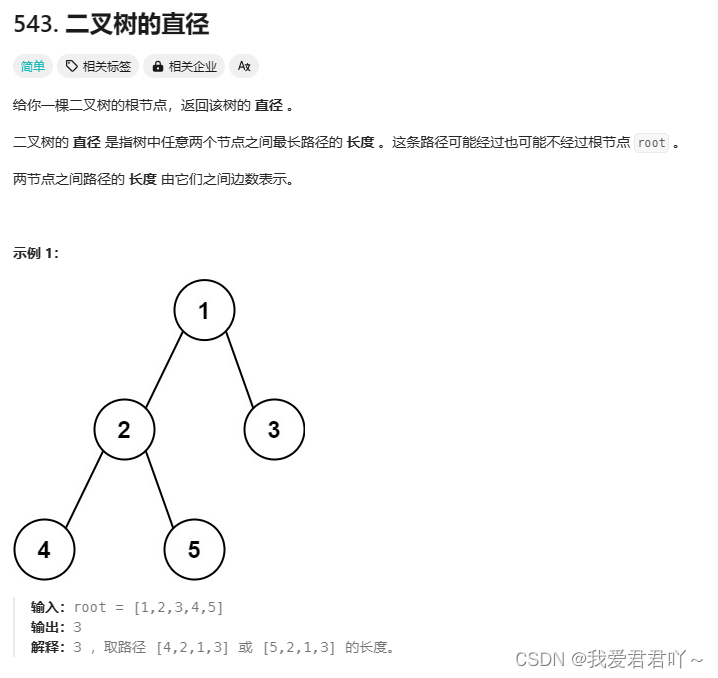
知识概览

树是特殊的图，是无环连通图
图分为有向图和无向图。因为无向图可以转化为有向图，树可以转化为图。因此本文讨论有向图。

树和图的存储：

邻接矩阵：空间复杂度 $O(n^2)$ ，适合存储稠密图。
邻接表：存储每个点可以到达哪些点，适合存储稀疏图。

树和图的遍历

树和图的深度优先遍历

例题展示

题目链接

活动 - AcWing系统讲解常用算法与数据结构，给出相应代码模板，并会布置、讲解相应的基础算法题目。https://www.acwing.com/problem/content/848/

代码

#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010, M = N * 2;int n;
int h[N], e[M], ne[M], idx;
bool st[N];int ans = N;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}// 以u为根的子树中点的数量
int dfs(int u)
{st[u] = true;  // 标记一下，已经被搜过了int sum = 1, res = 0;for (int i = h[u]; i != -1; i = ne[i]){int j = e[i];if (!st[j]){int s = dfs(j);res = max(res, s);sum += s;}}res = max(res, n - sum);ans = min(ans, res);return sum;
}int main()
{cin >> n;memset(h, -1, sizeof h);for (int i = 0; i < n - 1; i++){int a, b;cin >> a >> b;add(a, b), add(b, a);}dfs(1);cout << ans << endl;return 0;
}

树和图的宽度优先遍历

例题展示

题目链接

活动 - AcWing系统讲解常用算法与数据结构，给出相应代码模板，并会布置、讲解相应的基础算法题目。https://www.acwing.com/problem/content/849/

代码

#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 100010;int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int bfs()
{int hh = 0, tt = 0;q[0] = 1;memset(d, -1, sizeof d);d[1] = 0;while (hh <= tt){int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]){int j = e[i];if (d[j] == -1){d[j] = d[t] + 1;q[++tt] = j;}}}return d[n];
}int main()
{cin >> n >> m;memset(h, -1, sizeof h);for (int i = 0; i < m; i++){int a, b;cin >> a >> b;add(a, b);}cout << bfs() << endl;return 0;
}