【23-24 秋学期】NNDL 作业12 优化算法2D可视化-编程知识

1.简要介绍图中的优化算法，编程实现并2D可视化

SGD：随机梯度下降，每次迭代采集1个样本（随机）。

AdaGrad算法：一种梯度下降法，是对批量梯度下降法的改进，但并不是对动量法的改进。它的目的是在解决优化问题时自动调整学习率，以便能够更快地收敛。

RMSprop算法：与AdaGrad算法的区别在于 𝑮𝑮 𝒕𝒕 的计算由累积方式变成了指数衰减移动平均。

Momentum算法：用之前积累动量替代真正的梯度，在第𝑡𝑡次迭代时，计算负梯度的 指数加权移动平均作为参数的更新方向。

Adam: 自适应矩估计（ ada ptive m oment estimation），Adam 算法 ≈ 动量法 + RMSprop

参考老师ppt和 6.7 AdaGrad算法「梗直哥深度学习公开课」 - 知乎 (zhihu.com)

【收藏版】深度学习中的各种优化算法 (360doc.com)

（1）被优化函数 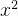$x^{2}$

SGD：

from nndl.op import Op
import torch
import numpy as np
from matplotlib import pyplot as pltfrom nndl.opitimizer import SimpleBatchGD# 被优化函数
class OptimizedFunction(Op):def __init__(self, w):super(OptimizedFunction, self).__init__()self.w = wself.params = {'x': 0}self.grads = {'x': 0}def forward(self, x):self.params['x'] = xreturn torch.matmul(self.w.T, torch.tensor(torch.square(self.params['x']), dtype=torch.float32))def backward(self):self.grads['x'] = 2 * torch.multiply(self.w.T, self.params['x'])# SGD梯度更新
import copydef train_f(model, optimizer, x_init, epoch):x = x_initall_x = []losses = []for i in range(epoch):all_x.append(copy.copy(x.numpy()))loss = model(x)losses.append(loss)model.backward()optimizer.step()x = model.params['x']print(all_x)return torch.tensor(all_x), losses# 可视化
class Visualization(object):def __init__(self):"""初始化可视化类"""# 只画出参数x1和x2在区间[-5, 5]的曲线部分x1 = np.arange(-5, 5, 0.1)x2 = np.arange(-5, 5, 0.1)x1, x2 = np.meshgrid(x1, x2)self.init_x = torch.tensor([x1, x2])def plot_2d(self, model, x, fig_name):"""可视化参数更新轨迹"""fig, ax = plt.subplots(figsize=(10, 6))cp = ax.contourf(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)),colors=['#e4007f', '#f19ec2', '#e86096', '#eb7aaa', '#f6c8dc', '#f5f5f5', '#000000'])c = ax.contour(self.init_x[0], self.init_x[1], model(self.init_x.transpose(0, 1)), colors='black')cbar = fig.colorbar(cp)ax.plot(x[:, 0], x[:, 1], '-o', color='#000000')ax.plot(0, 'r*', markersize=18, color='#fefefe')ax.set_xlabel('$x1$')ax.set_ylabel('$x2$')ax.set_xlim((-2, 5))ax.set_ylim((-2, 5))plt.savefig(fig_name)plt.show()def train_and_plot_f(model, optimizer, epoch, fig_name):"""训练模型并可视化参数更新轨迹"""# 设置x的初始值x_init = torch.tensor([3, 4], dtype=torch.float32)print('x1 initiate: {}, x2 initiate: {}'.format(x_init[0].numpy(), x_init[1].numpy()))x, losses = train_f(model, optimizer, x_init, epoch)print(x)losses = np.array(losses)# 展示x1、x2的更新轨迹vis = Visualization()vis.plot_2d(model, x, fig_name)# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = SimpleBatchGD(init_lr=0.2, model=model)
train_and_plot_f(model, opt, epoch=20, fig_name='opti-vis-para.pdf')

结果如下：

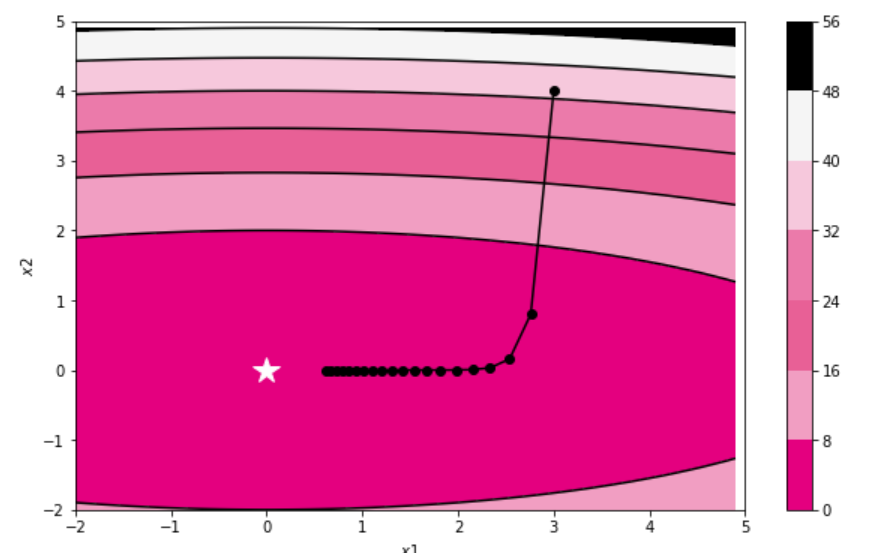
AdaGrad:

from nndl.opitimizer import Optimizer
class Adagrad(Optimizer):def __init__(self, init_lr, model, epsilon):"""Adagrad 优化器初始化输入：- init_lr： 初始学习率- model：模型，model.params存储模型参数值- epsilon：保持数值稳定性而设置的非常小的常数"""super(Adagrad, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.epsilon = epsilondef adagrad(self, x, gradient_x, G, init_lr):"""adagrad算法更新参数，G为参数梯度平方的累计值。"""G += gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.adagrad(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Adagrad(init_lr=0.5, model=model, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para2.pdf')
plt.show()

结果如下：

RMSprop：

 
class RMSprop(Optimizer):def __init__(self, init_lr, model, beta, epsilon):"""RMSprop优化器初始化输入：- init_lr：初始学习率- model：模型，model.params存储模型参数值- beta：衰减率- epsilon：保持数值稳定性而设置的常数"""super(RMSprop, self).__init__(init_lr=init_lr, model=model)self.G = {}for key in self.model.params.keys():self.G[key] = 0self.beta = betaself.epsilon = epsilondef rmsprop(self, x, gradient_x, G, init_lr):"""rmsprop算法更新参数，G为迭代梯度平方的加权移动平均"""G = self.beta * G + (1 - self.beta) * gradient_x ** 2x -= init_lr / torch.sqrt(G + self.epsilon) * gradient_xreturn x, Gdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.G[key] = self.rmsprop(self.model.params[key],self.model.grads[key],self.G[key],self.init_lr)# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = RMSprop(init_lr=0.1, model=model, beta=0.9, epsilon=1e-7)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para3.pdf')

结果如下：

Momentum（动量法） ：

class Momentum(Optimizer):def __init__(self, init_lr, model, rho):"""Momentum优化器初始化输入：- init_lr：初始学习率- model：模型，model.params存储模型参数值- rho：动量因子"""super(Momentum, self).__init__(init_lr=init_lr, model=model)self.delta_x = {}for key in self.model.params.keys():self.delta_x[key] = 0self.rho = rhodef momentum(self, x, gradient_x, delta_x, init_lr):"""momentum算法更新参数，delta_x为梯度的加权移动平均"""delta_x = self.rho * delta_x - init_lr * gradient_xx += delta_xreturn x, delta_xdef step(self):"""参数更新"""for key in self.model.params.keys():self.model.params[key], self.delta_x[key] = self.momentum(self.model.params[key],self.model.grads[key],self.delta_x[key],self.init_lr)# 固定随机种子
torch.manual_seed(0)
w = torch.tensor([0.2, 2])
model = OptimizedFunction(w)
opt = Momentum(init_lr=0.01, model=model, rho=0.9)
train_and_plot_f(model, opt, epoch=50, fig_name='opti-vis-para4.pdf')

结果如下：

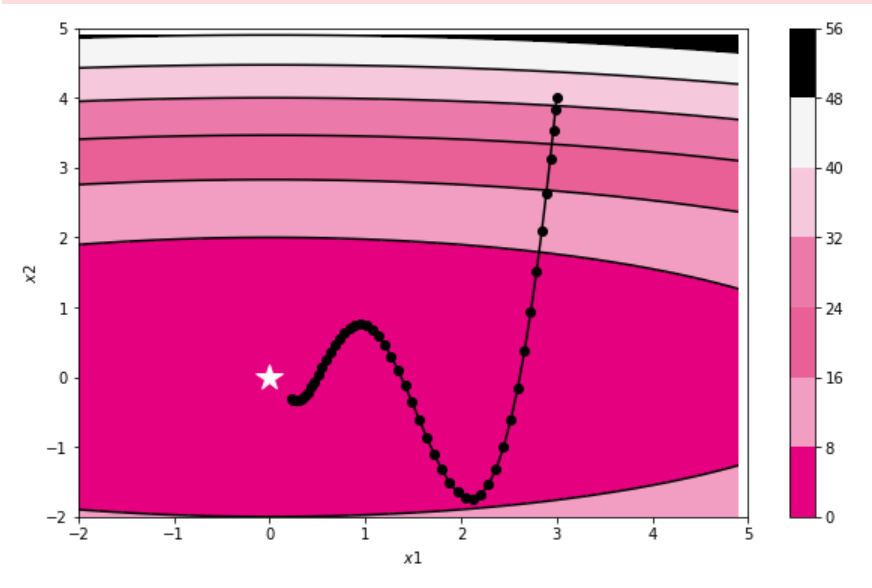
（2）被优化函数

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDictclass SGD:"""随机梯度下降法（Stochastic Gradient Descent）"""def __init__(self, lr=0.01):self.lr = lrdef update(self, params, grads):for key in params.keys():params[key] -= self.lr * grads[key]class Momentum:"""Momentum SGD"""def __init__(self, lr=0.01, momentum=0.9):self.lr = lrself.momentum = momentumself.v = Nonedef update(self, params, grads):if self.v is None:self.v = {}for key, val in params.items():self.v[key] = np.zeros_like(val)for key in params.keys():self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]params[key] += self.v[key]class Nesterov:"""Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""def __init__(self, lr=0.01, momentum=0.9):self.lr = lrself.momentum = momentumself.v = Nonedef update(self, params, grads):if self.v is None:self.v = {}for key, val in params.items():self.v[key] = np.zeros_like(val)for key in params.keys():self.v[key] *= self.momentumself.v[key] -= self.lr * grads[key]params[key] += self.momentum * self.momentum * self.v[key]params[key] -= (1 + self.momentum) * self.lr * grads[key]class AdaGrad:"""AdaGrad"""def __init__(self, lr=0.01):self.lr = lrself.h = Nonedef update(self, params, grads):if self.h is None:self.h = {}for key, val in params.items():self.h[key] = np.zeros_like(val)for key in params.keys():self.h[key] += grads[key] * grads[key]params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)class RMSprop:"""RMSprop"""def __init__(self, lr=0.01, decay_rate=0.99):self.lr = lrself.decay_rate = decay_rateself.h = Nonedef update(self, params, grads):if self.h is None:self.h = {}for key, val in params.items():self.h[key] = np.zeros_like(val)for key in params.keys():self.h[key] *= self.decay_rateself.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)class Adam:"""Adam (http://arxiv.org/abs/1412.6980v8)"""def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):self.lr = lrself.beta1 = beta1self.beta2 = beta2self.iter = 0self.m = Noneself.v = Nonedef update(self, params, grads):if self.m is None:self.m, self.v = {}, {}for key, val in params.items():self.m[key] = np.zeros_like(val)self.v[key] = np.zeros_like(val)self.iter += 1lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)for key in params.keys():self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)def f(x, y):return x ** 2 / 20.0 + y ** 2def df(x, y):return x / 10.0, 2.0 * yinit_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)idx = 1for key in optimizers:optimizer = optimizers[key]x_history = []y_history = []params['x'], params['y'] = init_pos[0], init_pos[1]for i in range(30):x_history.append(params['x'])y_history.append(params['y'])grads['x'], grads['y'] = df(params['x'], params['y'])optimizer.update(params, grads)x = np.arange(-10, 10, 0.01)y = np.arange(-5, 5, 0.01)X, Y = np.meshgrid(x, y)Z = f(X, Y)# for simple contour linemask = Z > 7Z[mask] = 0# plotplt.subplot(2, 2, idx)idx += 1plt.plot(x_history, y_history, 'o-', color="red")plt.contour(X, Y, Z)  # 绘制等高线plt.ylim(-10, 10)plt.xlim(-10, 10)plt.plot(0, 0, '+')plt.title(key)plt.xlabel("x")plt.ylabel("y")plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

结果如下：

由此可知，平滑收敛效果排序为AdaGrad>Adam>Momentum>SGD。

从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？是的，但是他俩的学习率不同，修改学习率为相同值后输出如下：

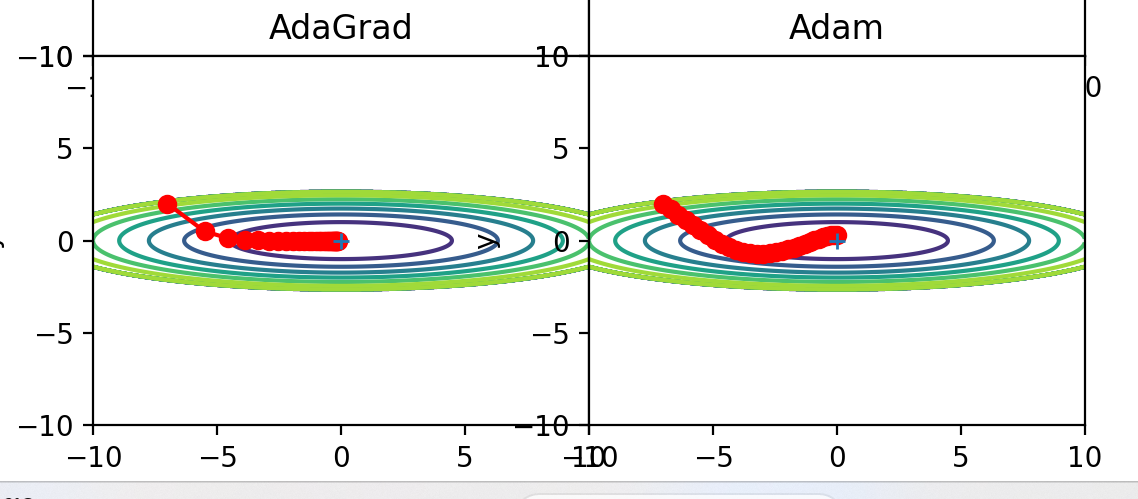
还是ADaGrad效果好。

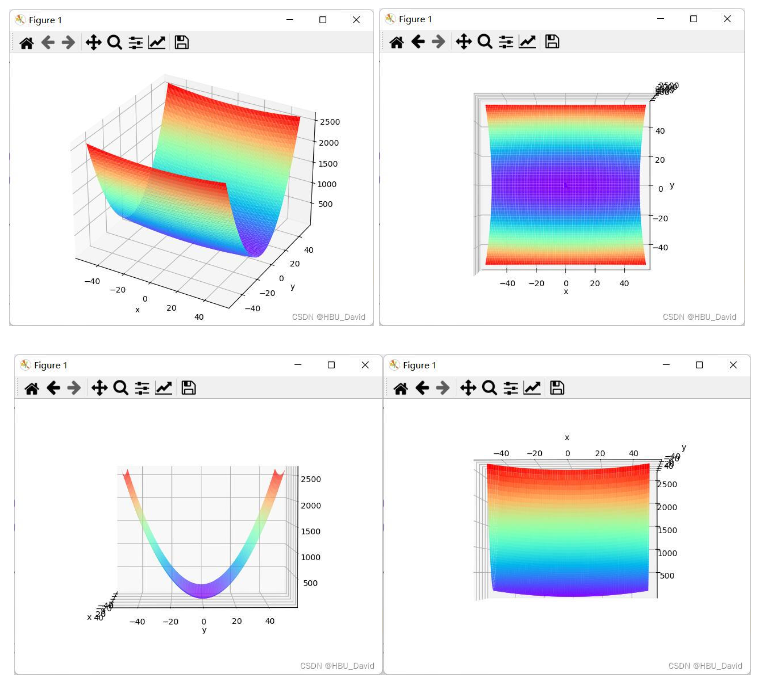
2. 编程实现图6-1，并观察特征

import numpy as np
from matplotlib import pyplot as plt
# 导入 Matplotlib 的 3D 工具包，用于绘制三维图形
from mpl_toolkits.mplot3d import Axes3D# 定义被优化函数 func(x, y) = x * x + 20 * y * y
def func(x, y):return x * x + 20 * y * y# 用于绘制三维曲面图  
def paint_loss_func():# 使用 NumPy 的 linspace 函数在 -50 到 50 的区间上均匀取 100 个数作为 x 和 y 的值x = np.linspace(-50, 50, 100)y = np.linspace(-50, 50, 100)# 使用 NumPy 的 meshgrid 函数生成两个二维数组，这两个数组分别对应 X 和 Y 坐标的网格点X, Y = np.meshgrid(x, y)# 使用之前定义的 func 函数计算每个网格点上的 Z 值，得到一个二维数组 ZZ = func(X, Y)# 创建一个新的画图窗口fig = plt.figure()  # figsize=(10, 10))# 添加一个 3D 子图到图形窗口中，并获取这个子图的 Axes3D 对象ax = Axes3D(fig)# 设置 x 轴和 y 轴的标签plt.xlabel('x')plt.ylabel('y')# 使用 Axes3D 对象的 plot_surface 方法绘制三维曲面图，rstride 和 cstride 参数控制行和列的跨度，cmap 参数设置颜色映射ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')plt.show()
# 调用 paint_loss_func 函数绘制三维曲面图
paint_loss_func()

得到输出结果为：

3. 解释不同轨迹的形成原因

分析各个算法的优缺点。

（1）SGD算法：

SGD的y方向上更新变化很大，而x轴方向上变化小，由于梯度的随机性质，梯度搜索轨迹要很嘈杂（动荡现象），所以会成之字形。如下图【深度学习基础-优化算法详解 - 知乎 (zhihu.com)】

优点：

a）计算速度快：每次只随机选择一个样本来更新模型参数，每次的学习是非常快速的，并且可以进行在线更新。

b）可适用于大规模数据集：SGD的训练速度很快，因此它对于大规模数据集也很适用。

c）可以跳出局部最优：由于SGD每次只考虑一个样本，因此更容易跳出局部最优点，从而找到全局最优解。

缺点：

a）更新具有随机性：每次更新可能不会按照正确的方向进行，会来优化波动(扰动)，如下图：

b）需要调整学习率：由于波动，因此会使得迭代次数（学习次数）增多，即收敛速度变慢，需要调整学习率。选择合适的learning rate比较困难，若设置过大，学习曲线将会剧烈震荡，代价函数值通常会明显增加；太小则学习过程会很缓慢，如果初始学习率太低，那么学习可能会卡在一个相当高的代价值。

（2）AdaGrad算法：

函数的取值高效地向着最小值移动。由于y轴方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整减小更新的步伐。因此y轴方向上的更新程度被减弱，“之”字形的变动程度有所衰减。

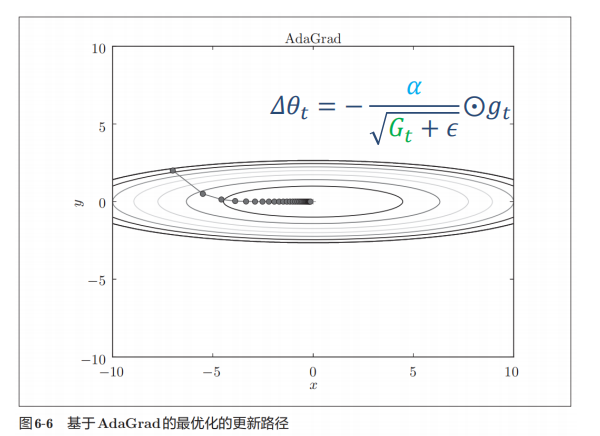
优点：

a）适合于处理稀疏梯度：具有损失最大偏导的参数相应地有一个快速下降的学习率，而具有小偏导的参数在学习率上有相对较小的下降。

b）能够很好的提高SGD的鲁棒性：google便用起来训练大规模神经网络(看片识猫：recognize cats in Youtube videos)。Pennington等[5]在GloVe中便使用Adagrad来训练得到词向量(Word Embeddings), 频繁出现的单词赋予较小的更新，不经常出现的单词则赋予较大的更新。

c）自适应学习率：它能够为每个参数自适应不同的学习速率

缺点：

a）学习率变化：在训练初期分母较小，学习率较大，学习比较快；到后期学习会逐渐减慢。也就是随着迭代次数的增加，学习率逐渐缩小，经过一定次数的迭代没有找到最优点时，学习率已经非常小，很难再继续找到最优点。

b）只能解决凸问题：当应用于非凸函数训练神经网络时，学习可能会到达一个局部是凸碗的区域。

c）需要一个全局的学习率。

（3）RMSprop算法：

RMSprop算法的轨迹图与AdaGrad算法相比：RMSprop的轨迹到后期表现出更加平缓和稳定的学习率变化，更有效地收敛到损失函数的最小值。

优点：

a）有些情况下避免 AdaGrad中学习率不断单调下降，防止过早衰减

b）避免梯度消失和梯度爆炸： 通过对梯度进行归一化，RMSprop有助于保持稳定的优化过程

c）收敛速度快且平稳：在参数空间更为平缓的方向，会取得更大的进步（因为平缓，所以历史梯度平方和较小，对应学习下降的幅度较小），并且能够使得陡峭的方向变得平缓，从而加快训练速度。

缺点：

a）依然依赖一个全局学习率

b）需要调整超参数:如衰减率和学习率.

（4）Momentum动量法：

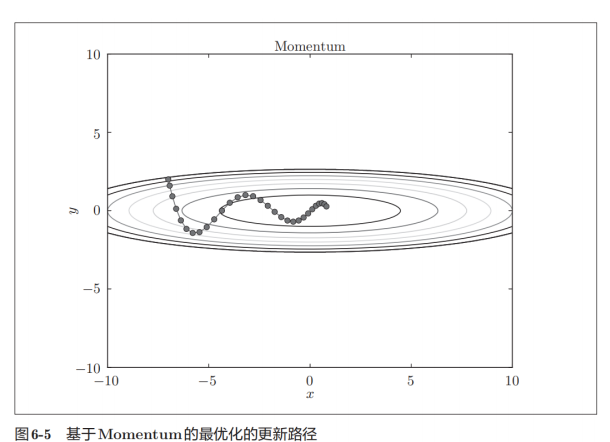
和SGD相比，当参数更新幅度变小，动量法会起到减速作用-->增加稳定性，减少震荡可更快朝x轴方向靠近，减弱“之”字形变动程度；同时当参数更新幅度大时，动量法会加速。如下图：

优点：

a）增强稳定性，训练速度快：在更新时在一定程度上会考虑之前更新的方向，同时利用当前batch的梯度微调最终的结果，这样可以在一定程度上增加稳定性，从而更快的学习。

b）抑制震荡，比较稳定：可以处理处理高曲率、小但一致的梯度，或是带噪声的梯度

c）还有一定摆脱局部最优的能力。

缺点：

引入新的超参数

（5）Nesterov算法：

从山顶往下滚的球会盲目地选择斜坡。更好的方式应该是在遇到倾斜向上之前应该减慢速度。该算法是对动量法的改进，不仅仅根据当前梯度调整位置，而是根据当前动量在预期的未来位置计算梯度。所以，算法可以相应地调整更新，避免在使用梯度下降时可能出现的振荡，图中的轨迹呈现出更加平滑、更有方向性的路径朝向最优点。

优点：

a）相对于标准梯度下降，更快地收敛到最小值。

b）考虑了动量，有助于避免振荡。

缺点：

需要调整学习率和动量参数。

（6）Adam算法

Adam的收敛轨迹图和其他的相比，明显要稳定，基本上是呈直线，或者前期收敛幅度较大，后期逐渐平稳，朝着最优点不断移动。Adam算法结合了动量法和 RMSprop 算法，不仅何以自适应调整学习率，收敛速度快，并且参数更新更加平稳。

优点：

a）超参数具有很好的解释性，且通常无需调整或仅需很少的微调

b）更新的步长能够被限制在大致的范围内（初始学习率），能自然地实现步长退火过程（自动调整学习率）

c）适用于不稳定目标函数、梯度稀疏或梯度存在很大噪声的问题

缺点：

在非凸函数上可能不会收敛到全局最小值。

参考：

【干货】深度学习必备：随机梯度下降（SGD）优化算法及可视化 (qq.com)

(54 封私信 / 82 条消息) 随机梯度下降算法的优点和缺点分别是什么？ - 知乎 (zhihu.com)

各优化算法的优缺点整理_智能优化算法的优缺点-CSDN博客

深度学习基础-优化算法详解 - 知乎 (zhihu.com)

4.总结

本次作业主要学习的各种优化算法，优化算法的目的主要有两个：一是调整学习率，使得优化更加稳定；二是梯度估计修正，优化训练速度。

所以参照上图可以看到，调整学习率中可以通过学习率衰减【又称学习率退火，具体函数使用可以参考下图】

学习率预热，也就是为了提高训练稳定性，最初几轮迭代时，采用比较小的学习率，等梯度下降到一定程度后，恢复到初始的学习率. 预热过程结束，再选择一种学习率衰减方法来逐渐降低学习率。

周期性学习率调整，也就是在周期中周期性的增大学习率，有两种常见的方法如下：

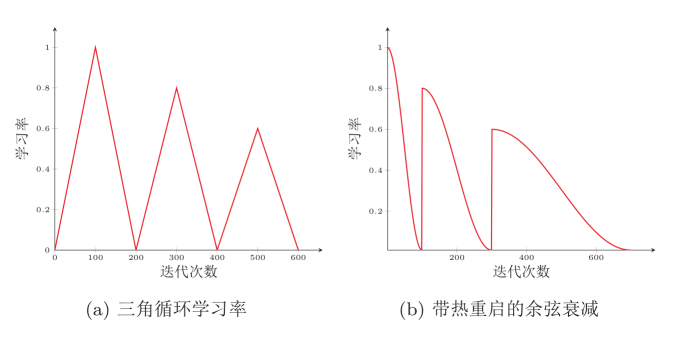
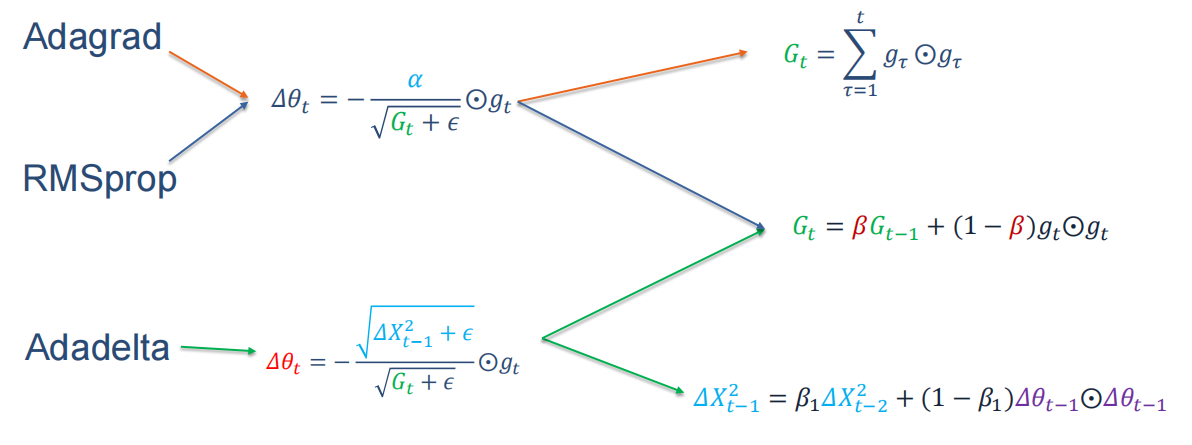
自适应学习率【自适应地调整每个参数的学习率.】，在前边都提到了，有AdaGrad算法、RMSprop 算法和AdaDelta 算法。公式记法老师也给了对比的，如下图：

也可以看到，RMSprop算法与AdaGrad算法区别在于更新梯度上，也就是由平方和改为了梯度𝑔𝑔𝑡𝑡平方的指数衰减移动平均【逐渐遗忘以前的梯度情况，更加关注目前梯度】，目的是缓解学习率衰减。

而Adadelta与RMSprop算法类似，它引入每次参数更新差值𝜟𝜽平方的指数衰减权移动平均．可以看到前两个都需要依赖全局学习率，需要给出一个最初的学习率，但是这个算法不需要：AdaDelta动态确定学习率𝛼，不需要提前设置。

而再通过梯度估计修正来优化算法中，主要学习了动量法和Nesterov加速梯度。这两个算法的优缺点前边也已经介绍了，更新公式如下：

关于Adam算法，Adam算法 ≈ 动量法 + RMSprop

其实就可以看出，一方面它进行了梯度估计修正方面的改良-->用之前积累动量替代真正的梯度。另一方面，还可以自适应学习率-->自适应地调整每个参数的学习率，也就是可以根据不同参数的收敛情况分别设置学习率。

最后下图总结：

以上图片均是参考老师PPT内容。

【23-24 秋学期】NNDL 作业12 优化算法2D可视化-CSDN博客

神经网络与深度学习（八）网络优化与正则化（3）不同优化算法比较_神经网络的网络优化与正则化方法-CSDN博客

兮希NGC2237_深度学习,BP-CSDN博客