目录
主要内容
集合的基本概念
集合的基本运算
集合恒等式
初级运算
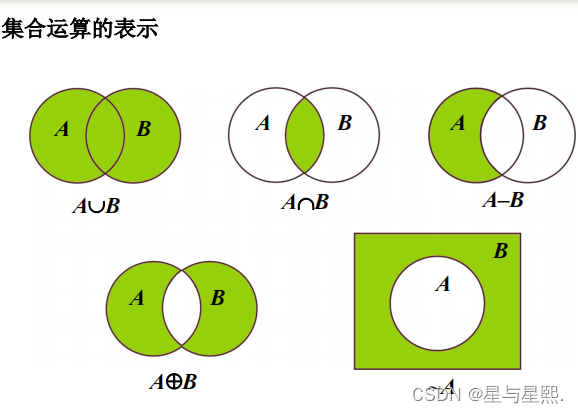
文氏图
集合的广义并与广义交
广义运算的性质
例1 A={{a},{a,b}}
集合算律
例2 判断下列命题是否为真
例3 设
例4 判断以下命题的真假,并说明理由.
解题思路
主要内容
集合的基本概念
属于、包含幂集、空集文氏图等集合的基本运算
并、交、补、差等集合恒等式
集合运算的算律、恒等式的证明方法
1. 集合定义
集合没有精确的数学定义理解:由离散个体构成的整体称为 集合 ,称这些个体为集 合的 元素 常见的数集: N , Z , Q, R, C 等分别表示自然数、整数、有 理数、实数、复数集合2. 集合表示法枚举法 ---- 通过列出全体元素来表示集合谓词表示法 ---- 通过谓词概括集合元素的性质实例:枚举法 自然数集合 N={0,1,2,3,…}谓词法 S ={ x | x 是实数, x 2 − 1=0}
集合与集合之间的关系:⊆, =, ⊈, ≠, ⊂, ⊄
定义 6.1 A ⊆ B ⇔ ∀ x ( x ∈ A → x ∈ B )定义 6.2 A = B ⇔ A ⊆ B ∧ B ⊆ A定义 6.3 A ⊂ B ⇔ A ⊆ B ∧ A ≠ BA ⊈ B ⇔ ∃ x ( x ∈ A ∧ x ∉ B )思考: ≠ 和 ⊄ 的定义注意 :∈ 和 ⊆ 是不同层次的问题
定义 6.4 空集 ∅ :不含有任何元素的集合实例: { x | x ∈ R ∧ x 2 +1=0 }定理 6.1 空集是任何集合的子集。证 对于任意集合 A ,∅⊆ A ⇔ ∀ x ( x ∈∅→ x ∈ A ) ⇔ T ( 恒真命题 )推论 ∅ 是惟一的定义 6.6 全集 E :包含了所有集合的集合全集具有相对性:与问题有关,不存在绝对的全集定义 6.5 幂集 : P ( A )={ x | x ⊆ A }实例: P ( ∅ )={ ∅ }, P ({ ∅ })={ ∅ ,{ ∅ }}计数:如果 | A |= n ,则 | P ( A )|=2 n
初级运算
集合的基本运算有定义 6.7 并 A ∪ B = { x | x ∈ A ∨ x ∈ B }交 A ∩ B = { x | x ∈ A ∧ x ∈ B }相对补 A − B = { x | x ∈ A ∧ x ∉ B }定义 6.8 对称差 A ⊕ B = ( A − B ) ∪ ( B − A )定义 6.9 绝对补 ∼ A = E − A简单来说A-B 就是 属于A不属于BE为定义上的全集~A属于E不属于A
文氏图
并和交运算可以推广到有穷个集合上即A 1 ∪ A 2 ∪ … ∪ A n = { x | x ∈ A 1 ∨ x ∈ A 2 ∨ … ∨ x ∈ A n }A 1 ∩ A 2 ∩ … ∩ A n = { x | x ∈ A 1 ∧ x ∈ A 2 ∧ … ∧ x ∈ A n }A ⊆ B ⇔ A − B = ∅A ∩ B = ∅ ⇔ A − B = A
集合的广义并与广义交
定义 6.10广义并 ∪ A = { x | ∃ z ( z ∈ A ∧ x ∈ z )}广义交 ∩ A = { x | ∀ z ( z ∈ A → x ∈ z )}实例∪ {{1}, {1,2}, {1,2,3}}={1,2,3}∩ {{1}, {1,2}, {1,2,3}}={1}∪ {{ a }}={ a } , ∩ {{ a }}={ a }∪ { a }= a , ∩ { a }= a广义运算的性质
(1) ∪∅ = ∅ , ∩∅ 无意义(2) 单元集 { x } 的广义并和广义交都等于 x(3) 广义运算减少集合的层次(括弧减少一层)(4) 广义运算的计算:一般情况下可以转变成初级运算∪ { A 1 , A 2 , … , A n }= A 1 ∪ A 2 ∪ … ∪ A n∩ { A 1 , A 2 , … , A n }= A 1 ∩ A 2 ∩ … ∩ A n引入广义运算的意义可以表示无数个集合的并、交运算,例如∪ {{ x } | x ∈ R}=R这里的 R 代表实数集合简单来说广义并就是所有集合并在一起广义交就是所有集相交在一起
运算的优先权规定1类运算:初级运算 ∪ , ∩ , − , ⊕ ,优先顺序由括号确定2 类运算:广义运算和 ∼ 运算,运算由右向左进行混合运算: 2 类运算优先于 1 类运算
例1 A={{a},{a,b}}
计算 ∩∪ A ∪ ( ∪∪ A −∪∩ A ).解:∩∪ A ∪ ( ∪∪ A −∪∩ A )= ∩ { a , b } ∪ ( ∪ { a , b } −∪ { a })= ( a ∩ b ) ∪ (( a ∪ b ) − a )= ( a ∩ b ) ∪ ( b − a ) = b
集合算律
只涉及一个运算的算律交换律 、 结合律 、 幂等律
A∪E=E A∩E=A ∼E=∅
例2 判断下列命题是否为真
(1) ∅⊆∅(2) ∅∈∅(3) ∅⊆ { ∅ }(4) ∅∈ { ∅ }(5) { a , b } ⊆ { a , b , c , { a , b , c }}(6) { a , b } ∈ { a , b , c , { a , b }}(7) { a , b } ⊆ { a , b , {{ a , b }}}(8) { a , b } ∈ { a , b , {{ a , b }}}解(1)真,空集是空集的子集,因为空集是任何集合的子集(2)假,空集元素属于空集这个集合,空集没有任何元素(3)真,空集是任何集合的子集(4)真,集合中存在空集元素(5)真,{ a , b }为{ a , b , c , { a , b , c }}的子集(6)真, { a , b , c , { a , b}}中有{ a , b }这个元素(7)真,{ a , b }为{ a , b , {{ a , b }}}的子集(8)假, { a , b , {{ a , b}}}中没有{ a , b }这个元素,只有元素a,b,{{ a , b}}
例3 设
S 1 ={1, 2, … , 8, 9} , S 2 ={2, 4, 6, 8}S 3 ={1, 3, 5, 7, 9} S 4 ={3, 4, 5}S 5 ={3, 5}确定在以下条件下 X 是否与 S 1 ,…, S 5 中某个集合相等?如果是,又与哪个集合相等?( 1 )若 X ∩ S 5 = ∅( 2 )若 X ⊆ S 4 但 X ∩ S 2 = ∅( 3 )若 X ⊆ S 1 且 X ⊈ S 3( 4 )若 X − S 3 = ∅( 5 )若 X ⊆ S 3 且 X ⊈ S解(1) 和 S 5 不交的子集不含有 3 和 5 ,因此 X = S 2(2) S 4 的子集只能是 S 4 和 S 5 . 由于与 S 2 不交,不能含有偶数, 因此 X = S 5(3) S 1 , S 2 , S 3 , S 4 和 S 5 都是 S 1 的子集,不包含在 S 3 的子集含有 偶数,因此 X = S 1 , S 2 或 S 4(4) X − S 3 = ∅ 意味着 X 是 S 3 的子集,因此 X = S 3 或 S 5(5) 由于 S 3 是 S 1 的子集,因此这样的 X 不存在
例4 判断以下命题的真假,并说明理由.
( 1 ) A − B = A ⇔ B = ∅( 2 ) A − ( B ∪ C ) = ( A − B ) ∩ ( A − C )( 3 ) A ⊕ A = A( 4 )如果 A ∩ B = B ,则 A = E .( 5 ) A = { x } ∪ x ,则 x ∈ A 且 x ⊆ A .解题思路
先将等式化简或恒等变形查找集合运算的相关的算律,如果与算律相符,结果为真注意以下两个重要的充要条件A − B = A ⇔ A ∩ B = ∅A − B = ∅ ⇔ A ⊆ B ⇔ A ∪ B = B ⇔ A ∩ B = A如果与条件相符,则命题为真 .如果不符合算律,也不符合上述条件,可以用文氏图表示集合,看看命题是否成立 . 如果成立,再给出证明 .试着举出反例,证明命题为假解(1) B = ∅ 是 A − B = A 的充分条件,但不是必要条件 . 当 B 不空但 是与 A 不交时也有 A − B = A(2) 这是 DM 律,命题为真(3) 不符合算律,反例如下:A ={1} , A ⊕ A = ∅ ,但是 A ≠∅(4) 命题不为真 . A ∩ B = B 的充分必要条件是 B ⊆ A ,不是 A = E(5) 命题为真,因为 x 既是 A 的元素,也是 A 的子集