前言
Emm,由于上一篇笔记的字数超过了要求(这还是第一次- -),就把后续内容放到这篇笔记里面了,公式的标号仍然不变,上一篇笔记的连接在这:无约束优化问题求解(4):牛顿法
SR1, DFP, BFGS之间的关系
首先给出如下SMW公式:

考虑到 B k B_k Bk 才是对Hessian矩阵的近似,如果我们能够知道每步对 Hessian矩阵的近似情况,那么将对收敛性分析有着很大的帮助.
SR1的有递推公式为 H k + 1 = H k + ( s k − H k y k ) ( s k − H k y k ) T ( s k − H k y k ) T y k H_{k+1}=H_k+\frac{(s_k-H_ky_k)(s_k-H_ky_k)^T}{(s_k-H_ky_k)^Ty_k} Hk+1=Hk+(sk−Hkyk)Tyk(sk−Hkyk)(sk−Hkyk)T两边取逆,使用SMW公式,可以得到SR1中, B k B_k Bk 的迭代式
B k + 1 = B k + ( y k − B k s k ) ( y k − B k s k ) T ( y k − B k s k ) T s k B_{k+1}=B_k+\frac{(y_k-B_ks_k)(y_k-B_ks_k)^T}{(y_k-B_ks_k)^Ts_k} Bk+1=Bk+(yk−Bksk)Tsk(yk−Bksk)(yk−Bksk)T可以发现,结果就是将 s k s_k sk 和 y k y_k yk 交换,把 B k B_k Bk 和 H k H_k Hk 交换。
因此,我们说SR1是自对偶的。
再看看DFP和BFGS迭代公式两边取逆后的结果:
D F P : H k + 1 = H k + s k s k T s k T y k − H k y k y k T H k y k T H k y k B k + 1 = B k + ( 1 + s k T B k s k s k T y k ) y k y k T s k T y k − ( y k s k T B k + B k s k y k T s k T y k ) B F G S : H k + 1 = H k + ( 1 + y k T H k y k s k T y k ) s k s k T s k T y k − ( s k y k T H k + H k y k s k T s k T y k ) B k + 1 = B k + y k y k T y k T s k − B k s k s k T B k s k T B k s k \begin{aligned} \mathrm{DFP}:H_{k+1}& =H_k+\frac{s_ks_k^T}{s_k^Ty_k}-\frac{H_ky_ky_k^TH_k}{y_k^TH_ky_k} \\ B_{k+1}& =B_k+\left(1+\frac{s_k^TB_ks_k}{s_k^Ty_k}\right)\frac{y_ky_k^T}{s_k^Ty_k}-\left(\frac{y_ks_k^TB_k+B_ks_ky_k^T}{s_k^Ty_k}\right) \\ \mathrm{BFGS}:H_{k+1}& =H_k+\left(1+\frac{y_k^TH_ky_k}{s_k^Ty_k}\right)\frac{s_ks_k^T}{s_k^Ty_k}-\left(\frac{s_ky_k^TH_k+H_ky_ks_k^T}{s_k^Ty_k}\right) \\ B_{k+1}& =B_k+\frac{y_ky_k^T}{y_k^Ts_k}-\frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k} \end{aligned} DFP:Hk+1Bk+1BFGS:Hk+1Bk+1=Hk+skTykskskT−ykTHkykHkykykTHk=Bk+(1+skTykskTBksk)skTykykykT−(skTykykskTBk+BkskykT)=Hk+(1+skTykykTHkyk)skTykskskT−(skTykskykTHk+HkykskT)=Bk+ykTskykykT−skTBkskBkskskTBk可以发现只要 s k ↔ y k , B k ↔ H k s_{k}\leftrightarrow y_{k},B_{k}\leftrightarrow H_{k} sk↔yk,Bk↔Hk,就可以在DFP和BFGS公式之间相互转换。因此,我们说DFP和BFGS互为对偶的。
设需要优化的目标函数如下:
min f ( x ) = ∑ i = 1 4 r i ( x ) 2 \min f(x)=\sum_{i=1}^4r_i(x)^2 minf(x)=i=1∑4ri(x)2其中 r 2 i − 1 ( x ) = 10 ( x 2 i − x 2 i − 1 2 ) , r 2 i ( x ) = 1 − x 2 i − 1 r_{2i-1}(x)=10(x_{2i}-x_{2i-1}^2),r_{2i}(x)=1-x_{2i-1} r2i−1(x)=10(x2i−x2i−12),r2i(x)=1−x2i−1 , x ∈ R 4 x\in\mathbb{R}^4 x∈R4 , x k x_k xk 代表向量 x x x 的第 k k k 个维度上的元素。
我们可以看出上述的优化问题的最优点为 ( 1 , 1 , 1 , 1 ) T (1,1,1,1)^T (1,1,1,1)T(可能有读者想知道怎么看出来的,只需要对每个分量求导,并令每个分量的一阶偏导数 ∂ f ∂ x i = 0 \frac{\partial f}{\partial x_i}=0 ∂xi∂f=0,求解出来的点便是可能的极值点) , 取迭代初值为 x 0 = ( 2 , 0 , 3 , 4 ) T x_0=(2,0,3,4)^T x0=(2,0,3,4)T 。我们首先先实现上述的函数,我通过一个函数获取一个映射 f : f: f:
from scipy.optimize import fmin_powell, fmin_bfgs, fmin_cg, minimize, SR1
import numpy as np
import matplotlib.pyplot as plt
# 定义函数
def r(i, x):if i % 2 == 1:return 10 * (x[i] - x[i - 1] ** 2) # 因为ndarray数组的index是从0开始的, i多减一个else:return 1 - x[i - 2]
def f(m):def result(x):return sum([r(i, x) ** 2 for i in range(1, m + 1)])return result # 返回函数值
为了观察拟牛顿法运行过程中迭代点的下降情况,我们需要计算损失的函数如下:
# 获取retall的每个点的值损失|f(x) - f(x^*)|
def getLosses(retall, target_point, func):""":param retall: 存储迭代过程中每个迭代点的列表,列表的每个元素时一个ndarray对象:param target_point: 最优点,是ndarray对象:param func: 优化函数的映射f:return: 返回一个列表,代表retall中每个点到最优点的欧氏距离"""losses = []for point in retall:# 对于每一个迭代点的列表做循环losses.append(np.abs(func(target_point) - func(point))) #绝对值做损失return losses
scipy.optimize子库中的许多执行拟牛顿法的算子提供了call_back参数,该参数要求传入一个函数对象,在拟牛顿每步迭代完后,传入的call_back函数会被调用。由于使用SR1法的算子minimize无法返回迭代过程中的每一个迭代点(也就是retall),于是我们需要call_back函数来将迭代完的点传入外部的列表,从而获取SR1的retall。除此之外,我们可以使用call_back函数来指定迭代停止的条件。
我们编写一个返回函数对象的函数,它会根据我们传入参数的不同返回不同的call_back函数:
sr1_losses = [] # 存储SR1的retall的列表
func = f(4) # 获取需要优化的函数
# 通过callback方法来添加迭代的停止条件
def getCallback(func, target_point, ftol, retall):""":param func: 优化目标的函数:param target_point: 目标收敛点:param ftol: 收敛条件:|f(x) - f(x^*)| < ftol时,迭代停止:param retall: 是否存储迭代信息:param extern_retall: 如果retall为True, 填入一个列表,迭代信息会存在这个列表中:return: call_back函数对象"""# 定义result函数def result(xk, state=None):if retall:global func, sr1_losses # 对于SR1而言,需要声明全局变量来返回call_back对象loss = np.abs(func(target_point) - func(xk))if loss < ftol:return Trueelse:if retall: # 如果是SR1算法,则返回一个布尔值sr1_losses.append(loss)return Falsereturn result # 如果不是SR1算法,则返回一个call_back对象
为了方便可视化,我们将数据可视化的逻辑封装到一个函数中:
# 绘制下降曲线
def plotDownCurve(dpi, losses, labels, xlabel=None, ylabel=None, title=None, grid=True):plt.figure(dpi=dpi)for loss, label in zip(losses, labels):plt.plot(loss, label=label)plt.xlabel(xlabel, fontsize=12)plt.ylabel(ylabel, fontsize=12)plt.title(title, fontsize=18)plt.yscale("log")plt.grid(grid)plt.legend()
接着我们定义一下迭代初值、最优点和终止条件的阈值 ϵ \epsilon ϵ ( ∣ f ( x k + 1 ) − f ( x k ) ∣ < ϵ |f(x_{k+1})-f(x_k)|<\epsilon ∣f(xk+1)−f(xk)∣<ϵ 时,迭代停止) 并获取三个拟牛顿法需要的 call_back函数。
x_0 = np.array([2,0,3,4]) # 迭代初值
target_point = np.array([1,1,1,1], dtype="float32") # 最优点
FTOL = 1e-8 # 终止阈值
sr1_callback = getCallback(func, target_point, ftol=FTOL, retall=True)
dfp_callback = getCallback(func, target_point, ftol=FTOL, retall=False)
bfgs_callback = getCallback(func, target_point, ftol=FTOL, retall=False)
下面使用minimum,fmin_powell,fmin_bfgs来实现三种拟牛顿法的迭代,并把DFP和BFGS的retall存入列表中。
# retall 是迭代点列,minimum是最终迭代点
minimum = minimize(fun=f(4), x0=x_0, # 通过minimize函数执行SR1,根据内嵌的callback填充loss,并返回OptimizerResult对象method="trust-constr",hess=SR1(),callback=sr1_callback)
dfp_minimum, dfp_retall = fmin_powell(func=func, x0=x_0, retall=True,disp=False,callback=dfp_callback)
dfp_losses = getLosses(dfp_retall, target_point, func=func)
bfgs_minimum, bfgs_retall = fmin_bfgs(f=func, x0=x_0,retall=True,disp=False,callback=bfgs_callback)
bfgs_losses = getLosses(bfgs_retall, target_point, func=func)
我们可以调整plt画布的分辨率,设置一下各个轴的名称,然后将它可视化出来:
plotDownCurve(dpi=150, losses=[sr1_losses, dfp_losses, bfgs_losses],labels=["SR1", "DFP", "BFGS"],xlabel="#iter", ylabel="value of $|f(x) - f(x^*)|$",title="losses curve of SR1, DFP and BFGS")
plt.show()
运行结果:
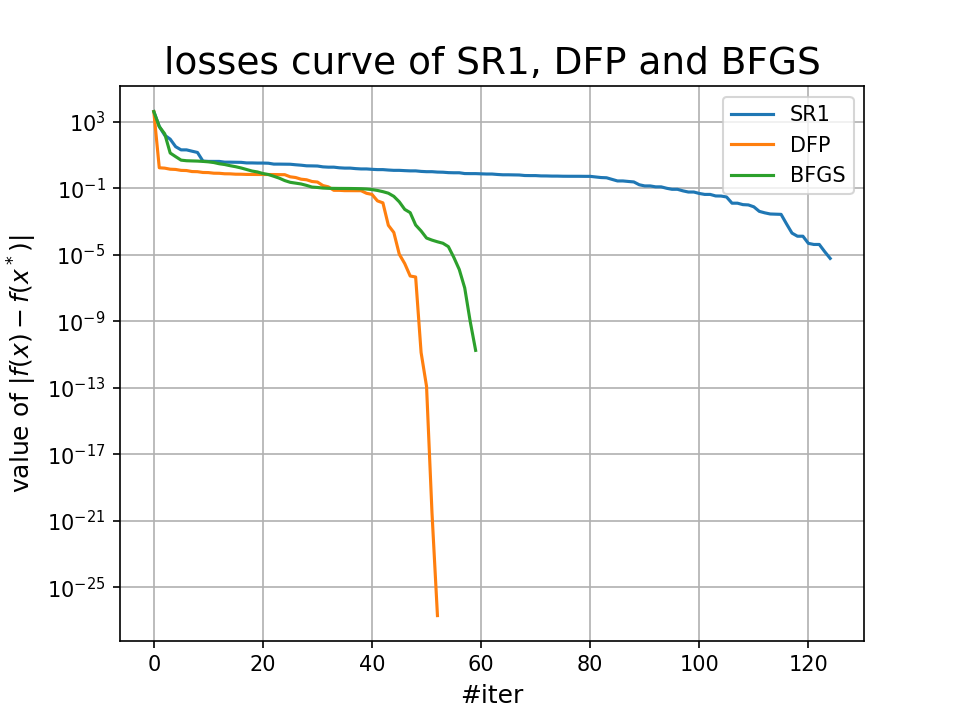
我们还可以查看三种方法得到的最优点和它们具体的迭代次数:
print(f"SR1\t最终迭代点:{minimum.x.tolist()}, 共经历{minimum.cg_niter}次迭代")
print(f"DFP\t最终迭代点:{dfp_minimum}, 共经历{len(dfp_losses)}次迭代")
print(f"BFGS\t最终迭代点:{bfgs_minimum}, 共经历{len(bfgs_losses)}次迭代")
运行结果:
SR1 最终迭代点:[1.0000311207482149, 1.0000594706577797, 0.999965823924486, 0.999928146607472], 共经历418次迭代
DFP 最终迭代点:[1. 1. 1. 1.], 共经历53次迭代
BFGS 最终迭代点:[0.99999614 0.99999229 0.99999844 0.99999693], 共经历60次迭代
BB方法
在拟 Newton 法中,我们寻找对称矩阵 B k + 1 B_{k+1} Bk+1 使得 B k + 1 s k = y k . B_{k+1}s_k=y_k. Bk+1sk=yk. Barzilai 和 Borwein 提出:取 B k + 1 = α − 1 I B_{k+1}=\alpha^{-1}I Bk+1=α−1I.然而,这样的选取一般不能满足 B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1sk=yk.因此,BB 方法将该等式条件改为
α k + 1 : = argmin α > 0 ∥ α − 1 s k − y k ∥ 2 . \alpha_{k+1}:=\underset{\alpha>0}{\operatorname*{argmin}}\|\alpha^{-1}s_k-y_k\|_2. αk+1:=α>0argmin∥α−1sk−yk∥2.解之得 α k + 1 = s k T s k / ( s k T y k ) \alpha_{k+1}=s_k^Ts_k/(s_k^Ty_k) αk+1=skTsk/(skTyk).类似于拟 Newton 法使用 d k + 1 = − B k + 1 − 1 ∇ f ( x k + 1 ) d_{k+1}=-B_{k+1}^{-1}\nabla f(x_{k+1}) dk+1=−Bk+1−1∇f(xk+1) 为搜索方向,BB 算法采用
d k + 1 : = ( α k + 1 − 1 I ) − 1 ∇ f ( x k + 1 ) = α k + 1 ∇ f ( x k + 1 ) . d_{k+1}:=(\alpha_{k+1}^{-1}I)^{-1}\nabla f(x_{k+1})=\alpha_{k+1}\nabla f(x_{k+1}). dk+1:=(αk+1−1I)−1∇f(xk+1)=αk+1∇f(xk+1).
所以,BB 算法的搜索方向仍是负梯度方向. 由于上面已经考虑了步长,所以 BB 算法不再搜索步长. 这样我们得到如下的迭代公式 x k + 1 = x k − α k ∇ f ( x k ) , α k = s k − 1 T s k − 1 s k − 1 T y k − 1 x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ts_{k-1}}{s_{k-1}^Ty_{k-1}} xk+1=xk−αk∇f(xk),αk=sk−1Tyk−1sk−1Tsk−1类似地,我们将条件 H k + 1 y k = s k H_{k+1}y_k=s_k Hk+1yk=sk 替换成
α k + 1 : = a r g m i n α > 0 ∥ α y k − s k ∥ 2 . \alpha_{k+1}:=\mathop{\mathrm{argmin}}_{\alpha>0}\|\alpha y_k-s_k\|_2. αk+1:=argminα>0∥αyk−sk∥2.
解之得 α k + 1 = s k T y k / ( y k T y k ) \alpha_{k+1}=s_k^Ty_k/(y_k^Ty_k) αk+1=skTyk/(ykTyk). 从而得到如下迭代公式
x k + 1 = x k − α k ∇ f ( x k ) , α k = s k − 1 T y k − 1 y k − 1 T y k − 1 . x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}}. xk+1=xk−αk∇f(xk),αk=yk−1Tyk−1sk−1Tyk−1.公式 x k + 1 = x k − α k ∇ f ( x k ) , α k = s k − 1 T s k − 1 s k − 1 T y k − 1 x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ts_{k-1}}{s_{k-1}^Ty_{k-1}} xk+1=xk−αk∇f(xk),αk=sk−1Tyk−1sk−1Tsk−1 和 x k + 1 = x k − α k ∇ f ( x k ) , α k = s k − 1 T y k − 1 y k − 1 T y k − 1 x_{k+1}=x_k-\alpha_k\nabla f(x_k),\quad\alpha_k=\frac{s_{k-1}^Ty_{k-1}}{y_{k-1}^Ty_{k-1}} xk+1=xk−αk∇f(xk),αk=yk−1Tyk−1sk−1Tyk−1 分别称为 BB1 公式和 BB2 公式,为区别起见,分别将它们对应的步长 α k \alpha_k αk 记为 α k B B 1 \alpha_k^\mathrm{BB1} αkBB1 和 α k B B 2 \alpha_k^\mathrm{BB2} αkBB2,即 α k B B 1 = s k − 1 T s k − 1 s k − 1 T y k − 1 , α k B B 2 = s k − 1 T y k − 1 y k − 1 T y k − 1 . \alpha_{k}^{\mathrm{BB}1}=\frac{s_{k-1}^{T}s_{k-1}}{s_{k-1}^{T}y_{k-1}},\quad\alpha_{k}^{\mathrm{BB}2}=\frac{s_{k-1}^{T}y_{k-1}}{y_{k-1}^{T}y_{k-1}}. αkBB1=sk−1Tyk−1sk−1Tsk−1,αkBB2=yk−1Tyk−1sk−1Tyk−1.特别若目标函数为 f ( x ) = 1 2 x T A x + b T x f(x)=\frac12x^TAx+b^Tx f(x)=21xTAx+bTx, 其中 A A A 为对称正定矩阵, b ∈ R n b\in\mathbb{R}^n b∈Rn, 计算可得
s k − 1 = − α k − 1 ∇ f ( x k − 1 ) , y k − 1 = A s k − 1 = − α k − 1 A ∇ f ( x k − 1 ) s_{k-1}=-\alpha_{k-1}\nabla f(x_{k-1}),\quad y_{k-1}=As_{k-1}=-\alpha_{k-1}A\nabla f(x_{k-1}) sk−1=−αk−1∇f(xk−1),yk−1=Ask−1=−αk−1A∇f(xk−1)从而
α k BB 1 = ∇ f ( x k − 1 ) T ∇ f ( x k − 1 ) ∇ f ( x k − 1 ) T A ∇ f ( x k − 1 ) , α k BB 2 = ∇ f ( x k − 1 ) T A ∇ f ( x k − 1 ) ∇ f ( x k − 1 ) T A 2 ∇ f ( x k − 1 ) , \alpha_{k}^{\text{BB}1}=\frac{\nabla f(x_{k-1})^T\nabla f(x_{k-1})}{\nabla f(x_{k-1})^TA\nabla f(x_{k-1})},\quad\alpha_{k}^{\text{BB}2}=\frac{\nabla f(x_{k-1})^TA\nabla f(x_{k-1})}{\nabla f(x_{k-1})^TA^2\nabla f(x_{k-1})}, αkBB1=∇f(xk−1)TA∇f(xk−1)∇f(xk−1)T∇f(xk−1),αkBB2=∇f(xk−1)TA2∇f(xk−1)∇f(xk−1)TA∇f(xk−1),易见,此时有 α k B B 1 = α k S D , α k B B 2 = α k M D \alpha_k^\mathrm{BB1}=\alpha_k^\mathrm{SD},\:\alpha_k^\mathrm{BB2}=\alpha_k^\mathrm{MD} αkBB1=αkSD,αkBB2=αkMD, 其中, α k S D \alpha_k^\mathrm{SD} αkSD 表示最速下降法之精确搜索的步长 α k M D \alpha_k^\mathrm{MD} αkMD 称为最小梯度法的步长,因为它满足
α k M D = argmin α > 0 ∥ ∇ f ( x k − α ∇ f ( x k ) ) ∥ 2 = ∇ f ( x k ) T A ∇ f ( x k ) ∇ f ( x k ) T A 2 ∇ f ( x k ) . \alpha_k^{\mathrm{MD}}=\underset{\alpha>0}{\operatorname*{argmin}}\|\nabla f(x_k-\alpha\nabla f(x_k))\|_2=\frac{\nabla f(x_k)^TA\nabla f(x_k)}{\nabla f(x_k)^TA^2\nabla f(x_k)}. αkMD=α>0argmin∥∇f(xk−α∇f(xk))∥2=∇f(xk)TA2∇f(xk)∇f(xk)TA∇f(xk).
上面这些证明我就贴在这水个字数,我是看不懂的- -
Reference
本笔记的代码部分来源于下篇文章:
最优化方法复习笔记(四)拟牛顿法与SR1,DFP,BFGS三种拟牛顿算法的推导与代码实现