一、题目
1、题目描述
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标
(i, j)处的苹果树有|i| + |j|个苹果。你将会买下正中心坐标是
(0, 0)的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。给你一个整数
neededApples,请你返回土地的 最小周长 ,使得 至少 有neededApples个苹果在土地 里面或者边缘上。
|x|的值定义为:
- 如果
x >= 0,那么值为x- 如果
x < 0,那么值为-x
2、接口描述
class Solution {
public:long long minimumPerimeter(long long neededApples) {}
};3、原题链接
1954. 收集足够苹果的最小花园周长
二、解题报告
1、思路分析
每个位置是|i| + |j|个苹果,而且限制区域为以原点为中心的正方形,那么一定是有数学规律的。
其实可以分为四个数目相等的区域,为什么呢?
可以由|x| + |y| = k的函数图像得知,也可以观察发现
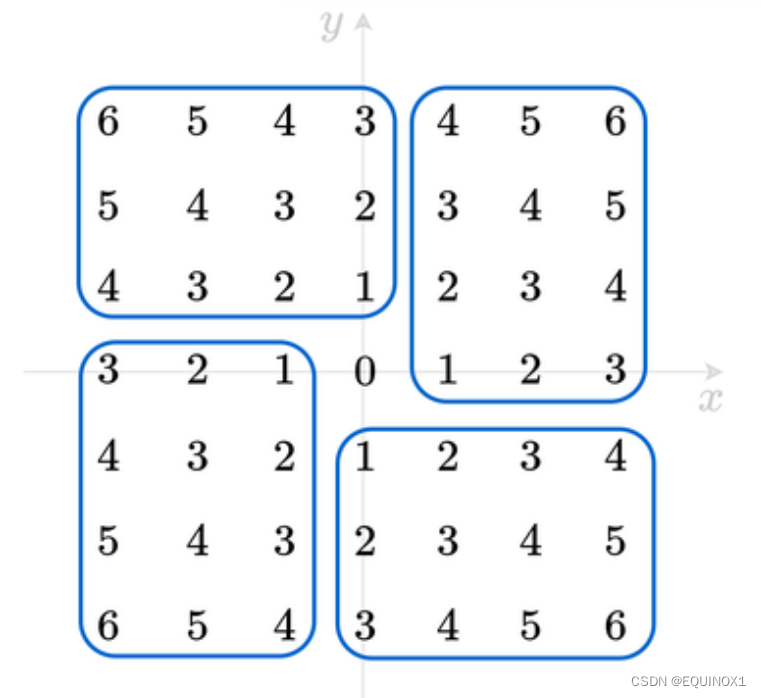
我们只需要计算出一个区域内的值然后乘4即可
我们设边长2n(由于以原点为中心,所以边长为偶数)
那么对于一个区域来说有n行n+1列
第一行为(n+1) * n / 2,每一行都比前一行多n,显然是首项为(n+1) * n / 2公差为n的等差数列
我们求得一个区域的总数然后乘4即可
sum = 4*n^3 + 6*n^2 + 2*n
2、复杂度
由于log(1000000)大概也就20上下,所以时间复杂度为O(1)
时间复杂度: O(1) 空间复杂度:O(1)
3、代码详解
class Solution {
public:long long minimumPerimeter(long long neededApples) {long long l = 1 , r = 1000000 , s = 0 , mid = 0;while(l < r){mid = (l + r) >> 1;s = (4*mid*mid*mid + 6*mid*mid + 2*mid);if(s >= neededApples) r = mid;else l = mid + 1;}return r << 3;}
};