人工智能_机器学习074_SVM支持向量机_软间隔与优化目标函数构建_C参数由来_惩罚误差点的惩罚度---人工智能工作笔记0114-编程知识

人工智能_机器学习074_SVM支持向量机_软间隔与优化目标函数构建_C参数由来_惩罚误差点的惩罚度---人工智能工作笔记0114

news/2025/2/3 7:04:38/文章来源:https://blog.csdn.net/lidew521/article/details/135209096

然后我们接着上一节再来看一下这里我们说有个

min_faces_per_person = 0 这个可以看到如果我们写上0,就意味着要加载所有的人脸图片,就会花费的时间久对吧

我们可以试试,这里我们 min_faces_per_person = 0 改成0然后

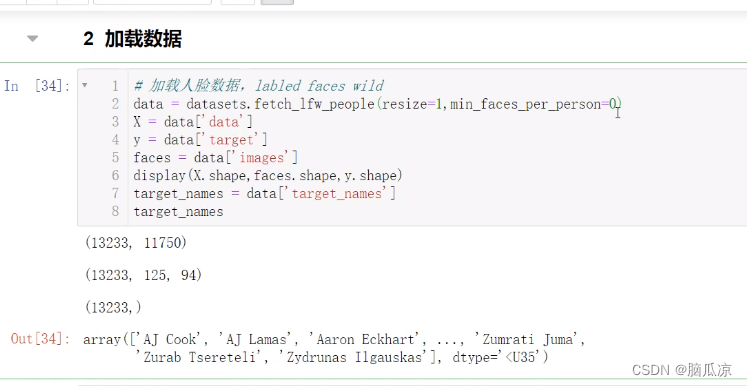
我们等一会加载完了以后,我们用

display(X.shape,faces.shape,y.shape)

显示一下,可以看到 13233 个人脸图片对吧,

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/299492.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

5g消息-5G时代短信升级-富媒体智能交互-互联网新入口

在5G时代，运营商和各大手机厂商都在积极推进5G消息的商用，基于短信入口的富媒体消息应用在近两年得到快速发展，并在企业端形成了广泛应用。作为5G时代的数字原生应用，5G消息支持用户通过文字、图片、音频、视频、位置等富媒体方式…

Windows操作系统中：共享文件夹以及防火墙介绍

目录一.共享文件夹 1.什么是共享文件夹 2.共享文件夹的优点以及不足优点不足之处 3.实际案例操作共享介绍普通共享实例展示高级共享实例展示二.防火墙 1.防火墙介绍主要功能 2.防火墙常见的应用场景 3.实例操作操作介绍出现的问题解决措施…

在Go语言中实现HTTP中间件

在Web开发中，中间件是一种非常流行的设计模式，它可以用于处理请求、拦截请求并对其进行处理或转换。而在Go语言中，实现HTTP中间件就像给自己的HTTP服务器穿上了一层“魔法外衣”，让它变得更加灵活、可配置和可扩展。下面&#xff…

椭球面系列---射线与椭球面的交点

射线与椭球体的交点问题的求解是一个非常常见和经典的问题，本文给出具体的计算原理和矩阵表达的过程，便于编程计算。见下图，已知射线(点为 p 0 \textbf{p}_0 p0，单位方向为 d \textbf{d} d)，那么与椭球面的交点 p …

android内存管理机制概览

关于作者：CSDN内容合伙人、技术专家， 从零开始做日活千万级APP。专注于分享各领域原创系列文章 ，擅长java后端、移动开发、人工智能等，希望大家多多支持。目录一、导读二、概览三、相关概念3.1 垃圾回收3.2 应用内存的分配与回…

50个免费的 AI 工具，提升工作效率（附网址）

上次我们已经介绍了20个精选的提高工作效率的免费AI工具，但如果你觉得这些AI工具还不过瘾的话，想进一步成为职场中最了解AI的人，本文将汇总介绍免费最新的50个AI工具。 DeepSwap DeepSwap 是一个基于 AI 的工具，适用于想要制作令人…

内存之-LeakCanary

关于作者：CSDN内容合伙人、技术专家， 从零开始做日活千万级APP。专注于分享各领域原创系列文章 ，擅长java后端、移动开发、人工智能等，希望大家多多支持。目录一、导读二、概览三、使用四、原理分析4.1 自动初始化4.1.1 初始化…

改善OEE的关键：从反应性维护向预测性维护转变

科技的进步正在对企业的日常运营模式产生影响。许多制造企业已经采用了自动化生产流程，这不仅提高了产品质量，还简化了设备维护流程，并使得制造企业的设备维护方式从反应性维护转变为预测性维护。人们发现，设备维护方式的转变显著…

前端通过不同方式画等腰梯形

1.css画说明：css画出倒梯形 <div class"outer-box"><div class"gradient_bg"></div></div> .outer-box{width: 50px;height: 50px;position: relative;//overflow: hidden; } /*使用transform属性后，梯形…

[kubernetes]Kube-APIServer

API Server API Server是什么提供集群管理的REST API接口，包括认证授权、数据校验以及集群状态变更等提供其他模块之间的数据交互和通信的枢纽（其他模块通过API Server查询或修改数据，只有API Server才直接操作etcd） 访问控制…

统计学常见概率分布

1.离散型随机变量 E ( X ) ∑ i 1 n x i p i E(X)\sum_{i1}^{n}x_ip_i E(X)i1∑nxipi D ( X ) σ 2 E ( X 2 ) − [ E ( X ) ] 2 D(X)\sigma^2E(X^2)-[E(X)]^2 D(X)σ2E(X2)−[E(X)]2 1.1 二项分布 n n n个相同试验；每次试验只有2个可能的结果&#xff1…

插入排序详解（C语言）

前言插入排序是一种简单直观的排序算法，在小规模数据排序或部分有序的情况下插入排序的表现十分良好，今天我将带大家学习插入排序的使用。let’s go ! ! ! 插入排序插入排序的基本思想是将待排序的序列分为已排序和未排序两部分。初始时&#xff0c…

人工智能_机器学习074_SVM支持向量机_软间隔与优化目标函数构建_C参数由来_惩罚误差点的惩罚度---人工智能工作笔记0114

相关文章