Python函数进阶与文件操作
一、作业回顾
1、格式化输出与%百分号
以下结果中,可以正常输出“50%及格”语句是(B)
A、print(“%d%及格” % (50)) => 回答大部分结果(Python这种写法不正确)
B、print(“%d%%及格” % (50)) => 正确结果
2、字符串切片
定义一个字符串str1 = ‘abcdefg’,使用切片截取字符串str1[3::-2],求返回结果:(C)
C、‘db’
3、字典的定义
其实字典中的key可以是很多数据类型(不可变数据类型 => 整型、浮点型、字符串、元组)
my_dict = {}
my_dict[1] = 1
my_dict['1'] = 2
my_dict[1.0] = 3
print(my_dict[1] + my_dict['1'] + my_dict[1.0])
二、引用变量与可变、非可变类型
1、引用变量
在大多数编程语言中,值的传递通常可以分为两种形式“值传递与引用传递”,但是在Python中变量的传递基本上都是引用传递。
☆ 聊聊变量在内存底层的存储形式
a = 10
第一步:首先在计算机内存中创建一个数值10(占用一块内存空间)
第二步:在栈空间中声明一个变量,如a
第三步:把数值10的内存地址赋予给变量小a,形成所谓的==“引用关系”==

☆ 如何验证Python中变量的引用关系
答:可以使用内置方法id(),其参数就是要显示的变量信息 => id(变量名称)
a = 10
print(id(a))
☆ 把一个变量赋予给另外一个变量的影响
a = 10
b = a
print(id(a))
print(id(b))
运行结果:

说明:由以上运行结果可知,当我们把一个变量赋予给另外一个变量时,其两者指向的内存地址相同。就说明a和b指向了同一块内存空间,原理图如下:
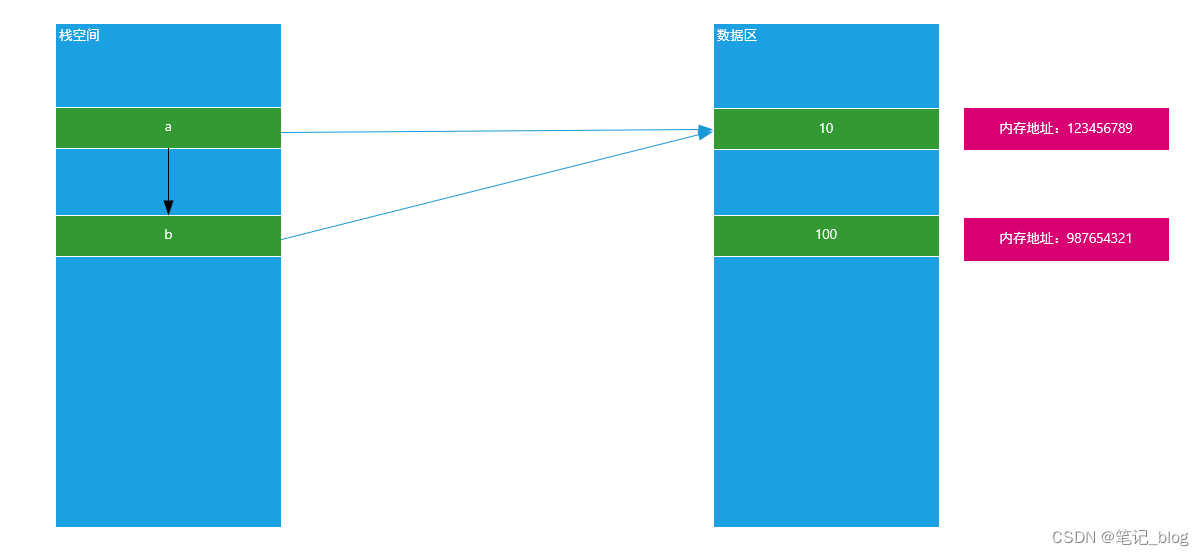
思考:如果在b = a以后,我们改变了变量a的值,问变量b是否会受到影响?
# a = 10
# print(id(a))a = 10
b = aa = 100
print(b) # 10 或 100print(id(a))
print(id(b))
原理图:

总结:不可变数据类型(数值)在赋值以后,其中一个值的改变不影响另外一个变量,因为两者指向空间地址不同。
2、Python中可变和非可变数据类型
☆ 问题1:在Python中一共有几种数据类型?
答:7种,数值(int整型、float浮点类型)、bool类型(True和False)、字符串类型(str)、元组(tuple 1,2,3)、列表(list [1, 2, 3])、字典(dict {key:value})、集合(set {1, 2})
在Python中,我们可以把7种数据类型分为两大类:可变类型 + 非可变类型
① 非可变类型
数值(int整型、float浮点类型)
bool类型(True和False)
字符串类型(str)
元组(tuple 1,2,3)
② 可变类型
列表(list [1, 2, 3])
字典(dict {key:value})
集合(set {1, 2})
☆ 问题2:如何判断一个数据类型是可变类型还是非可变类型?
在Python中,可变类型与非可变类型主要是通过这个数据类型在内存中的表现形式来进行定义的。
① 可变类型就是在内存中,其内存地址一旦固定,其值是可以发生改变的
a = [1, 2, 3]
print(id(a))# 向内存中追加新数据(对数据进行改变只能通过数据类型.方法()实现)
a.append(4)
print(id(a))
原理图:
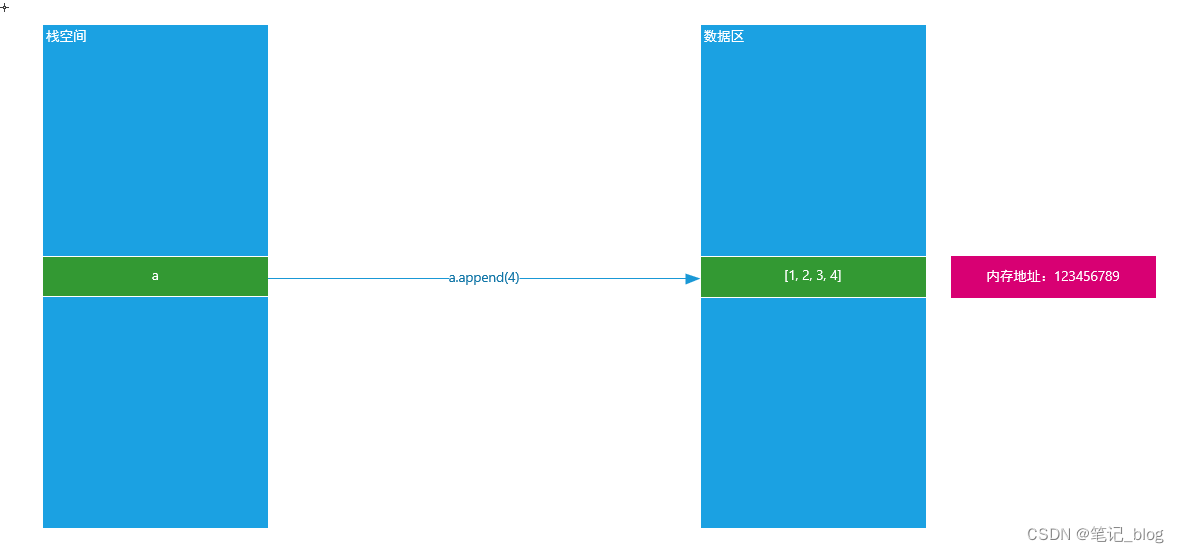
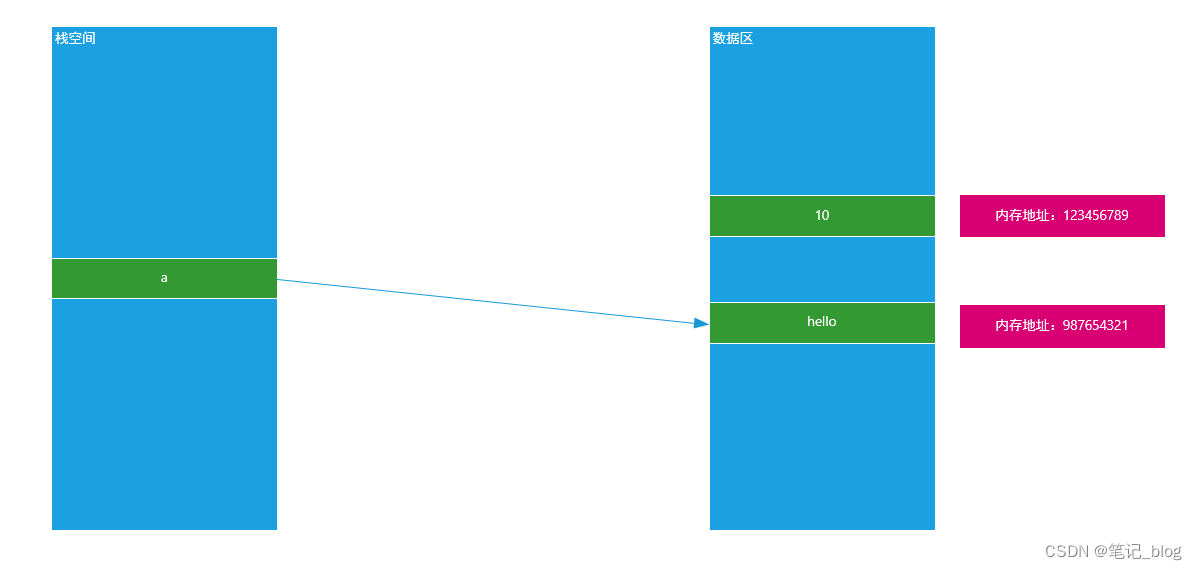
② 非可变类型就是在内存中,内存地址一旦固定,其值就没办法发生任何改变了
a = 10
print(id(a))a = 'hello'
print(id(a))
原理图:
3、可变类型与非可变类型在函数中的应用
☆ 可变类型
# 定义一个函数
def func(names):print(names)# 定义一个全局变量
names = ['张三', '李四', '王五']
# 调用函数
func(names)
原理图:
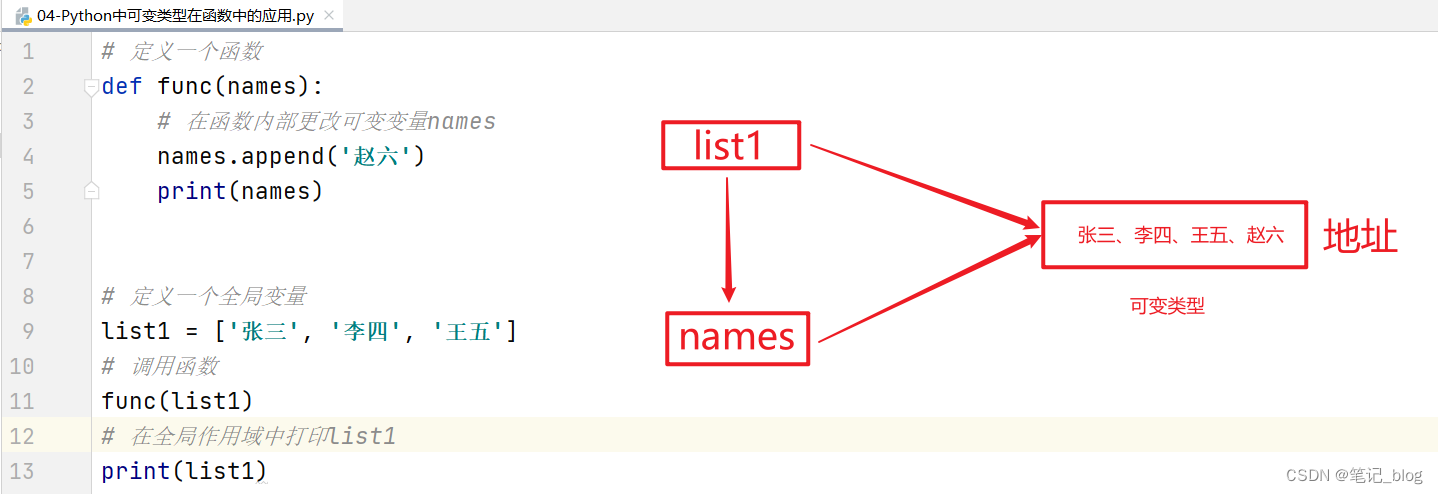
综上所述:可变类型在函数中,如果在全局或局部中对可变类型进行增删改操作,其外部和内部都会受到影响。
☆ 不可变类型
# 定义一个函数
def func(num):num += 1print(num)# 定义一个全局变量
a = 10
# 调用函数
func(a)
# 在全局作用域中打印a
print(a)
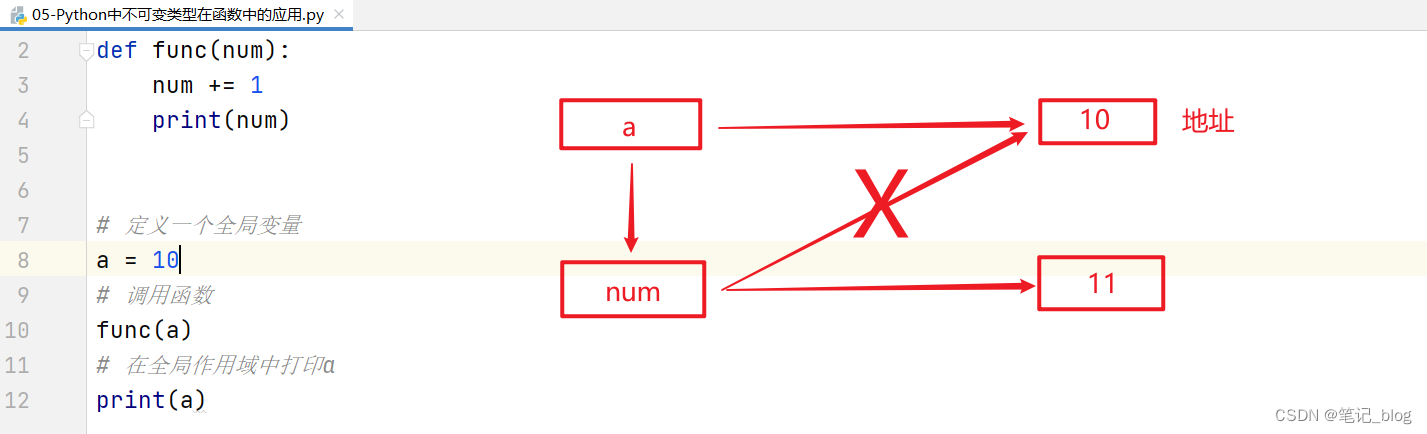
综上所述:不可变类型在函数中,局部或全局的改变对外部和内部都没有任何影响。
三、函数递归(重点难点)
1、前言
编程思想:如何利用数学模型,来解决对应的需求问题;然后利用代码实现对应的数据模
算法:使用代码实现对应的数学模型,从而解决对应的业务问题
程序 = 算法 + 数据结构
在我们经常使用的算法中,有两种非常常用的算法:递推算法 + 递归算法,专门用于解决一些比较复杂,但是拆分后相似度又非常高的程序。
2、递推算法
递归算法:递推算法是一种简单的算法,即通过已知条件,利用特定条件得出中间推论,直至得到结果的算法。递推又分为顺推和逆推。
顺推:通过最简单的条件,然后逐步推演结果
逆推:通过结果找到规律,然后推导已知条件
递推算法案例:斐波那契数列
1 1 2 3 5 8 13 21 …
① ② ③ ④ ⑤ ⑥ …
第1位为1,第2位为1,第3位为2 = 1 + 1,第4位为3 = 2 + 1,依次类推…第n位结果为多少?
f(n) = f(n-1) + f(n-2)
提出问题:求斐波那契数列第15位的结果?
分析:f(15) = f(14) + f(13)
f(14) = f(13) + f(12)
f(13) = f(12) + f(11)
…
f(4) = f(3) + f(2) = 3 + 1
f(3) = f(2) + f(1) = 2
f(2) = 1
f(1) = 1
递推算法:使用while循环或for循环
# 递推算法:根据已知条件,求结果(或者根据结果求未知条件)
def recusive(n):""" 返回斐波那契数列某一位(n>=1)的结果 """if n == 1 or n == 2:return 1