C++:stack、queue、priority_queue增删查改模拟实现
- 前言
- 一、C++stack的介绍和使用
- 1.1 引言
- 1.2 satck模拟实现
- 二、C++queue的介绍和使用
- 2.1 引言
- 2.2 queue增删查改模拟实现
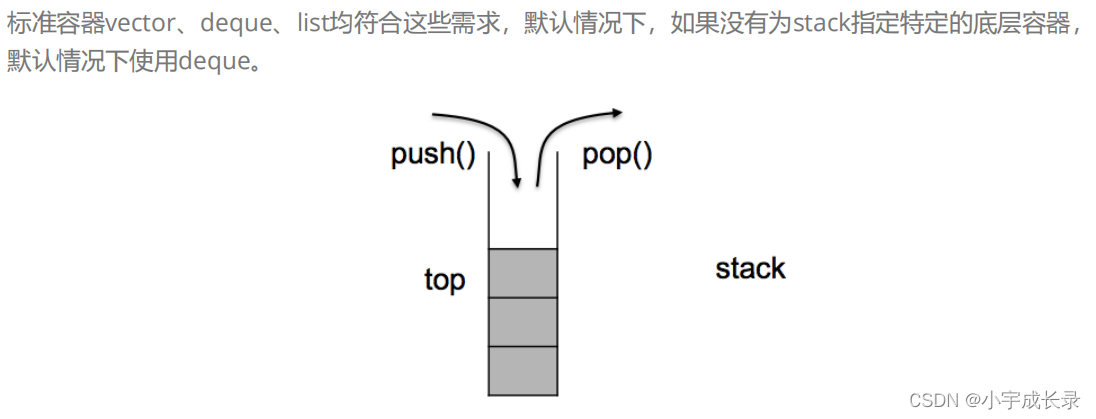
- 三、STL标准库中stack和queue的底层结构:deque
- 3.1 deque的简单介绍(了解)
- 3.2 deque的缺陷
- 3.3 为什么选择deque作为stack和queue的底层默认容器
- 四、priority_queue的介绍和实现
- 4.1 priority_queue的介绍
- 4.1 priority_queue的介绍增删查改模拟实现
- 前言
- 4.1.1 push()
- 4.1.2 pop()
- 4.3 top()、size()、empty()
- 4.1 priority_queue(优先级队列)增删查改模拟实现
- 五、所有代码
前言
一、C++stack的介绍和使用
1.1 引言
我们先来看看
stack的相关接口有哪些:

从栈的接口,我们可以知道栈的接口是一种特殊的vector,所以我们完全可以使用vector来模拟实现stack。
1.2 satck模拟实现
因此我们可以将底层容器定义成模板,然后将容器类变量作为成员变量进行封装。在实现satck的各种接口时,通过成员变量来调用底层容器的接口。(这就是容器适配器,将容器作为底层复用)
namespace achieveStack
{//对特定类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素,template<class T, class Container = deque<T>>//底层容器可以是: vector、list、deque(后续会说明)class stack{public:void push(const T& x){//调用容器_con的尾插_con.push_back(x);}void pop(){//调用容器_con的头删_con.pop_back();}const T& top(){//调用容器_con的接口backreturn _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};
}
二、C++queue的介绍和使用
2.1 引言
同样,我们下来看看queue的接口究竟有哪些:

2.2 queue增删查改模拟实现
因为queue的接口中存在头删和尾插,因此使用vector来封装效率太低,故可以借助list来模拟实现queue。和stack一样,queue默认底层容器为deque(后续会介绍),此外还可以用list。
具体如下:

namespace achieveQueue
{template<class T, class Container = deque<T>>class queue{public:void push(const T& x)//尾插{_con.push_back(x);}void pop()//头删{_con.pop_front();}const T& front()//首元素{return _con.front();}const T& back()//尾元素{return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Container _con;};
}
三、STL标准库中stack和queue的底层结构:deque
虽然stack和queue中也可以存放元素,但在STL中并没有将其划分在容器的行列,而是将其称为容器适配
器,这是因为stack和队列只是对其他容器的接口进行了包装,STL中stack和queue默认使用deque,比如:

3.1 deque的简单介绍(了解)
deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比较高。
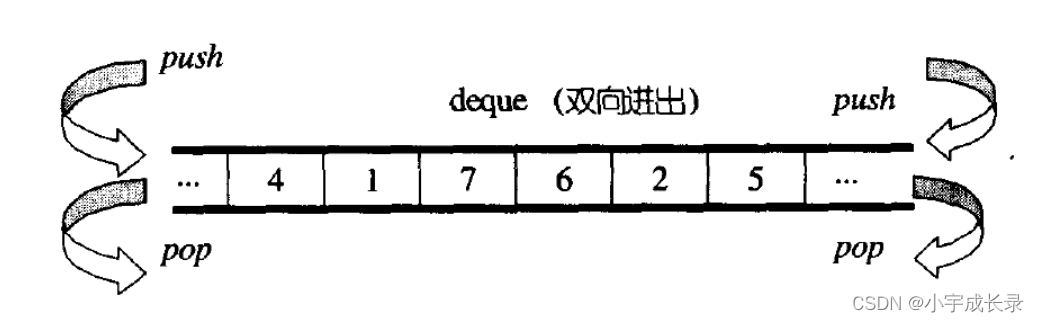
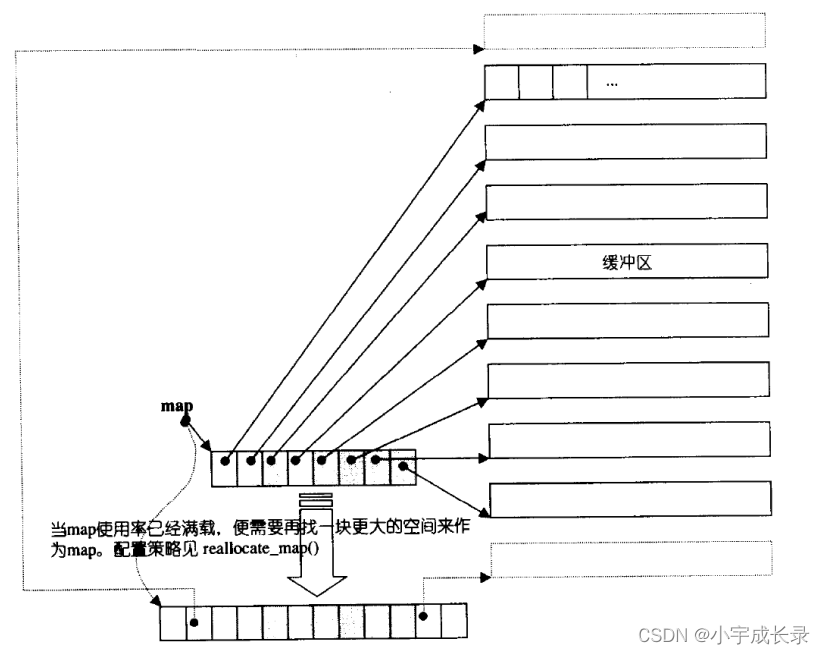
deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际deque类似于一个动态的二维数组,其底层结构如下图所示:
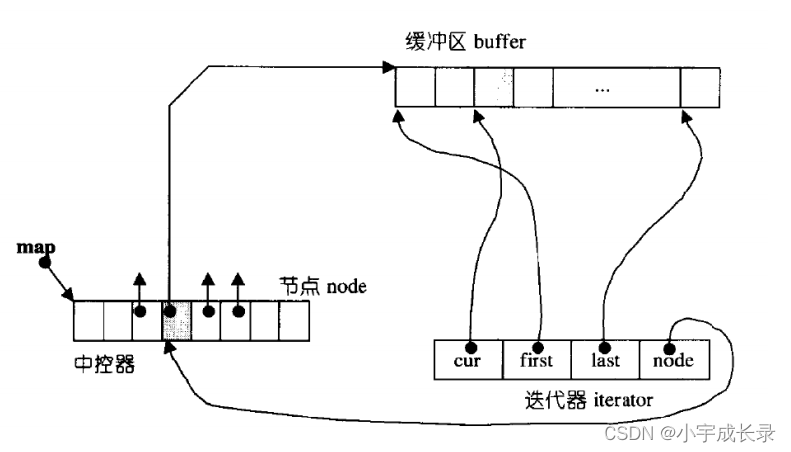
双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问的假象,落在了deque的迭代器身上,因此deque的迭代器设计就比较复杂,如下图所示:
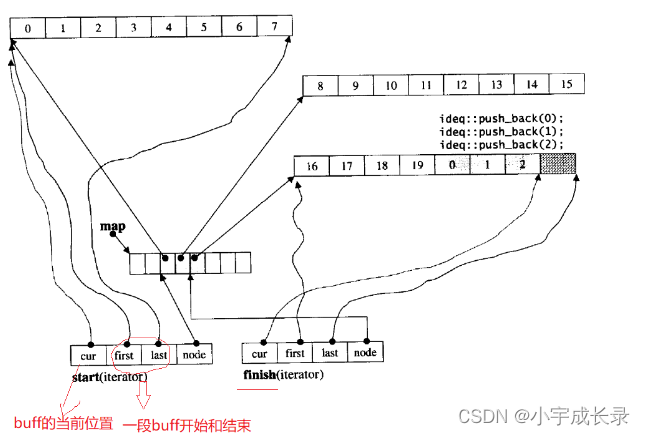
那deque是如何借助其迭代器维护其假想连续的结构呢?具体如下:
3.2 deque的缺陷
与vector比较,deque的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不需要搬移大量的元素,因此其效率是必vector高的。
与list比较,其底层是连续空间,空间利用率比较高,不需要存储额外字段。
但是,deque有一个致命缺陷:不适合遍历,因为在遍历时,deque的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构时,大多数情况下优先考虑vector和list,deque的应用并不多,而目前能看到的一个应用就是,STL用其作为stack和queue的底层数据结构。
3.3 为什么选择deque作为stack和queue的底层默认容器
stack是一种后进先出的特殊线性数据结构,因此只要具有push_back()和pop_back()操作的线性结构,都可
以作为stack的底层容器,比如vector和list都可以;queue是先进先出的特殊线性数据结构,只要具有
push_back和pop_front操作的线性结构,都可以作为queue的底层容器,比如list。但是STL中对stack和
queue默认选择deque作为其底层容器,主要是因为:
- stack和queue不需要遍历(因此stack和queue没有迭代器),只需要在固定的一端或者两端进行操作。
- 在stack中元素增长时,deque比vector的效率高(扩容时不需要搬移大量数据);queue中的元素增长
时,deque不仅效率高,而且内存使用率高。
结合了deque的优点,而完美的避开了其缺陷。
四、priority_queue的介绍和实现
4.1 priority_queue的介绍
和前面一样,我们先来看看priority_queue的接口。
priority_queue(优先级队列)默认使用vector作为其底层存储数据的容器,在vector上又使用了堆算法将vector中元素构造成堆的结构,因此priority_queue就是堆,所有需要用到堆的位置,都可以考虑使用priority_queue。注意:默认情况下priority_queue是大堆(如需修改为小堆,可以将传入的默认仿函数less改为greater)。

4.1 priority_queue的介绍增删查改模拟实现
接下来如向下调整、向上调整等都是堆的知识,不懂的参考:【数据结构入门指南】二叉树顺序结构: 堆及实现(全程配图,非常经典)
前言
由于优先队列是一种容器适配器,所以我们可以使用模板将容器作为其成员变量,根据实际传入的容器生成实例化出具体版本。同时我们不仅要实现小堆还有大队,所以我们可以增加一个比较函数的模板参数,根据传入的函数来决定是大队还是小堆。
大致如下:
namespace achievePriority_queue//命名空间
{template<class T, class Container=vector<T>,class Compare = less<T>>class priority_queue{public:priority_queue()//默认构造{}private:Compare com;Container _con;};
}
4.1.1 push()
【分析】:我们可以先尾插数据,由于priority_queue的数据是一个堆结构,还需要将数据调整到合适位置。而插入的数据影响的只是当前元素到祖先之间父子节点关系,所以我们可以采用向上调整算法。
【例子】:
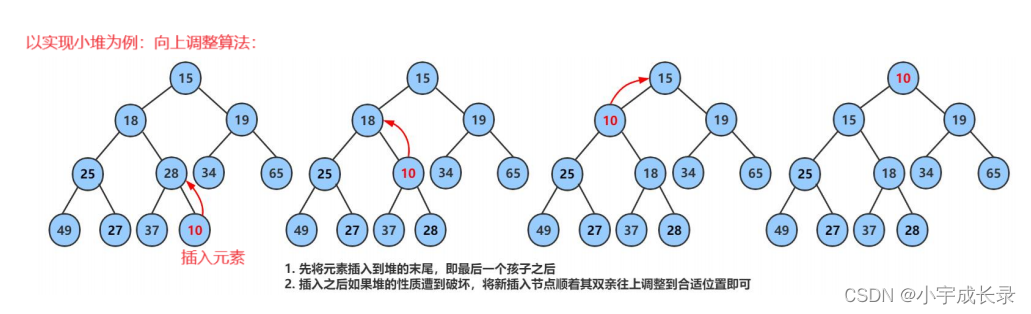
【代码如下】:
//向上调整
void adjust_up(int child)
{int parent = (child - 1) / 2;while (child > 0){if (com(_con[parent], _con[child])){swap(_con[parent], _con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}void push(const T& x)
{_con.push_back(x);//调用_con对于容器尾插接口adjust_up(_con.size() - 1);//向上调整
}4.1.2 pop()
【分析】:删除元素,即删除堆顶元素。我们可以先将堆顶元素和堆尾元素交换,在将堆尾元素删除(这样可以防止大量挪动数据)。但交换后的元素还需要调整到合适位置,即采用向下调整算法。
【例子】:
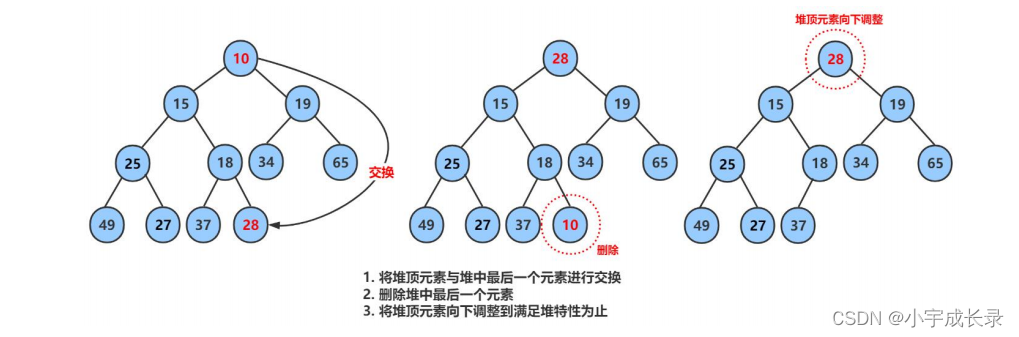
【代码如下】:
void adjust_down(int parent)//向下调整算法
{int child = 2 * parent + 1;while (child < _con.size()){if (child + 1 < _con.size() && com(_con[child], _con[child + 1])){child++;}if (com(_con[parent], _con[child])){swap(_con[parent], _con[child]);parent = child;child = 2 * parent + 1;}else{break;}}
}void pop()
{swap(_con[0], _con[_con.size() - 1]);//堆顶和堆尾元素交换_con.pop_back();//调用_con对于容器的尾删接口adjust_down(0);//向下调整算法
}
4.3 top()、size()、empty()
这些接口比较简单就不一一介绍了,具体代码如下:
const T& top()
{return _con[0];}size_t size(){return _con.size();}bool empty(){return _con.empty();}
4.1 priority_queue(优先级队列)增删查改模拟实现
五、所有代码
gitee:C++:stack、queue、priority_queue增删查改模拟实现