特征维度约减

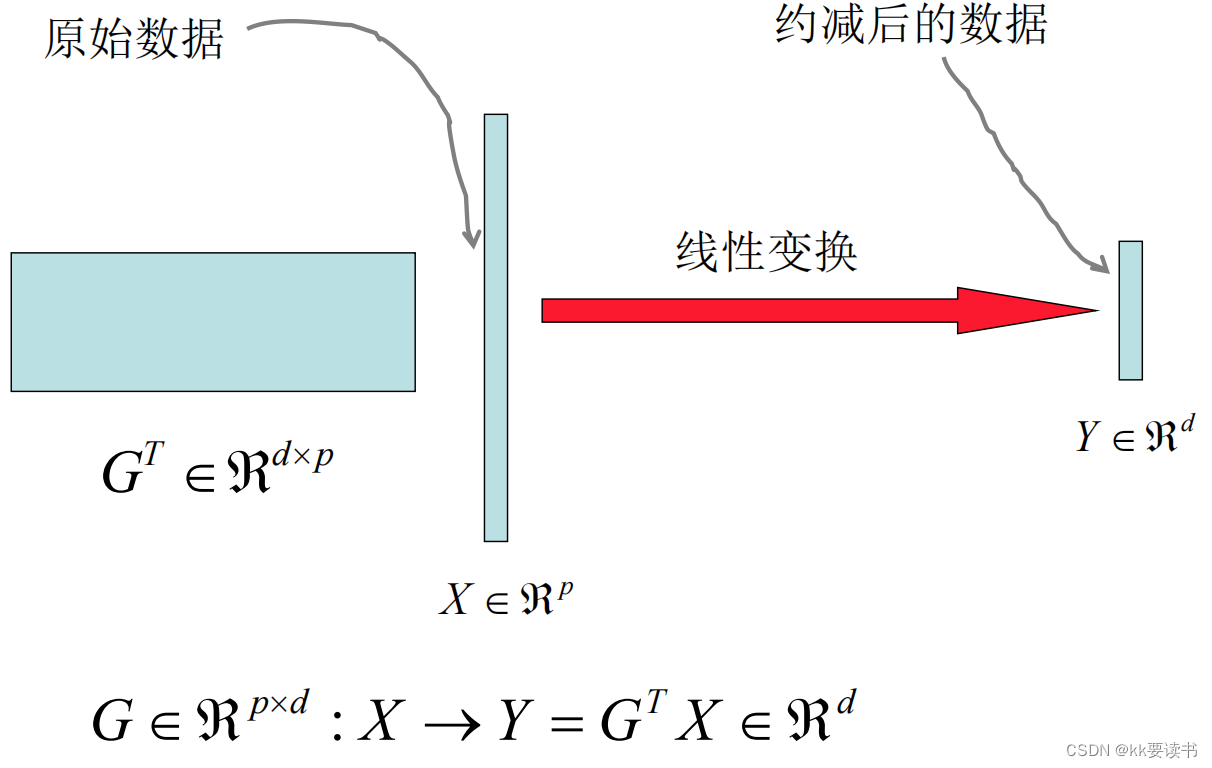
高维数据
为何要维度约减?
-
数据压缩和存储:高维数据通常需要占用更大的存储空间。通过维度约减,可以将数据压缩为较低维度的表示形式,减少存储需求。
-
降低计算复杂度:在高维空间中进行计算通常更加复杂和耗时。通过维度约减,可以将计算转移到低维空间中进行,从而降低计算复杂度和提高计算效率。
-
特征选择和提取:维度约减可以帮助我们识别和选择最重要的特征,去除冗余和噪声。这有助于提高模型的泛化能力和性能,并减少过拟合的风险。
-
可视化和解释:将高维数据映射到二维或三维空间,可以更容易地进行可视化和解释。我们可以观察数据在低维空间中的分布、结构和聚类情况,发现数据中的潜在模式和规律。
-
数据处理和挖掘:在高维空间中,数据点之间的距离和相似度更难确定。通过维度约减,可以使得数据点之间的距离和相似度更加明确和可靠,从而更好地进行数据处理和挖掘任务。
常规维度约减方法
-
监督学习:监督学习是指在有标注数据的前提下,通过构建模型来预测新的未知数据的标签或数值。监督学习需要使用一些已经标记好了标签的数据作为训练集,在模型训练过程中,计算模型预测值和实际值之间的误差,并不断调整模型参数使其错误率最小化。常见的监督学习算法包括决策树、支持向量机、神经网络等。
-
无监督学习:无监督学习是指在没有标注数据的情况下,尝试发现数据中的潜在模式和结构。无监督学习不需要已知的标签信息,而是将数据分成几个组或类,以便在后续的处理中可以更好地理解和处理数据。常见的无监督学习算法包括聚类、降维、异常检测等。
-
半监督学习:半监督学习是介于监督学习和无监督学习之间的学习方式。半监督学习旨在同时利用有标注和无标注数据来训练模型,以提高模型的性能。半监督学习算法通常利用少量的已标注数据来指导模型训练,同时结合大量未标注数据的信息进行模型优化。半监督学习经常用于在数据集标注成本较高、而未标注数据却很容易获取时。
主成分分析(PCA)
代数定义
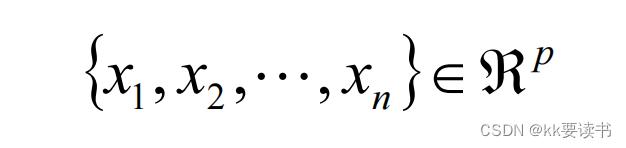
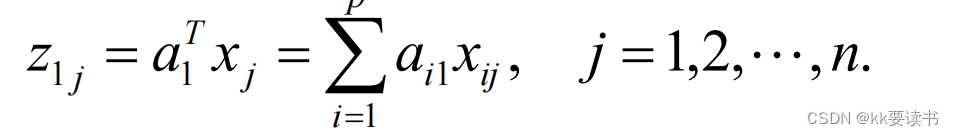
PCA算法流程
-
数据预处理:对原始数据进行标准化处理,使得数据各维度具有相同的重要性。
-
计算协方差矩阵:计算数据的协方差矩阵,该矩阵反映了数据之间的线性相关性。协方差矩阵的对角线元素为各个特征的方差,非对角线元素为特征之间的协方差。
-
计算特征值和特征向量:对协方差矩阵进行特征值分解,得到特征值和特征向量。其中,特征向量表示的是数据在新的坐标系下的主要方向,而特征值则代表了数据在该方向上的方差大小。
-
排序和选择主成分:将特征值从大到小排序,选择前k个特征值对应的特征向量作为新的坐标系的主要方向。
-
构造新的特征空间:将原始数据投影到新的坐标系中,得到降维后的数据集。


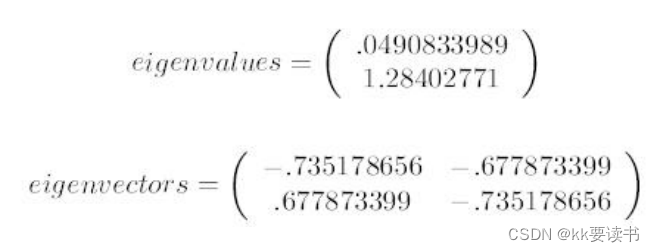

代码实现
下面使用svm和pca实现,对人脸图片进行PCA降维,并用SVM进行分类。
# 导入相关模块
from __future__ import print_function
from time import time
import logging
import cv2
import matplotlib.pyplot as plt
from numpy import *
import numpy as np
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.metrics import ConfusionMatrixDisplay
from sklearn.decomposition import PCA
from sklearn.svm import SVC
import zipfile
import os
from sklearn.utils.fixes import loguniform
from sklearn.model_selection import RandomizedSearchCV数据预处理
# 解压数据集,请学习zipfile的用法
import zipfile
extracting = zipfile.ZipFile('./data/data76601/crop_images.zip')
extracting.extractall('./data/crop_images')# 画图函数
def plot_gallery(images, titles, h, w, n_row=4, n_col=4): # n_row=4, n_col=4表示一行有几张图,一列有几张图"""Helper function to plot a gallery of portraits"""plt.figure(figsize=(2.1 * n_col, 2.8 * n_row)) # 确定了图片的尺寸plt.subplots_adjust(bottom=0, left=.01, right=.99, top=.90, wspace=.75, hspace=.35)for i in range(n_row * n_col):plt.subplot(n_row, n_col, i + 1) # n_row行,n_col列,位置是第i+1个,从1开始 # cmap: 颜色图谱(colormap), 默认绘制为RGB(A)颜色空间plt.imshow(images[i].reshape((h, w)), cmap=plt.cm.gray) # 画图plt.title(titles[i], size=12)plt.xticks(())plt.yticks(())#获得数据集中的七个人名和数字组成的字典+得到所有照片的地址
def get_name(file_dir):"""用来得到数据集中的七个人名和数字组成的字典+得到所有照片的二维列表地址:param file_dir:新数据的名字:return:返回一个字典+一个二维列表"""all_dirs = []all_path = []count = 0for root, dirs, files in os.walk(file_dir): # 分别从文件地址中,读出根地址、子目录、文件名all_dirs.append(dirs) # 子目录就是这个人的名字,所以要存下来temp = []if count == 0:count += 1continuefor file in files:temp.append(os.path.join(root, file)) # 这里每次循环存的就是一个人70张照片地址count += 1all_path.append(temp) # 得到7*70的照片地址,二维的all_dirs = all_dirs[0] # 得到一维的人脸照片名number = [i for i in range(7)]name_dict = dict(zip(number, all_dirs)) # 得到人名字典return name_dict, all_path # 返回的分别是名字字典7、二维7*70图片地址# 获取名字字典+所有图片的二维地址
name_dict = {}
all_path = []
file_new_path = r'./data/crop_images'
name_dict, all_path = get_name(file_new_path)
print(name_dict)
print(np.shape(all_path))# 读取数据
all_data_set = []
all_data_label = []
def get_Image():for i in range(7):for j in range(50):images_path = all_path[i][j]img = cv2.imread(images_path)img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 改为灰度图,颜色空间转换函数h, w = img_gray.shapeimg_col = img_gray.reshape(h * w)all_data_set.append(img_col) # 存图片all_data_label.append(i) # label#返回图片大小return h, w
#获得图片大小
h, w = get_Image()#整理数据
# 将列表改成数组
X = array(all_data_set)
y = array(all_data_label)n_samples, n_features = X.shape
n_classes = len(unique(y))target_names = []
for i in range(7):names = name_dict[i]target_names.append(names) # 用图片文件名中的人名print("n_samples: %d" % n_samples) # 图片总量
print("n_features: %d" % n_features) # 每张图片内按尺寸定的数量,行列尺寸相乘
print("n_classes: %d" % n_classes) # 标签总量数据集划分
# 划分数据
#要求:1、3/4用于训练,1/4用于测试;2、random_state设为1,随机种子保证得到相同随机数,保证每次运行结果一致。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42)PCA提取特征(降维)
# 这个部分是提取特征脸的过程,本来想分开,但是为了保持整体性我又把他们放在一起了,我会尽量做注释n_components = 95 # 定义取的特征脸数量,经过测试:95准确率相对高
print("Extracting the top %d eigenfaces from %d faces" % (n_components, X_train.shape[0]))
t0 = time()
# 选择一种svd方式,whiten是一种数据预处理方式,会损失一些数据信息,但可获得更好的预测结果
pca = PCA(n_components=n_components, svd_solver='full', whiten=True).fit(X_train) # 经过测试,full最好
print("done in %0.3fs" % (time() - t0))eigenfaces = pca.components_.reshape((n_components, h, w)) # 特征脸print("Projecting the input data on the eigenfaces orthonormal basis")t0 = time()
X_train_pca = pca.transform(X_train) # 得到训练集投影系数
X_test_pca = pca.transform(X_test) # 得到测试集投影系数
# 接下来我们就会使用投影系数来进行训练
print("done in %0.3fs" % (time() - t0))# 最后我们得到了特征脸,画个图看看把
# plot the gallery of the most significative eigenfaces画出最有意义的面孔
eigenface_titles = ["eigenface %d" % i for i in range(eigenfaces.shape[0])]
plot_gallery(eigenfaces, eigenface_titles, h, w)plt.show()SVM分类器
这个部分就是进行训练了,采用的是SVM,最终得到不错的SVM分类器print("Fitting the classifier to the training set") # 将分类器拟合到训练集
t0 = time()
'''C为惩罚因子,越大模型对训练数据拟合程度越高,gama是高斯核参数'''
param_grid = {'C': [5e2, 1e3, 5e3, 1e4, 5e4, 1e5],'gamma': [0.0001, 0.0005, 0.001, 0.002, 0.0009, 0.005, 0.01, 0.1], }# 我在这里要选取一系列可能是最优的超参数C和gamma,然后在下面中找到最优的
# 分类器是SVC组成的这个高斯核(RBF)+balanced防止过拟合
clf = GridSearchCV(SVC(kernel='rbf', class_weight='balanced'), param_grid) # 超参数自动搜索模块,按你的要求,在你给定的超参数范围内选一个最合适的
# 表示调整各类别权重,权重与该类中样本数成反比,防止模型过于拟合某个样本数量过大的类clf = clf.fit(X_train_pca, y_train)
print("done in %0.3fs" % (time() - t0))
print("Best estimator found by grid search:") # 用网格搜索找到最佳估计量
print(clf.best_estimator_) # 让我们看一下都有哪些分类器弄好了的超参数用训练好的SVM分类器预测
# 下面用训练好的分类器进行预测print("Predicting people's names on the test set") # 在测试集中预测人们的名字
t0 = time()
y_pred = clf.predict(X_test_pca) # 进行预测
#y_pred = clf.predict(X_test) # 进行预测print("done in %0.3fs" % (time() - t0))print(classification_report(y_test, y_pred, target_names=target_names)) # 查准率/查全率/F1值/测试样本数
#print(confusion_matrix(y_test, y_pred, labels=range(n_classes)))# plot the result of the prediction on a portion of the test set
# 在测试集的一部分上绘制预测结果def title(y_pred, y_test, target_names, i):pred_name = target_names[y_pred[i] - 1]true_name = target_names[y_test[i] - 1]return ' predicted: %s\n true: %s' % (pred_name, true_name)# 画图展示
prediction_titles = [title(y_pred, y_test, target_names, i) for i in range(y_pred.shape[0])]
plot_gallery(X_test, prediction_titles, h, w)plt.show()总结
主成分分析(Principal Component Analysis,PCA)是一种常用的降维方法和数据分析技术。它可以将高维数据映射到低维空间,并保留最重要的特征信息。
PCA的核心思想是通过线性变换将原始数据映射到新的坐标系下,使得在新的坐标系中,数据的方差最大化。具体步骤如下:
-
标准化数据:将原始数据进行标准化处理,使得所有特征具有相同的尺度,避免某些特征对结果的影响过大。
-
计算协方差矩阵:计算标准化后的数据的协方差矩阵。协方差矩阵描述了数据之间的相关性。
-
计算特征值和特征向量:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。特征值表示了新坐标系下的方差,特征向量则定义了新坐标系的方向。
-
选择主成分:根据特征值的大小,选择最大的K个特征值对应的特征向量作为主成分。
-
数据映射:将原始数据投影到选择的主成分上,得到降维后的数据。
PCA的应用包括数据降维、数据可视化、特征提取等。通过降低数据的维度,PCA可以减少计算复杂度、消除冗余信息、去除噪声、提高模型性能等。同时,PCA还可以帮助我们理解数据之间的关系和结构,发现数据中的潜在模式和规律。