前言:本题是一道逻辑细节题,考察阅读理解并转化为代码的能力,很多细节
题目描述:
你正在经营一座摩天轮,该摩天轮共有 4 个座舱 ,每个座舱 最多可以容纳 4 位游客 。你可以 逆时针 轮转座舱,但每次轮转都需要支付一定的运行成本 runningCost 。摩天轮每次轮转都恰好转动 1 / 4 周。
给你一个长度为 n 的数组 customers , customers[i] 是在第 i 次轮转(下标从 0 开始)之前到达的新游客的数量。这也意味着你必须在新游客到来前轮转 i 次。每位游客在登上离地面最近的座舱前都会支付登舱成本 boardingCost ,一旦该座舱再次抵达地面,他们就会离开座舱结束游玩。
你可以随时停下摩天轮,即便是 在服务所有游客之前 。如果你决定停止运营摩天轮,为了保证所有游客安全着陆,将免费进行所有后续轮转 。注意,如果有超过 4 位游客在等摩天轮,那么只有 4 位游客可以登上摩天轮,其余的需要等待 下一次轮转 。
返回最大化利润所需执行的 最小轮转次数 。 如果不存在利润为正的方案,则返回 -1 。
示例 1:
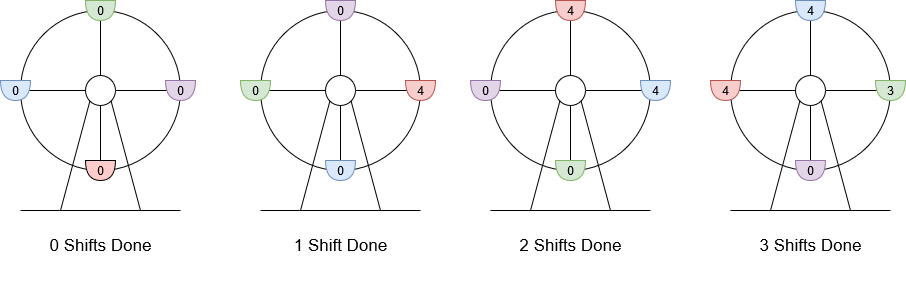
输入:customers = [8,3], boardingCost = 5, runningCost = 6 输出:3 解释:座舱上标注的数字是该座舱的当前游客数。 1. 8 位游客抵达,4 位登舱,4 位等待下一舱,摩天轮轮转。当前利润为 4 * $5 - 1 * $6 = $14 。 2. 3 位游客抵达,4 位在等待的游客登舱,其他 3 位等待,摩天轮轮转。当前利润为 8 * $5 - 2 * $6 = $28 。 3. 最后 3 位游客登舱,摩天轮轮转。当前利润为 11 * $5 - 3 * $6 = $37 。 轮转 3 次得到最大利润,最大利润为 $37 。
大体思路:每走一轮计算一次利润,并更新最大利润值,直到把没人等待。
代码实现:
class Solution {
public:int minOperationsMaxProfit(vector<int>& customers, int boardingCost, int runningCost) {int total_q=0;//计算利润时总共上去摩天轮的人数int curq=0;//目前等待的人int profit=0;//利润int maxprofit=-INT_MAX;//最大利润int times=0,max_times=0;//次数,最大利润出现的次数int i;//先进行for循环把cuostomers全取出来for( i=0;i<customers.size();i++){curq+=customers[i];if(curq>4){total_q+=4;curq-=4;profit=total_q*boardingCost-runningCost*(i+1);}else{total_q+=curq;curq=0;profit=total_q*boardingCost-runningCost*(i+1);}//每次进行比较,如果当前利润最大,就取最大利润所在的次数,记得i+1maxprofit=max(maxprofit,profit);if(maxprofit==profit)max_times=i+1;}times+=i;//前面i次搞完后把剩下的customers再送上去,同样的逻辑while(curq){if(curq>4){total_q+=4;curq-=4;profit=total_q*boardingCost-runningCost*(++i);}else{total_q+=curq;curq=0;profit=total_q*boardingCost-runningCost*(++i);}times++;//这里如果相等则取次数小的一次if(maxprofit<profit){max_times=times;maxprofit=profit;}}if(maxprofit<=0)return -1;return max_times;}
};

![[每周一更]-(第46期):Linux下配置Java所需环境及Java架构选型](https://img-blog.csdnimg.cn/direct/6147f39dab1041618e8ccf5afef33aea.png#pic_center)