交通 | 司乘匹配：基于增量成本计算的优化算法-编程知识

在这里插入图片描述

编者按：

司乘匹配是打车服务中一项至关重要的任务，如果这一步做得不够优化，可能导致乘客需要更长的时间才能到达目的地，同时司机的收入也会因此减少。由于司乘匹配是一个持续进行的过程，每一时刻都在不断涌入新的打车订单和新的司机，这使得计算最优匹配成为一项非常具挑战性的任务。今天解读的这篇文章是由东南亚打车公司Grab在2021年发表于数据库顶会VLDB [1]，并被评选为当年的Best Scalable Data Science Paper。作者发现了一个有意思的事情，最优匹配问题中最常用的Kuhn-Munkres算法（也称为匈牙利算法）中的一步对算法的效率提升有很大的影响，并且作者还用实际场景中观察到的一个特性来改进算法，今天我们将结合作者自己曾经写过的技术博客 [2]，来从一个全新的角度探讨司乘匹配问题。
[1] Tenindra Abeywickrama, Victor Liang, and Kian-Lee Tan. 2021. Optimizing bipartite matching in real-world applications by incremental cost computation. Proc. VLDB Endow. 14, 7 (March 2021), 1150–1158
[2] https://engineering.grab.com/using-real-world-patterns-to-improve-matching

一、引例

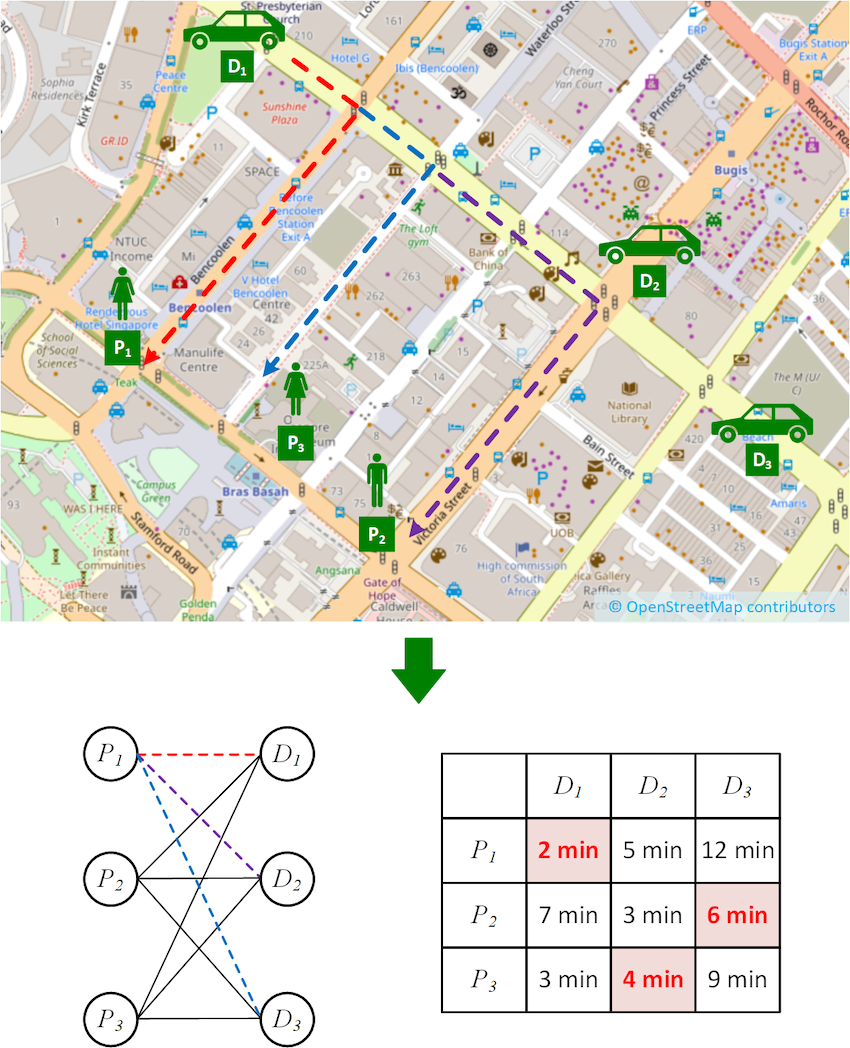
在这里插入图片描述
图1. 司乘匹配场景示例

让我们从图1所示的简单匹配场景开始来介绍一些基础的概念，假设有三位司机（D1、D2 和 D3）和三位乘客（P1、P2 和 P3），乘客和司机是通过行驶时间来进行匹配的，找到行驶时间涉及计算从每位司机到每位乘客的最快路径，例如从 D1 到 P1、P2 和 P3 的虚线路径。为了找到最小总行驶时间的司乘分配方案，我们可以把问题表示为下面显示的二分图。在二分图中，乘客集合和司机集合分别构成二分图的两个集合，连接它们的边代表着最短路径，相对应的行驶时间如右侧矩阵所示，这个矩阵我们称它为成本矩阵。寻找两个集合间的最优分配也被称为解决最小权重二分匹配问题（也称为分配问题），一种常用来解决这个问题的算法叫Kuhn-Munkres（KM）算法（也称为匈牙利算法）。回忆一下，KM算法的原理是在不断迭代更新二分集合 𝑈（相应地，𝑉）的一组标签 $l_u$ （或 $l_v$ ），以生成降低的成本 $c_r(u,v)=c(u,v)-l_u-l_v$ 为零的边。如果在这些边之间存在完美匹配，那么这个匹配就是最小权重二分匹配问题的最优解。用KM算法来求解以上示例，我们会得到成本矩阵上标红的最优匹配方案，即 $P_1 -D_1, P_2 -D_3, P_3 -D_2$ 。然而到目前为止，我们都还没有涉及到和成本矩阵计算相关的事情，而事实证明，在实际场景中，这一步对计算性能有相当大的影响。那么接下来，我们就来讨论一下有关成本矩阵计算的影响。

二、成本矩阵的计算

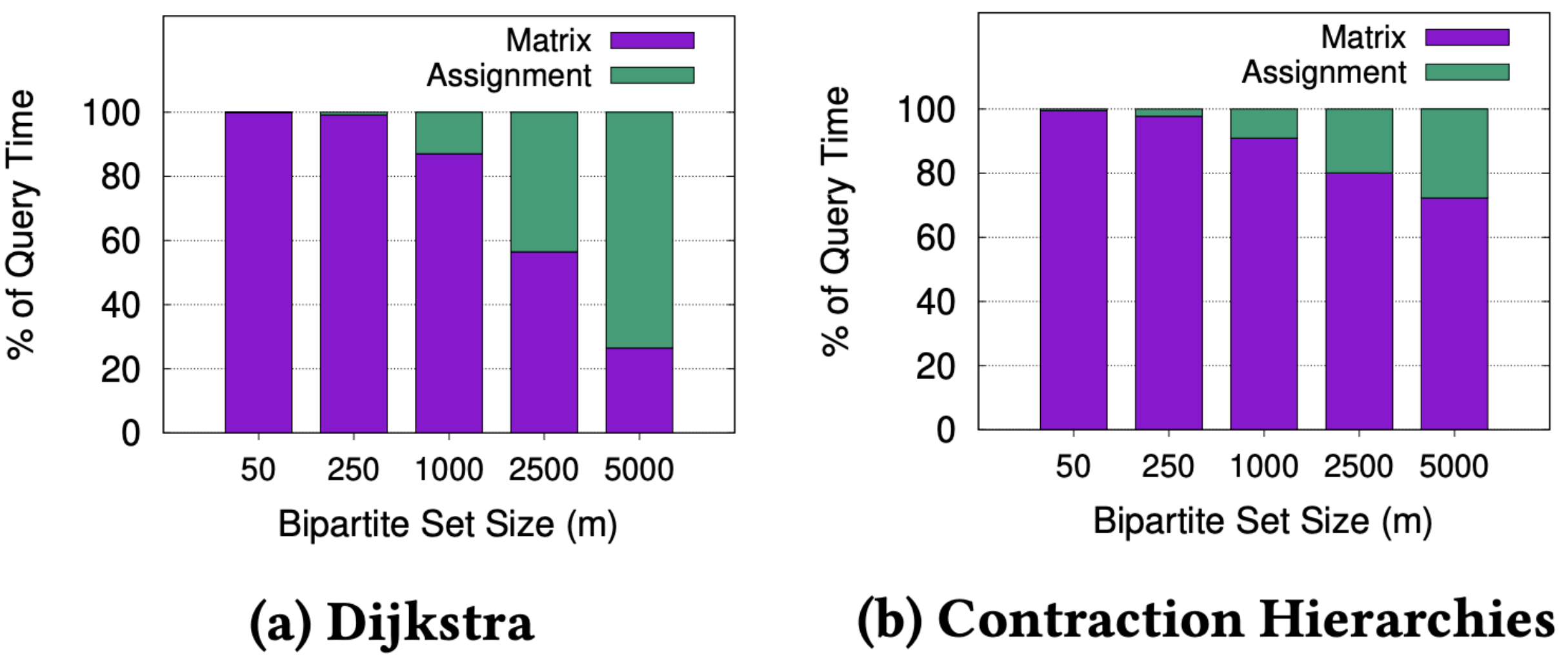
在这里插入图片描述
图2. 针对不同m值成本矩阵计算与分配的时间比

我们发现在以往解决分配问题的研究里大多都假设成本矩阵是作为输入给定的，但在实际场景中，我们观察到计算成本矩阵所需要的时间实际上是非常值得关注的。首先，司乘匹配是一个连续的过程，成本会随着司机的移动和新的订单的接收而不断变化。这意味着即使是间隔几秒钟，都有可能需要重新计算一次成本矩阵。其次，寻找单个乘客和司机之间的最短路径就需要不低的算力，而我们需要为所有可能的司机乘客对进行此操作，由此可想算力上可能会面临的挑战。作者发现在实际问题中，计算成本矩阵所需的时间甚至比计算最优分配所需的时间更长！

我们先浅浅地来从时间复杂度来看一下为什么是如此。如果 $m$ 代表我们试图匹配的司机/乘客的数量，那么KM算法的时间复杂度为 $O(m^3)$ ；如果 $n$ 代表道路网络中的顶点数，那么使用Dijkstra最短路径搜索算法计算成本矩阵的时间复杂度为 $O (mn l o g n)$ 。我们知道新加坡道路网络的节点数 $n$ 大约为400,000（对于更大的城市而言，这个数值更大），因此我们可以合理地期望在实际场景中（一般m小于1500）， $O (mn l o g n)$ 将占主导地位。我们在新加坡的道路网络上进行了实验来验证这一点，如图2所示。在图2（a）中，我们可以看到当 $m$ 小于等于2500时，计算矩阵的时间主导了寻找最优匹配的时间。即使我们使用像Contraction Hierarchies这样更现代快速的方法来计算最快路径，这样的观察结果仍然成立，如图2（b）所示。这表明如果我们能够减少矩阵计算时间，整体的匹配效率就可以得到显著提高。

三、匹配的空间局部性

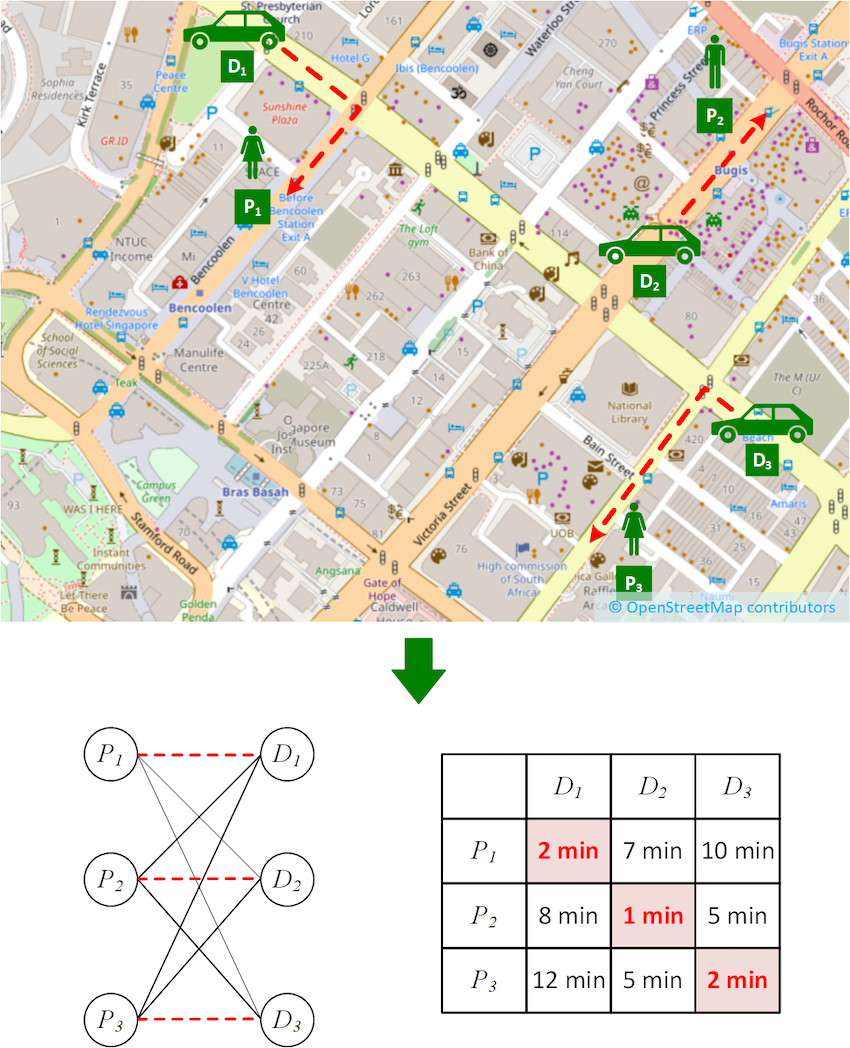
在这里插入图片描述
图3. 匹配的空间局部性场景示例

在研究乘客和司机的实际位置时，我们观察到了一个有趣的属性，我们将其称为“匹配的空间局部性”。我们发现，在最优匹配中，分配给每个司机的乘客是距离该司机最近的乘客之一（可能不是最近的）。这一点是非常直观的，因为乘客和司机是分布在整个城市的，而对于特定的司机来说，最优匹配不太可能出现在城市的另一边。

在图3中，我们可以看到一个展示这个属性的场景示例图，虽然这是一个理想化的示意图，但它也并没有太偏离实际情况。从所示的成本矩阵中，我们可以很容易地看出怎么样分配将提供最小的总行驶时间。现在，有了这样的直觉，我们想要考虑的问题是，我们到底有没有必要计算出完整的成本矩阵来找到最优匹配？比如，我们是否可以避免计算从 D3 到 P1 的成本，因为它们相隔太远，所以根本不太可能匹配？

四、改进后的KM算法

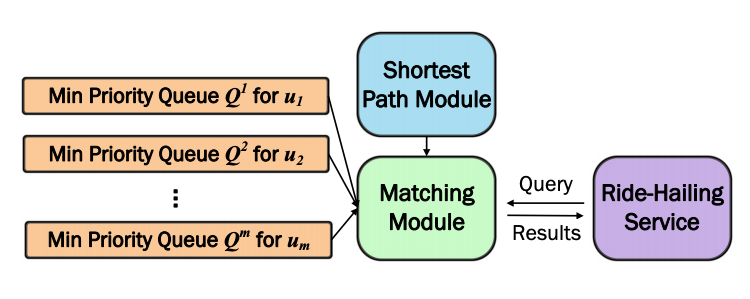
在这里插入图片描述
图4. 增量KM算法实现的框架

我们发现确实有一种方法可以利用匹配的空间局部性来减少成本计算的时间。作者提出了一种叫增量KM的算法，意思是仅在需要时才去计算成本，以有效的避免计算所有成本。修改过的KM算法采用了一种便捷的下界技术来实现这一点。我们用地标下界(Landmark Lower-Bounds, LLBs)作为最短路径的下界值，它所用到的核心思想其实就是三角不等式，不仅通俗易懂，还可以以较低的计算成本求出来。具体来讲，LLBs需要随机选择 𝑘 个“地标”顶点，并在离线预处理步骤中计算从每个地标到道路网络中所有顶点的距离并储存起来。在线上阶段，再用到任意地标顶点 𝑙 的距离以及三角不等式 $LB_l(q,p)=|d(l,q)-d(l,p)| \leq d(q,p)$ 就可以计算出任意两个顶点 $q$ 和 $p$ 之间的下界距离。通过考虑所有 𝑘 个地标的最大下界 $LB_{max}(q,p)=\max\limits_{l \in L}(|d(l,q)-d(l,p)|)$ ，我们发现即使对于较小的 𝑘 值，仍然可以计算出令人惊讶准确的最短路径下界。

除此之外，我们还用到数据库领域一个非常经典的概念k-最近邻搜索来实现每个司机 $u_i$ 的优先队列 $Q_i$ ，如图4所示。这些优先队列通过行驶时间的下界来检索最近的乘客，而优先队列的顶部则储存着所有尚未检索的乘客的行驶时间下界。KM算法可以用相关优先队列的下界来避免计算精确成本，然后照常运行。对于一些情况下下界对于KM计算最优匹配不够准确的问题，我们进而提出了一些改进规则。一旦触发了一条规则，我们就通过检索顶部元素并计算其精确成本来改进队列，这就是为什么我们称之为“增量”成本计算。如果你对具体细节感兴趣，可以在原文中去更深入地了解改进规则、算法的内部运作以及数学证明。

我们发现增量KM算法能够生成与原始KM算法完全相同的结果！它只是采用了一种乐观的增量方式完成，希望可以在不计算所有成本的情况下找到结果，这非常适用于我们打车问题中的匹配的空间局部性。我们不仅节约了大量计算精确成本的时间，也避免了计算那些距离很远的乘客的行驶时间（往往耗费更大的计算资源）。

五、实验结果

我们通过实验对比来验证所提出算法的实际性能。我们实现了两个版本的增量KM算法，它们分别在优先队列和所使用的最短路径算法的实现上有所不同。

IKM-DIJK：使用Dijkstra算法计算最短路径，优先队列即是从每个司机展开的Dijkstra搜索优先队列，这跟常规KM算法相比没有额外的花费。
IKM-GAC：使用最先进的下界技术COLT来实现优先队列和一种快速计算最短路径的方法G-tree。每个分配都必须构建COLT索引，这个会包含在所有运行时间中。

我们将提出的两个算法与使用Dijkstra和G-tree分别计算整个成本矩阵的常规KM算法进行比较并在新加坡真实的道路网络上进行了实验。除此之外，我们还用到了一个包括2018年12月的7天内的Grab打车订单。

性能评估：

我们首先选择一个以秒为单位大小为 $W$ 的窗口，然后在一个随机选择的大小为 $W$ 的窗口中对所有预订进行批量处理，并使用这些订单中的乘客和司机的位置来构建二分图集合。接下来，我们用每种算法去找到一个最优匹配，并在多个随机选择的窗口上对各个度量标准的结果取均值。

在这里插入图片描述
图5. 每种算法计算成本矩阵的平均比例 v.s. 窗口大小

在图5中，验证了我们提出的算法的确与其对应的方法相比计算了更少的精确成本（原始的KM算法计算了100%的矩阵）。

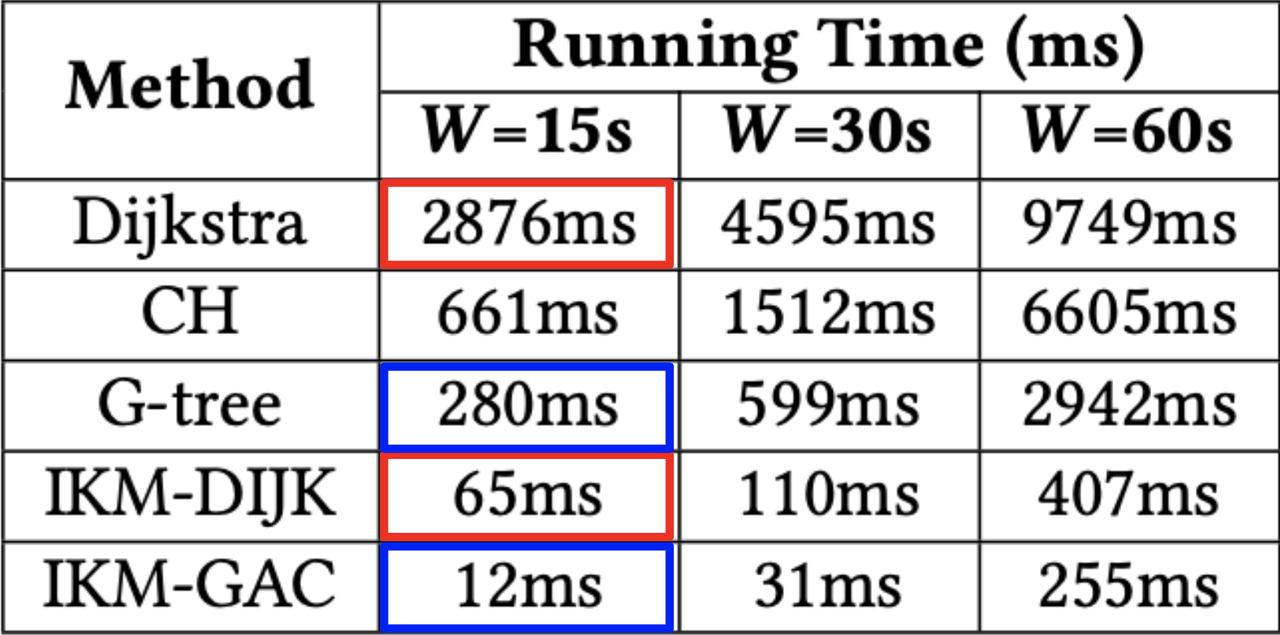
在这里插入图片描述
图6. 每种算法寻找最优分配的平均时间 v.s. 窗口大小

在图6中，我们可以看到每种算法的运行时间。图中的结果证实，减少精确成本的计算显著减少了超过一个数量级的运行时间，这也验证了节省的时间是大于任何添加的额外时间的。请注意，IKM-DIJK的改进本质上没有消耗额外的算力成本！另外值得注意的是，使用IKM-GAC可以实现非常低的运行时间。

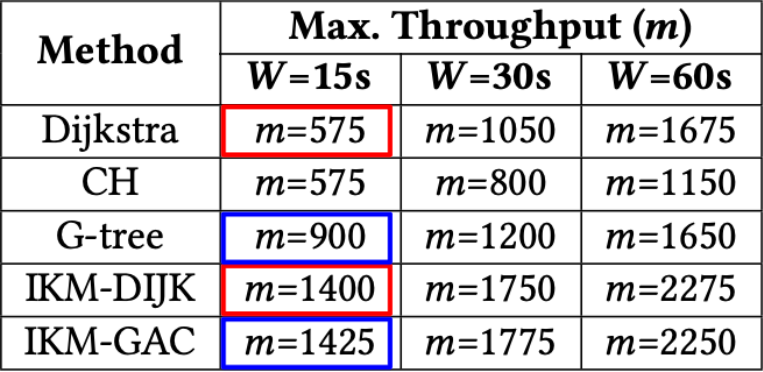
在这里插入图片描述
图7. 每种算法支持的最大吞吐量 v.s. 窗口大小

在图7中，我们展示了每种算法支持的最大吞吐量，即在时间窗口 $W$ 内可以批量处理的乘客/司机的最大数量。如图所示，我们的算法可以支持明显更高的吞吐量。

六、总结

总的来说，计算分配成本确实对寻找最优分配的运行时间产生了显著影响。然而，我们发现通过利用实际分配问题中的匹配的空间局部性，可以通过修改KM算法以增量的方式运作，来避免计算非必要的精确成本。

而且，值得一提的是，我们提出的方法框架还可以适用于除了司乘匹配外其他用到分配问题的场景中。

参考文献：
[1] Tenindra Abeywickrama, Victor Liang, and Kian-Lee Tan. 2021. Optimizing bipartite matching in real-world applications by incremental cost computation. Proc. VLDB Endow. 14, 7 (March 2021), 1150–1158
[2] https://engineering.grab.com/using-real-world-patterns-to-improve-matching
[3] H. W. Kuhn. 1955. The Hungarian method for the assignment problem. Naval Research Logistics Quarterly 2, 1-2 (1955), 83–97
[4] Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1, 269–271 (1959)
[5] Robert Geisberger, Peter Sanders, Dominik Schultes, and Daniel Delling. 2008. Contraction Hierarchies: Faster and Simpler Hierarchical Routing in Road Networks. In WEA. 319–333
[6] Ruicheng Zhong, Guoliang Li, Kian-Lee Tan, Lizhu Zhou, and Zhiguo Gong. 2015. G-Tree: An Efficient and Scalable Index for Spatial Search on Road Networks. IEEE Trans. Knowl. Data Eng. 27, 8 (2015), 2175–2189
[7] Tenindra Abeywickrama, Muhammad Aamir Cheema, and Sabine Storandt. 2020. Hierarchical Graph Traversal for Aggregate k Nearest Neighbors Search in Road Networks. In ICAPS. 2–10