题目描述
力扣地址
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
示例 1:
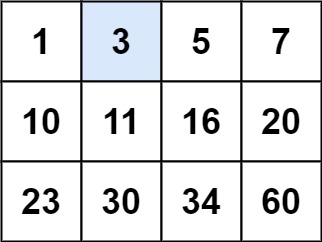
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3 输出:true
示例 2:
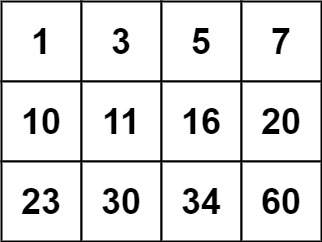
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-104 <= matrix[i][j], target <= 104
以右上或左下为起点进行搜索
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = matrix.length;int col = matrix[0].length;int i = 0;int j = col-1;while(i>-1 && i<row && j>-1 && j<col){if(matrix[i][j] < target){i++;}else if(matrix[i][j] > target){j--;}else{return true;}}return false;}
}这种解法效率不高需要用二分来优化,这道题目描述的矩阵具有两个关键属性:
- 每行中的整数从左到右按非严格递增顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
由于这两个属性,虽然矩阵是二维的,但它可以被视为一个一维的有序数组。具体来说,如果我们将这个矩阵“展开”成一个一维数组,这个数组将是有序的。这使得我们可以在这个虚拟的一维数组上应用二分查找算法。
class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = matrix.length;int col = matrix[0].length;int left = 0;int right = row * col - 1;while (left <= right) {int midIndex = left + (right - left) / 2;int midValue = matrix[midIndex / col][midIndex % col];if (midValue == target) {return true;} else if (midValue < target) {left = midIndex + 1;} else {right = midIndex - 1;}}return false;}
}LeetCode378之有序矩阵中第 K 小的元素(相关话题:优先队列,二分)
这道题不具备每行的第一个整数大于前一行的最后一个整数这个属性所以不能直接把二维矩阵转化为一维数据进行二分。而是直接对矩阵里的最大值和最小值进行二分。
相关文章
LeetCode之团灭旋转数组(相关话题:减治,二分,分治)_target的最小数的下标-CSDN博客
LeetCode287之寻找重复数(相关话题:二分查找,快慢指针)-CSDN博客
LeetCode287之寻找重复数(相关话题:位运算,抽屉原理)_442. 数组中重复的数据 leetcode python-CSDN博客
算法模板(一)(相关话题:二分搜索)_if (left >= nums.length || nums[left] != target) r-CSDN博客
LeetCode378之有序矩阵中第 K 小的元素(相关话题:优先队列,二分)_java给你一个 n x n 矩阵 matrix ,其中每行和每列元素均按升序排序,找到矩阵中第-CSDN博客
LeetCode1095.之山脉数组中查找目标值(相关话题:多重二分)-CSDN博客