详解协方差矩阵，相关矩阵，互协方差矩阵（附完整例题分析）【2】-编程知识

一. 写在前面

二. 相关矩阵（Correlation Matrix）

三. 实战分析

例题1

（1）均值的关系

（2）协方差的关系

（3）小结

例题2

小结

四. 补充

一. 写在前面

有关协方差矩阵和互协方差矩阵的介绍可以看这篇博客：

详解协方差矩阵，相关矩阵，互协方差矩阵（附完整例题分析）【1】-CSDN博客

本篇文章主要关注相关矩阵以及例题分析。例题会总结这两篇文章的内容。

二. 相关矩阵（Correlation Matrix）

给定数据矩阵如下：

$\bold{X}=\begin{bmatrix} x_{11} & x_{12} & \cdots &x_{1p} \\ x_{21} & x_{22} & \cdots &x_{2p} \\ \vdots & \vdots &\ddots &\vdots \\ x_{n1} & x_{n2} & \cdots &x_{np} \end{bmatrix}$

样本向量的均值头上会有个横线，如 $\bar{\vec x}$ ，将样本的协方差记为S，计算公式快速复习下：

$\bold{S}=\frac{1}{n-1}\sum_{i=1}^n(\vec x_i-\bar{\vec{x}})(\vec x_i-\bar{\vec{x}})^T$

每个向量的都是p维的，也就是实际有p个随机变量，令 $\bar x_j$ 代表第j个随机变量的均值，j的取值有p个，也就是 $j=1,2,\cdots,p$ 。根据上一篇文章的分析，协方差矩阵对角线处的元素 $\sqrt{s_js_j}$ 代表变量j的标准差。

我们知道任何正态分布，都可以变成均值为0，方差为1的标准正态分布。借助此思想，我们来对数据矩阵中的元素进行标准化，如下：

$z_{ij}=\frac{x_{ij}-\bar x_j}{\sqrt{s_{jj}}}$

原始数据矩阵，现在变成：

$\bold{Z}=\begin{bmatrix} z_{11} & z_{12} & \cdots &z_{1p} \\ z_{21} & z_{22} & \cdots &z_{2p} \\ \vdots & \vdots &\ddots &\vdots \\ z_{n1} & z_{n2} & \cdots &z_{np} \end{bmatrix} =\begin{bmatrix} \vec z_1^T\\ \vec z_2^T\\ \vdots\\ \vec z_n^T \end{bmatrix}$

新数据矩阵的协方差与原始数据矩阵的协方差之间有什么关系呢？

取 $\bold{Z}$ 的第i行，代表第i次取样，如下：

$\begin{bmatrix} z_{i1}\\ z_{i2}\\ \vdots\\ z_{ip} \end{bmatrix}= \begin{bmatrix} (x_{i1}-\bar x_1)/\sqrt{s_{11}}\\ (x_{i2}-\bar x_2)/\sqrt{s_{22}}\\ \vdots\\ (x_{ip}-\bar x_p)/\sqrt{s_{pp}}\\ \end{bmatrix}$

对矩阵进行分解成一个对角阵和列向量：

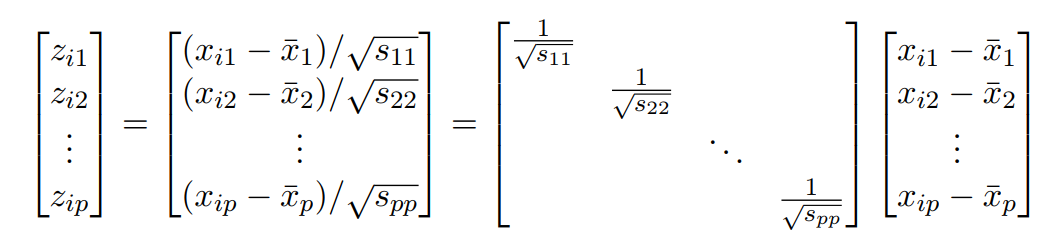
此处的对角阵每一个元素都是开根号的格式，且每个元素都被取了倒数，所以令：

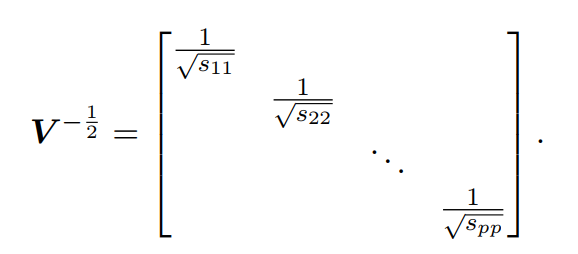
简单分析：矩阵的逆对应每个元素的负一次方，矩阵的开根号，对应元素的开根号。以上运算告诉我们向量 $\vec z_i$ 与向量 $\vec x_i$ 的关系可以用矩阵V来衡量，n个样本向量都是如此，如下：

$\vec z_i=\bold{V}^{-\frac{1}{2}}(\vec x_i-\bar{\vec x})=\bold{V}^{-\frac{1}{2}}\vec x_i-\bold{V}^{-\frac{1}{2}}\bar{\vec x}$

把n个向量 $\vec z_i$ 相加并处以n即可得到对应的均值，计算如下：

$\bar{\vec {z_i}}=\bold{V}^{-\frac{1}{2}}(\bar{\vec x}-\bar{\vec x})=0$

不难理解，因为向量z为标准化的结果，所以均值为0.

根据z与x之间的线性关系，新的数据矩阵的协方差矩阵，可以计算如下：

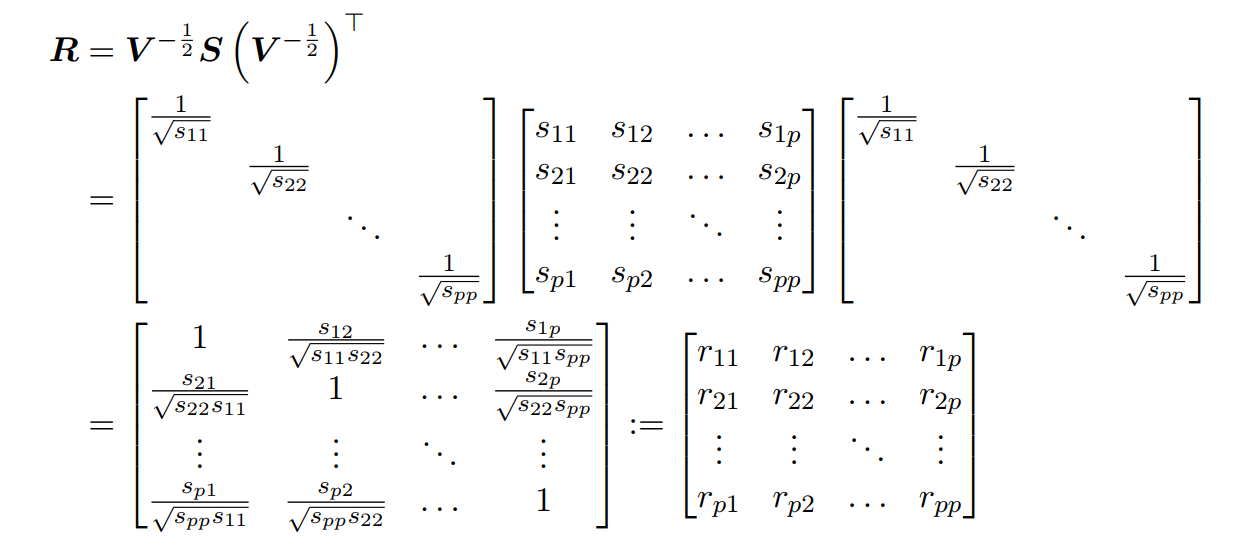
其实此矩阵R就是原始数据矩阵X的相关矩阵（correlation matrix）。

有关这个矩阵的计算公式分析，大家还是可以看我之前的那篇博客。

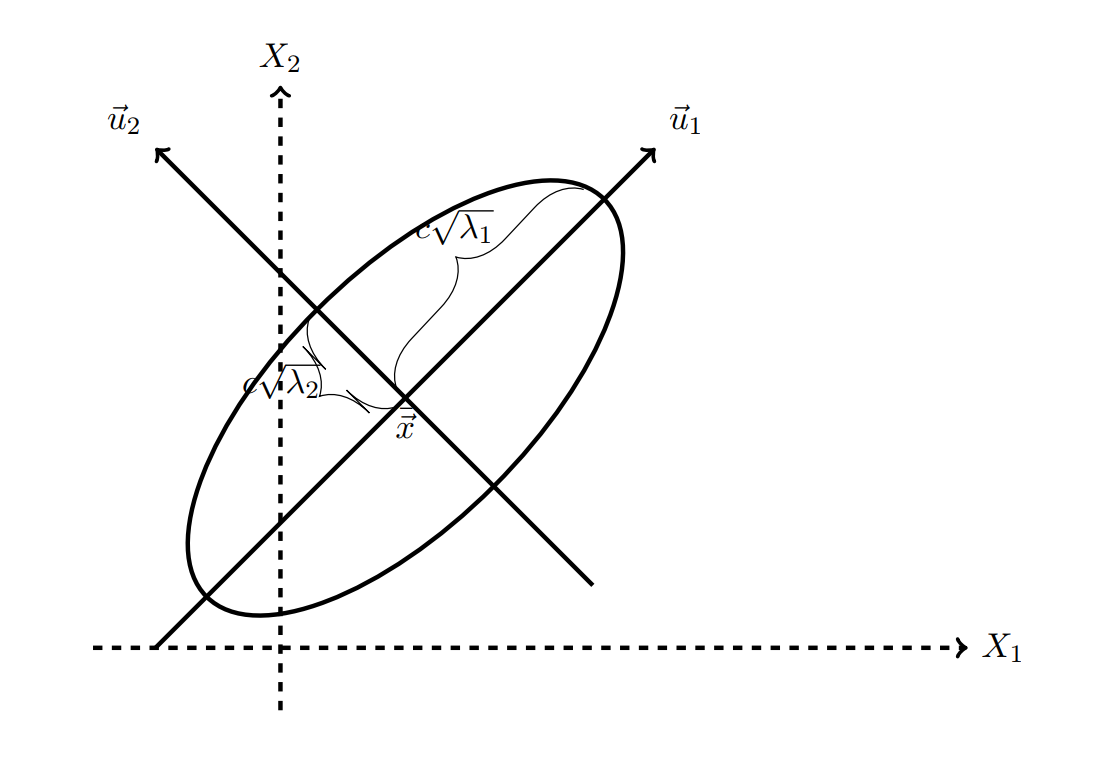
其实有关协方差矩阵可能会出现半正定矩阵的情况，这个时候就会出现Mahalanobis distance和mean-centered ellipse，由于篇幅关系，暂时就先放个直观理解的图，如果有人关心的话，以后再补上详细文字解释。

三. 实战分析

例题1

给定二维的向量样本，抽取n次，形成如下数据矩阵：

$\bold{X}=\begin{bmatrix} x_{11} & x_{12}\\ x_{21} & x_{22}\\ \vdots&\vdots \\ x_{n1} & x_{n2}\\ \end{bmatrix}$

样本X对应的均值向量为 $\bar{\vec x}$ ，协方差矩阵为 $\bold{S}_{\vec x}$ 。假定存在另外一个样本Y，Y与X之间满足如下关系：

尝试计算样本Y的均值与协方差。

解：

（1）均值的关系

观察Y与X的关系，发现它们样本之间满足线性关系，如下：

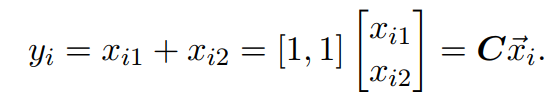
其中矩阵 $\bold{C}=\begin{bmatrix} 1 & 1 \end{bmatrix}$

可以发现样本x为一个二维向量，样本y为一个标量。由此， $y_1,\cdots,y_n$ 的样本均值，可计算如下：

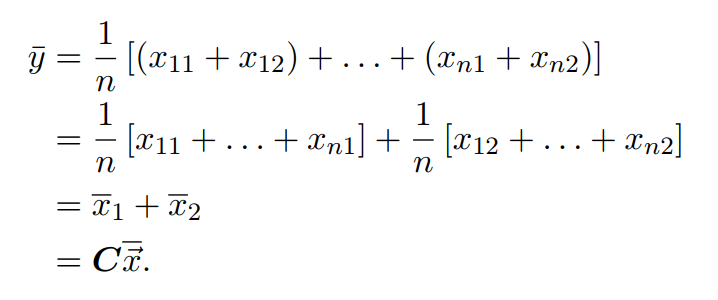
第一个等号：均值的定义；

第二个等号：向量X本质有两个变量，分成两部分；

第三个等号：两个变量的均值，此时的两个变量均为变量；

第四个等号：样本y与x的均值关系，可以用一个矩阵C来衡量；

备注：矩阵C为一个行向量， $\bar{\vec x}$ 为一个列向量，两者相乘为一个数。

（2）协方差的关系

因为样本y的本质为标量，所以y得协方差其实就是y的方差。将 $y_1,\cdots,y_n$ 的方差记为 $s_y^2$ ，由此进行计算：

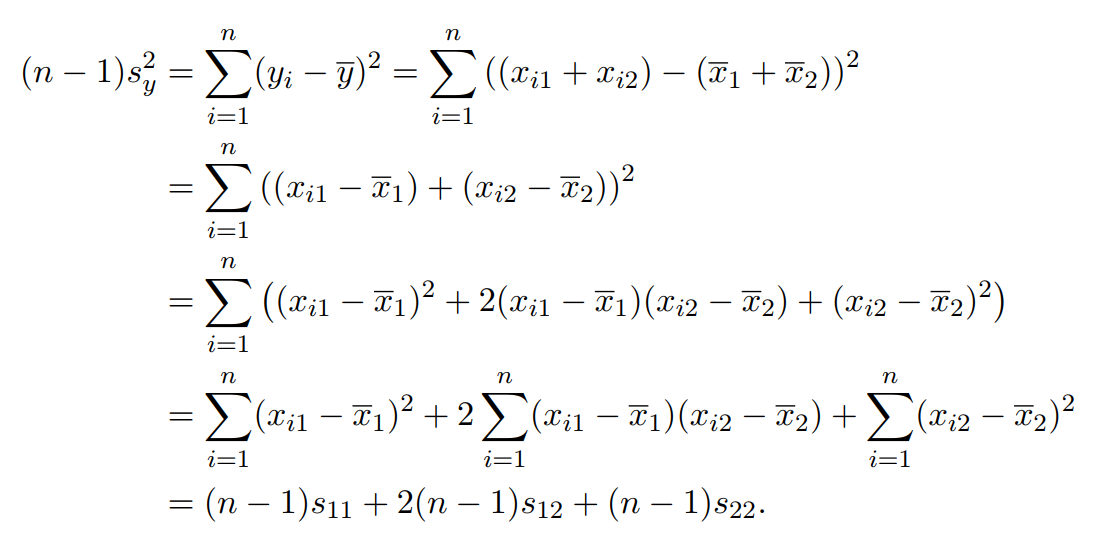
第一行等号：样本y方差的定义；将数据 $y_i$ 与 $\bar y$ 分别代入；

第二行等号：样本向量x的两个变量分别合并；

第三行等号：完全平方差公式；

第四行等号：求和符号拆分成三个；

第五行等号：

向量x的协方差为2行2列的矩阵。该矩阵为对称矩阵，根据对协方差矩阵的理解可得：

$\sum_{i=1}^n(x_{i1}-\bar x_1)^2=s_{11}$

$\sum_{i=1}^n(x_{i1}-\bar x_1)(x_{i2}-\bar x_2)=s_{12}=s_{21}$

$\sum_{i=1}^n(x_{i2}-\bar x_2)^2=s_{22}$

其中 $s_{11}$ 代表协方差矩阵第一行第一列的元素，以此类推。

我们知道方程的运算与代数的运算之间是有关系的，由此可进行总结如下：

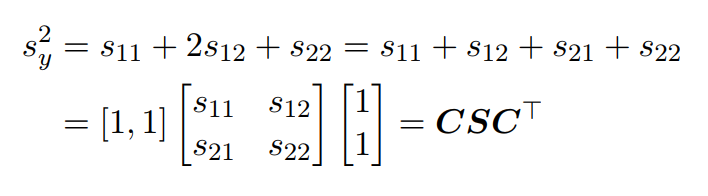
此处的运算就是单纯的线性代数的知识，就不做过多阐述。需要注意的是右边矩阵运算完的结果为一个标量。

（3）小结

已知向量型随机变量X，对其做一些线性变化形成随机变量Y：

$\vec Y=\begin{bmatrix} Y_1\\ \vdots \\ Y_q \end{bmatrix}=C\vec X+\vec d$

其中 $\bold{C}\in R^{q\times p},\vec d\in R^q$ 。

$\bar{\vec y}=\frac{1}{n}\sum_{i=1}^n(\bold{C}\vec x_i+\vec d)=\bold{C}(\frac{1}{n}\sum_{i=1}^n\vec x_i)+\vec d=\bold{C}\bar{\vec x}+\vec d$

换句话说，一旦给出了X的均值，我们可以利用 $\bar{\vec y}=\bold{C}\bar{\vec x}+\vec d$ 求y的均值。

量Y与X之间的协方差矩阵满足：

$\bold{S}_y=\bold{CS}_x\bold{C}^T$

例题2

已知变量 $\vec X=\begin{bmatrix} X_1\\ X_2\\ X_3\\ X_4 \end{bmatrix}$ ，可形成数据矩阵 $\bold{X}\in R^{n,4}$ ，已知其协方差矩阵如下：

$\begin{bmatrix} 2 & 0&0 &0 \\ 0& 2&1 & 0\\ 0 & 1 & 2 & 1\\ 0&0 &1 &2 \end{bmatrix}$

试求 $\begin{bmatrix} X_1\\ X_3 \end{bmatrix}$ 与 $\begin{bmatrix} X_2\\ X_4 \end{bmatrix}$ 之间的互协方差矩阵（cross-covariance matrix）。

解：

将 $\begin{bmatrix} X_1\\ X_3 \end{bmatrix}$ 看成一个新的变量，将 $\begin{bmatrix} X_2\\ X_4 \end{bmatrix}$ 看成另一个新的变量，两者合并如下：

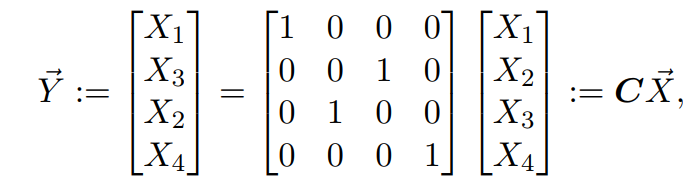
第一个等号：变量Y的定义

第二个等号：变量Y与X之间的关系，注意列向量中 $X_1\sim X_4$ 的顺序；

由此便找到了变量Y与X之间的关系。根据例题1的结论，可计算变量的Y的协方差矩阵如下：

对变量Y进行分割：

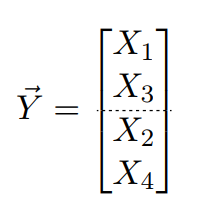
根据协方差分割的思想，对Y的协方差矩阵进行分割如下：

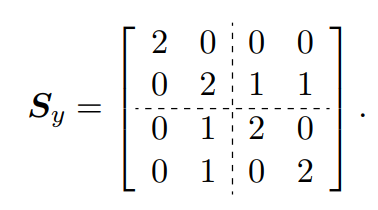
由此 $\begin{bmatrix} X_1\\ X_3 \end{bmatrix}$ 与 $\begin{bmatrix} X_2\\ X_4 \end{bmatrix}$ 之间的互协方差矩阵（cross matrix）如下：

$\begin{bmatrix} 0 &0 \\ 1 &1 \end{bmatrix}$

小结

给定一个向量型的随机变量：

$\vec X=\begin{bmatrix} X_1\\ X_2\\ \vdots\\ X_p \end{bmatrix}$

进行分割：

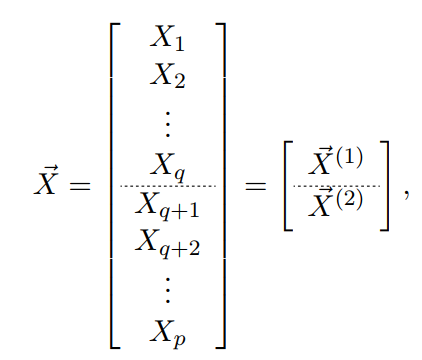
样本均值可得：

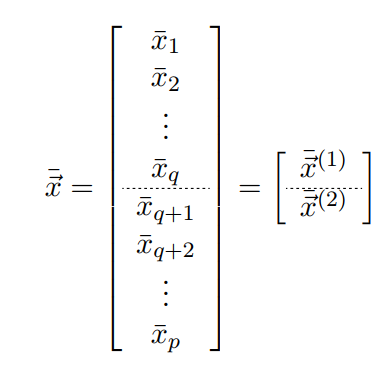
协方差的割分如下：

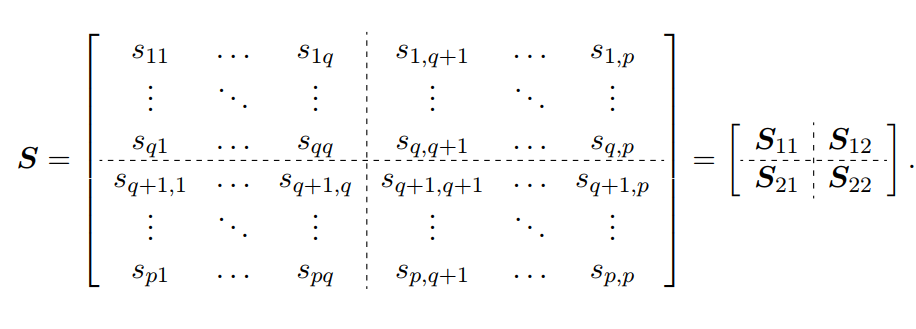
$\bold{S}_{11}$ 就是样本 $\vec X^{(1)}$ 的协方差矩阵；

$\bold{S}_{22}$ 就是样本 $\vec X^{(2)}$ 的协方差矩阵；

$\bold{S}_{12}$ 和 $\bold{S}_{21}$ 则可以看成 $\vec X^{(1)}$ 与 $\vec X^{(2)}$ 之间的互-协方差矩阵；

四. 补充

对于二维随机向量(X,Y)来说，数学期望E(X), E(Y)只反映了X与Y各自的平均值，方差D(X), D(Y)只反映了X与Y各自离开其均值的偏离程度. 但它们对X与Y之间相互关系不提供任何信息.

二维随机向量(X,Y)的概率密度 f (x,y)或分布列 $p_{ij}$ 全面地描述了(X,Y)的统计规律，也包含有X与Y之间关系的信息. 我们希望有一个数字特征能够在一定程度上反映这种联系. 协方差和相关系数就是用来描述X与Y之间相互关系的数字特征.