个人主页:Lei宝啊
愿所有美好如期而遇
目录
本题链接
输入描述
输出描述
算法分析
算法一:暴力求解
算法二:前缀和
预处理前缀和dp表
使用前缀和dp表
解题源码
我们以一道题目为例详解一维前缀和原理。
本题链接
【模板】前缀和_牛客题霸_牛客网
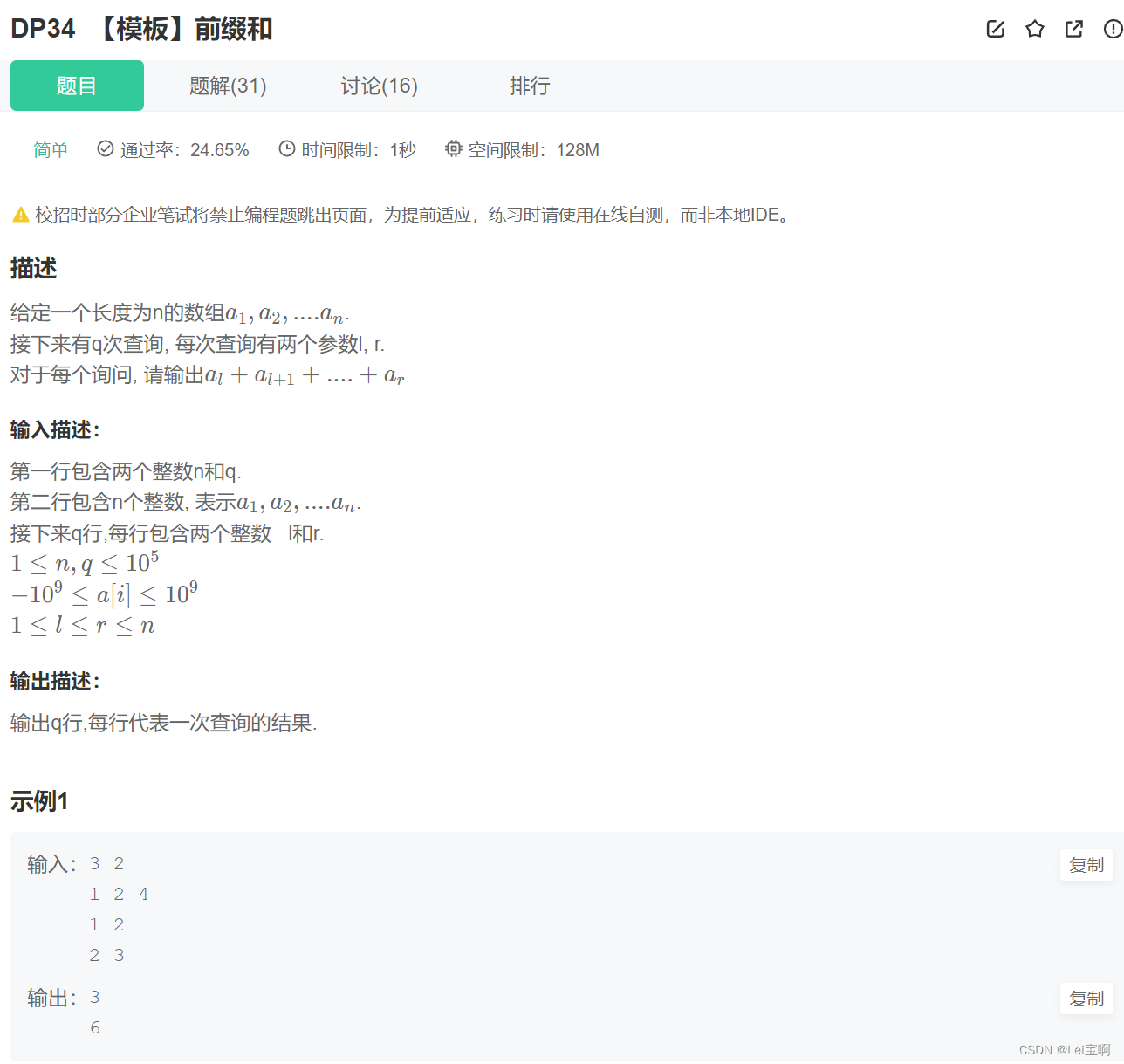
输入描述
首先第一行输入两个整数,n和q,n是要输入的数组的元素个数,q是要查询的次数,查询时输入l和r,代表着要查询的数组区间
比如:我们的示例:
- n = 3,我们输入的数组元素就有三个:1 2 4
- q = 2,我们就需要查找两次,l和r也就会更新两次,要查询的数组区间也就是[1,2] [2,3]
值得注意的是n和q都大于等于1,至于为什么要这么给,我们后面讲算法会说到。
输出描述
返回要查询的数组区间内所有元素值的和。
算法分析
算法一:暴力求解
直接遍历数组,从给定区间开始遍历q次,我们分析一下时间复杂度:首先有q次的遍历,并且我们考虑最坏的情况,就是每次数组都是从头遍历到尾,时间复杂度就为O(q*N),按我们本题最大的q和n来看,这么干绝对是超时的。
算法二:前缀和
预处理前缀和dp表
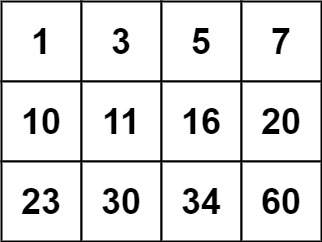
类似于动态规划的dp表,这里的dp表每个元素都表示一个状态,由于我们的n是从1开始的,那我们的dp[1]就用来表示区间[1,1]的和,dp[1]表示区间[1,2]的和,看图更直观些:
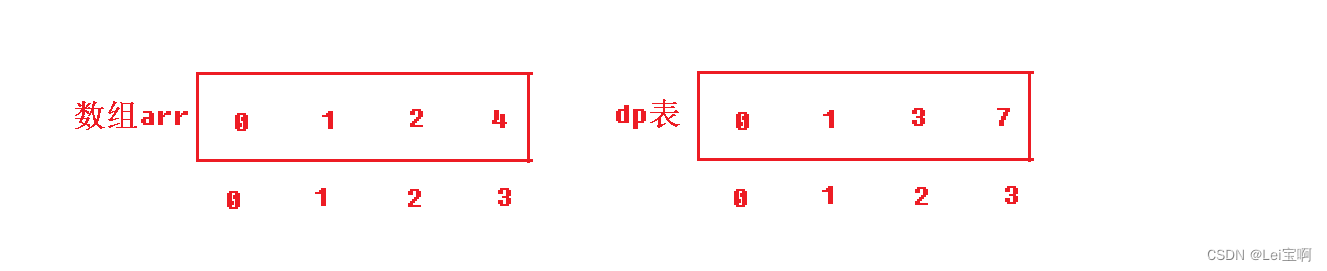
我们可以用一个变量sum来表示和,然后通过遍历数组给dp表赋值。
使用前缀和dp表
那么我们如何使用dp表来求取数组区间的元素和呢?
我们dp表第i个位置就表示从下标0到下标i所有元素的和,比如我们要算[2,3]区间,也就是求这个区间的元素和,就是dp[3]-dp[1],我们也就能推知一个公式:
区间和 = dp[r] - dp[l-1];
解题源码
#include <iostream>
#include <vector>
using namespace std;int main()
{int n = 0, q = 0;cin >> n >> q;vector<int> v(n+1,0);for(int i=1; i<v.size(); i++) cin >> v[i];//创建dp表,并填值vector<long long> dp(n+1,0);long long sum = 0;for(int i=1; i<v.size(); i++){sum += v[i];dp[i] = sum;}//查询while(q--){int l, r;cin >> l >> r;cout << dp[r] - dp[l-1] <<endl; }
}
// 64 位输出请用 printf("%lld")