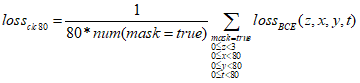参考资料：生物统计学

       方差分析是将总变异分解为组间变异的方差和组内变异的方差，并通过F检验推断处理效应是否显著的过程，而方差是通过平方和与自由度计算出来的，所以方差分析首先需要进行平方和与自由度的分解。具体步骤如下：

1、平方和的分解

       为了方便表述，用表示全部观测值的平均数，表示第i组的平均数，T表示全部观测值的总和，表示第i组的何。

       全部观测值的总变异的平方和称为总平方和，记为，公式可表示为：

因为：

且：

所以

其中，为各组平均数与总平均数间的离差平方和，称为处理平方和或组间平方和，反应不同处理之间的变异，记为，即

为各组内观测值与该组的平均数间离差平方和的总和，简称误差平方和或组内平方和，反应随机误差引起的变异，记为，即

最终可简写为

由于在实际计算时，误差平方和是总平方和减去处理平方和后的剩余部分，所以也称为剩余平方和，所以误差平方和的计算公式可写为：

平方和可以不计算平均数而直接用原始数据计算，这是需要先计算矫正数C，

2、自由度的分解

总自由度：

处理自由度：

误差自由度：

总平方和、总自由度的可分解性，或反过来叫各分量平方和、各分量自由度的可加性，这是Fisher创建方差分析方法时发现的规律，是方差分析原理的核心内容。

3、计算均方

平方和与自由度分解完成后，根据各自的平方和及自由度计算均方（就是方差，方差分析中习惯称为均方，记为MS）。

处理均方：

误差均方：

误差均方实质上是各组内方差按自由度算得的加权平均数，所以也称为合并方差。

4、计算F统计量

F统计量为处理均方和误差均方之比。

       在进行两个样本方差的同质性检验时，要求用大方差做分子 、小方差做分母，但在方差分析中，始终是用处理均方做分子、误差均方做分母。如果处理均方小于误差均方，则直接推断处理效应（样本平均数间的差异）不显著。

        若，则表示处理间差异显著。

5、方差分析表

excel公式操作步骤：

数据分析工具操作步骤：

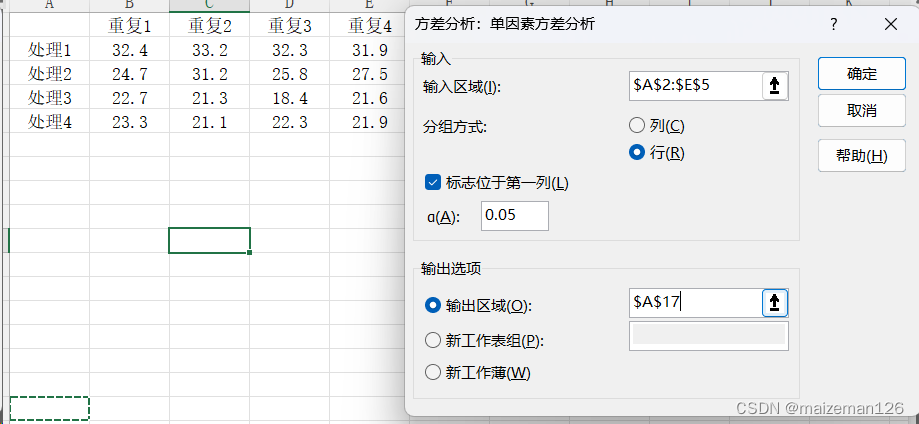
1、数据分析工具中选择“方差分析：单因素方差分析”

2、打开单因素方差分析对话框

选择数据区域，本此选择区域包含处理名称，和处理的数据是按行分布的。

故对话框中，分组方式选择“行”；勾选“标志位于第一列”

 3、查看分析结果