六、 实现细节
都有哪些开源的卷积神经网络实现

caffe中卷积神经网络各个层(卷积层、全连接层、池化层、激活函数层、内基层、损失层等)

Caffe2 与caffe 对比
caffe2 开源吗
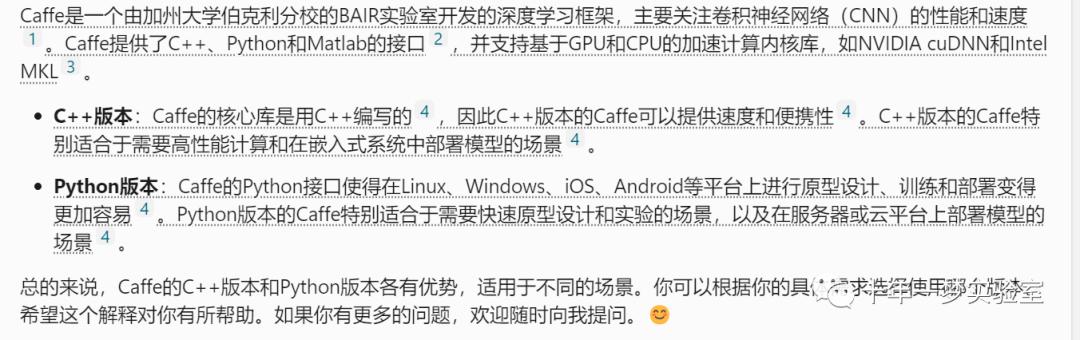
使用caffe的c++ 版本和python版本,分别适用于哪些场景

6.1 卷积层

在进行预测时,训练时 正向传播区别

采用矩阵乘法的优势

6.2 激活函数
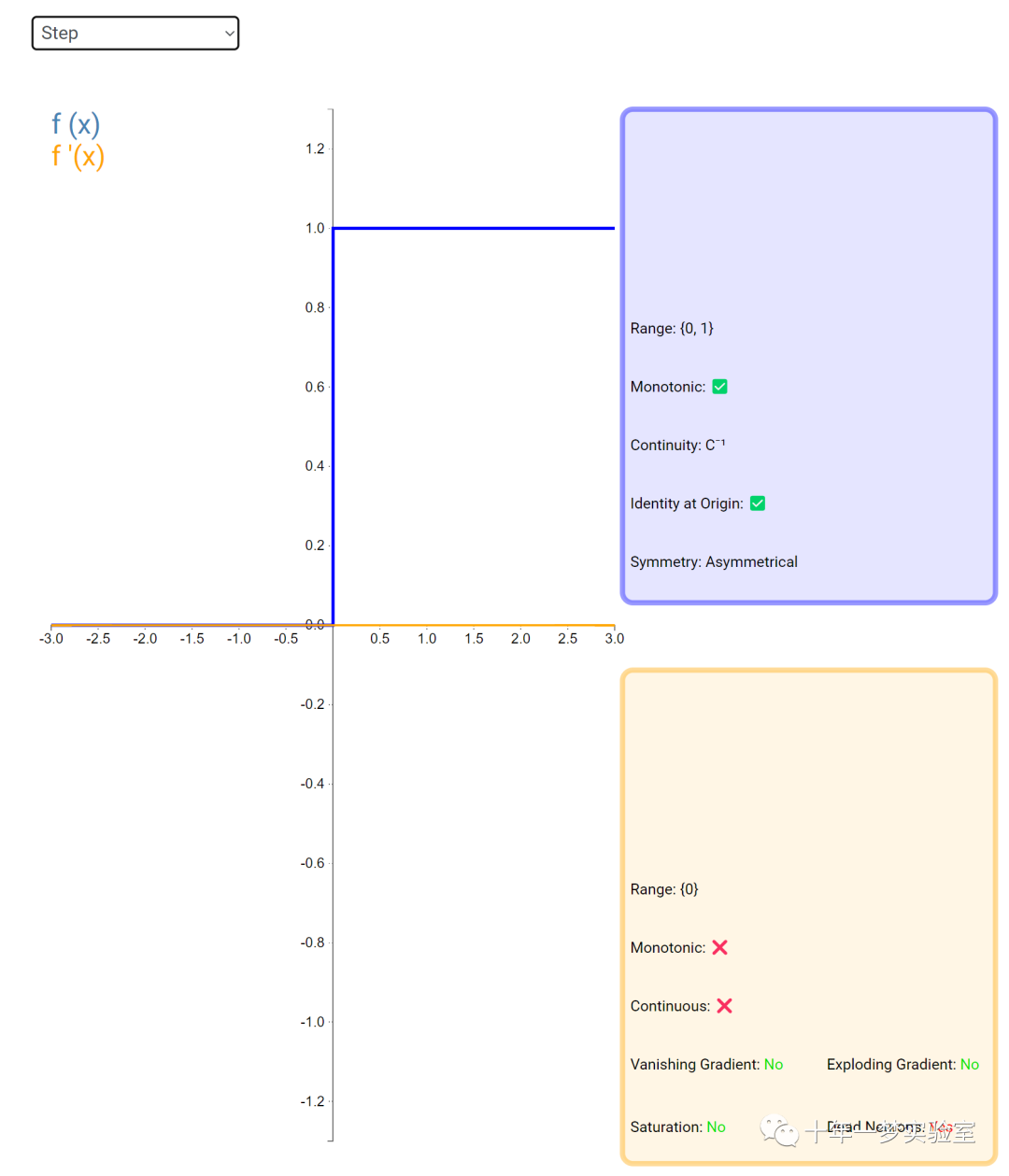
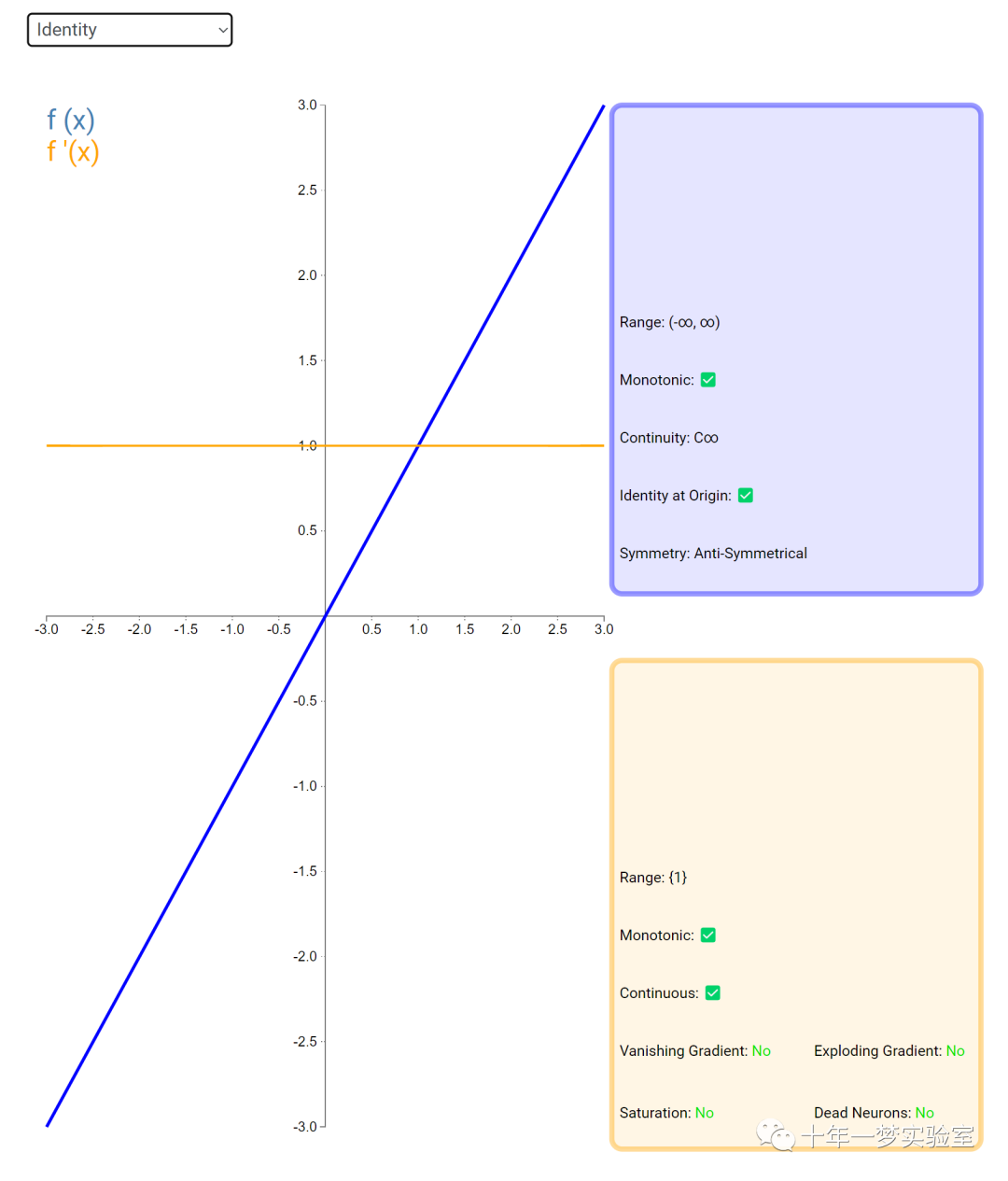
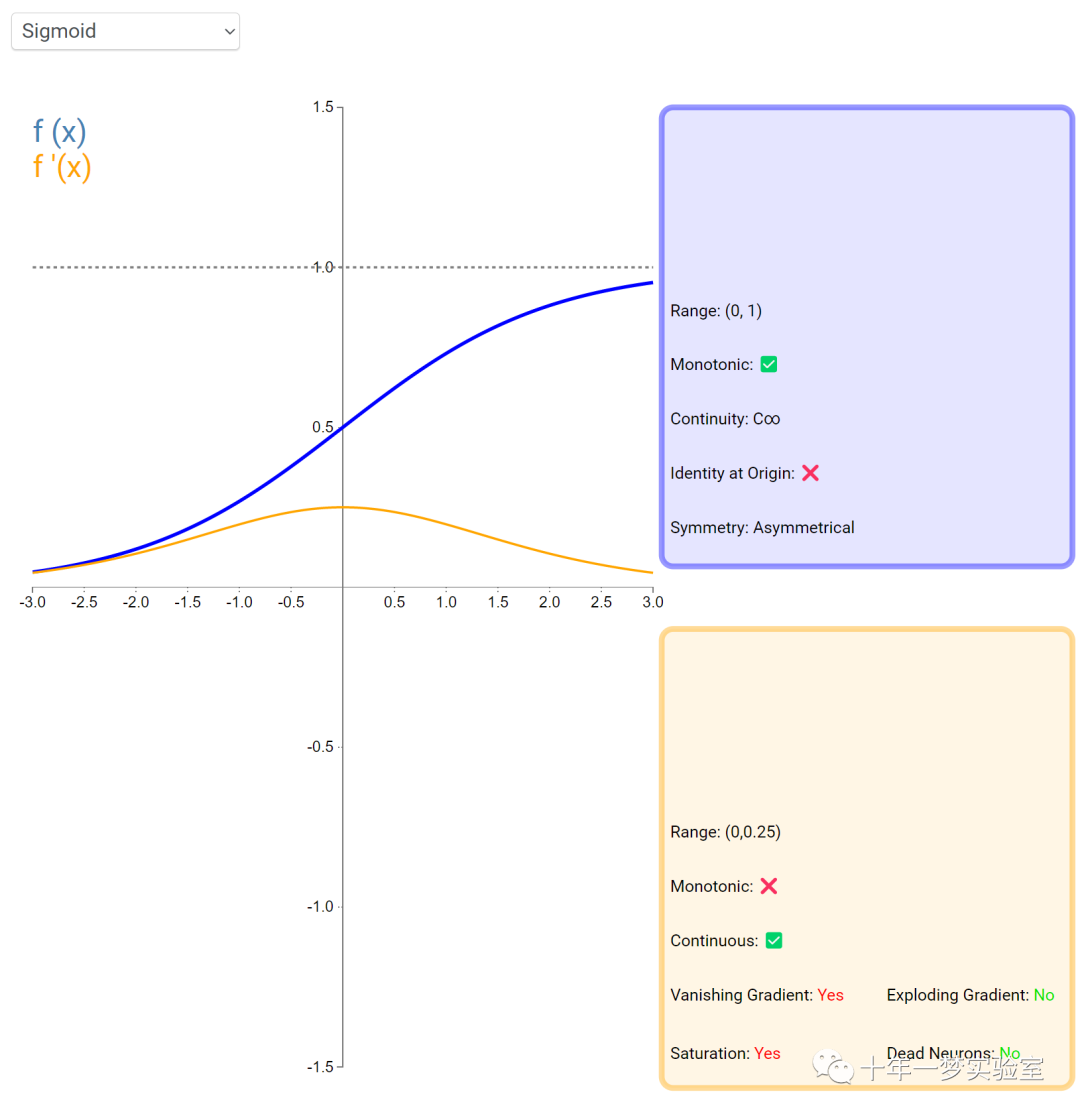
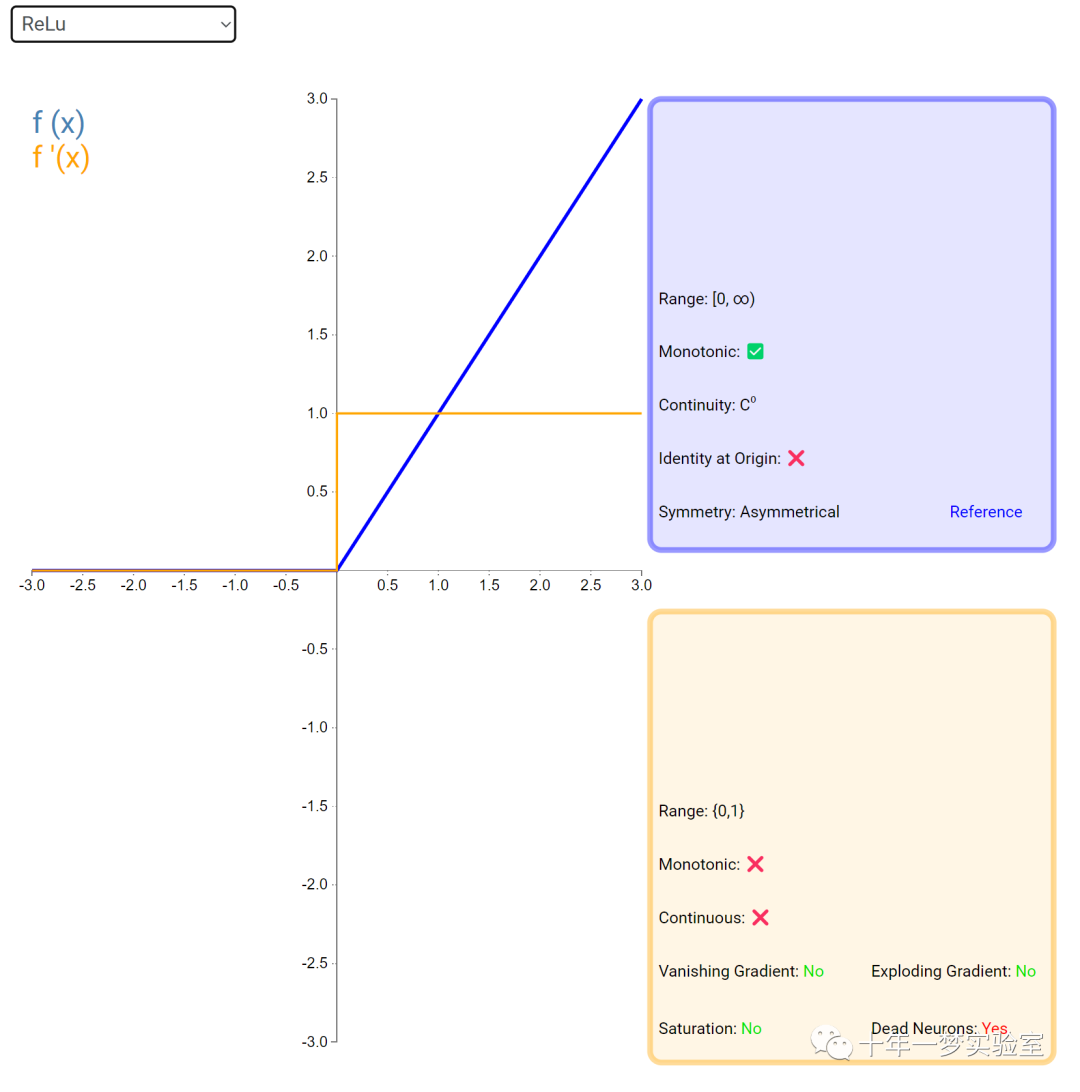
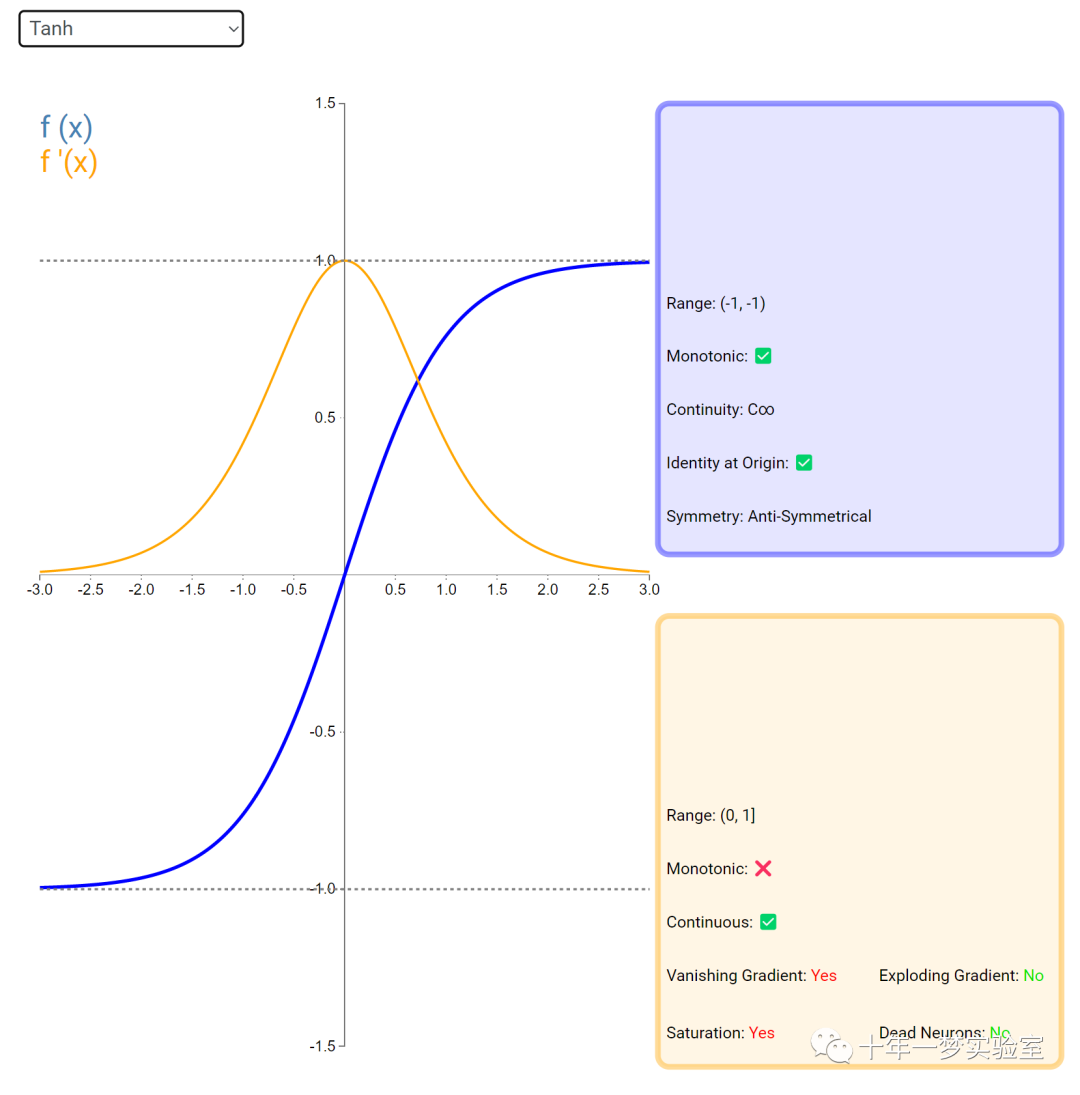
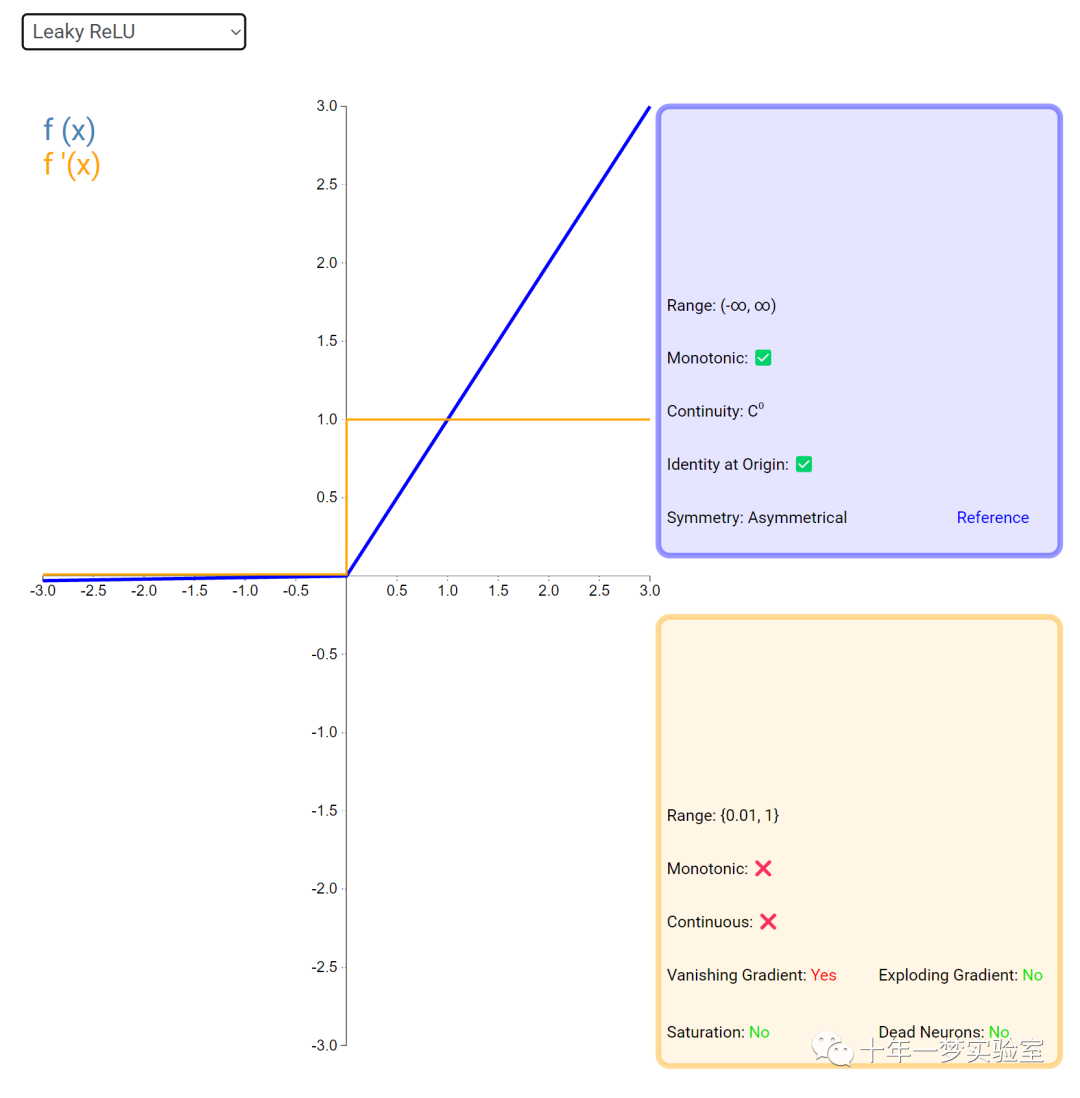
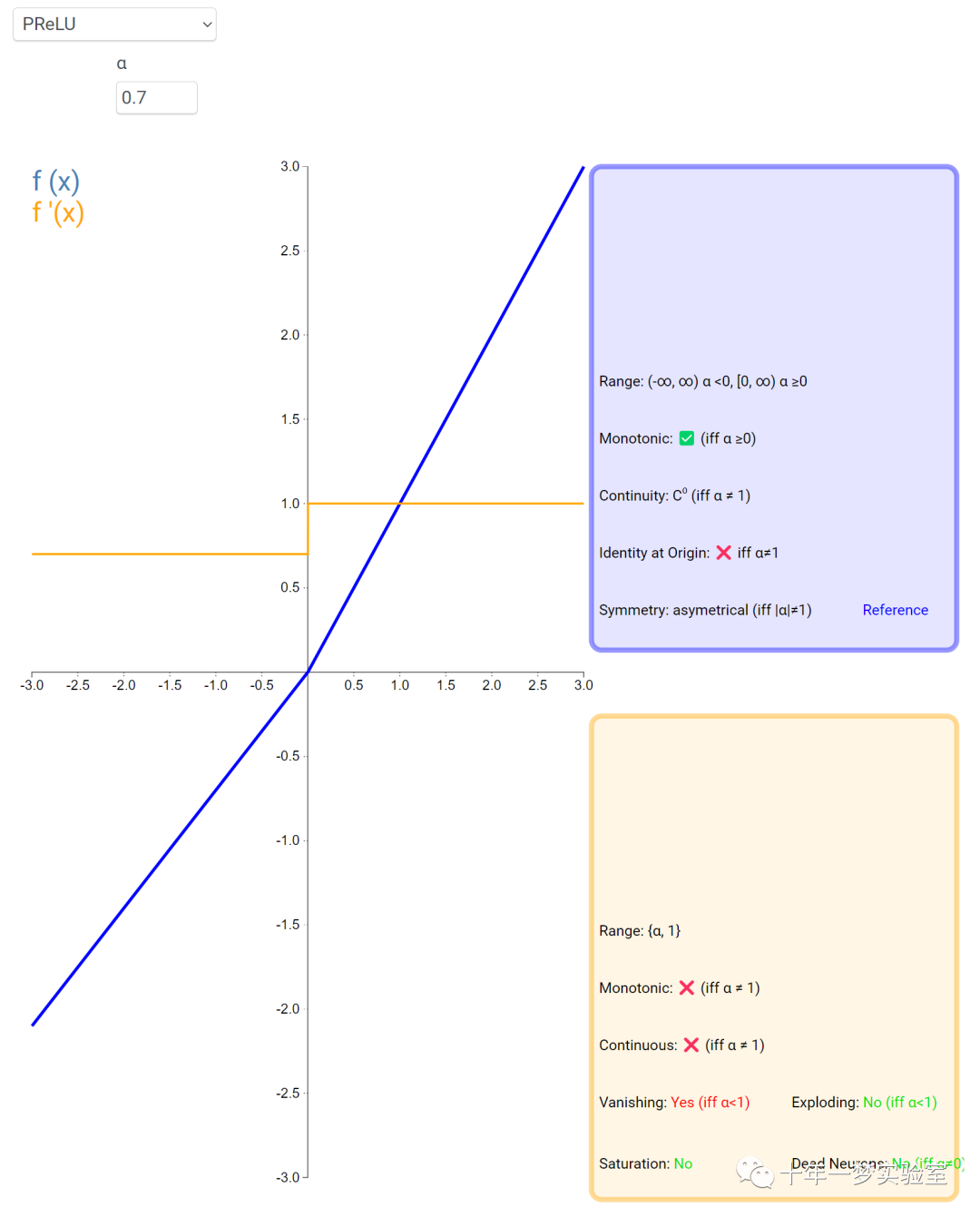
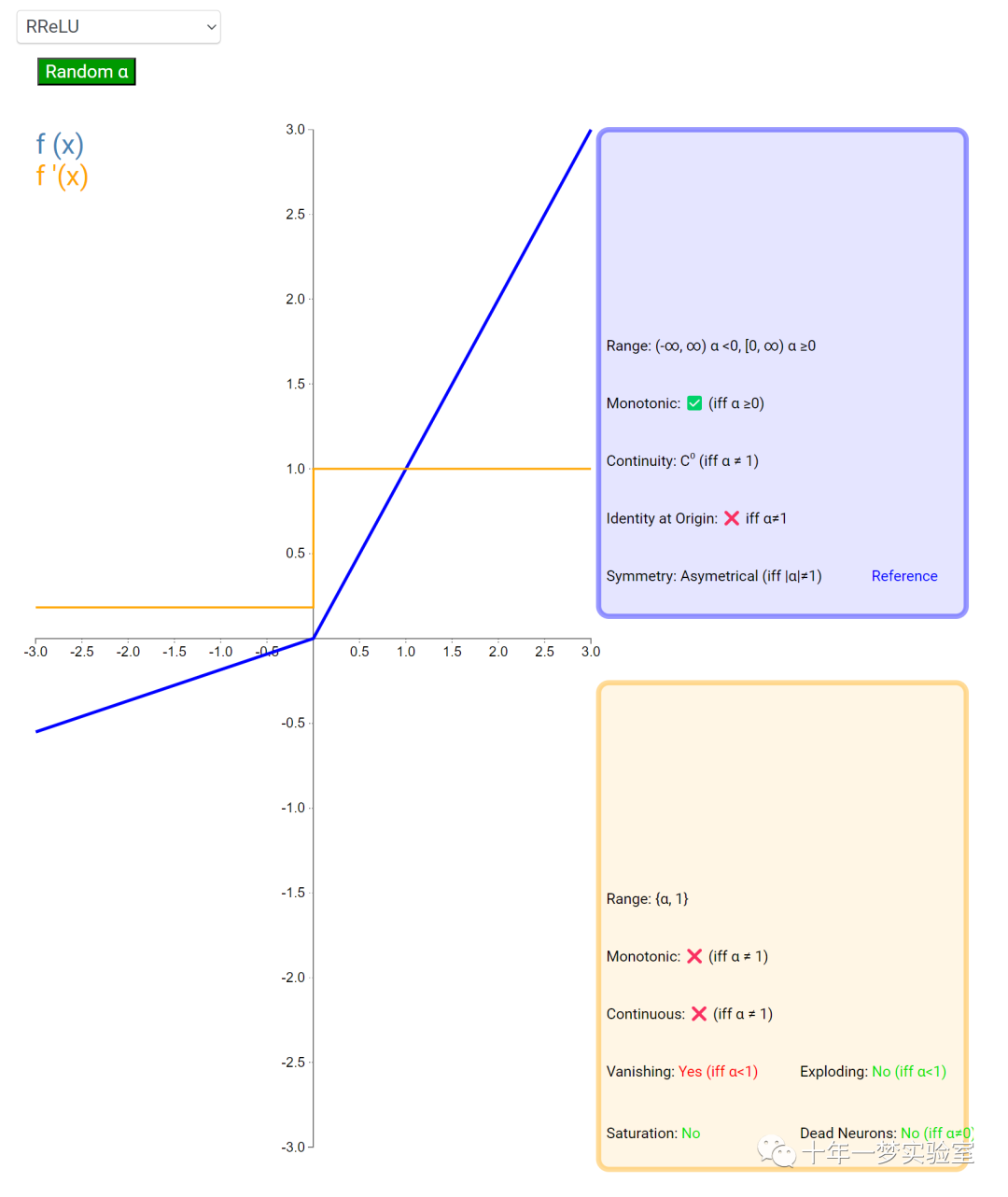
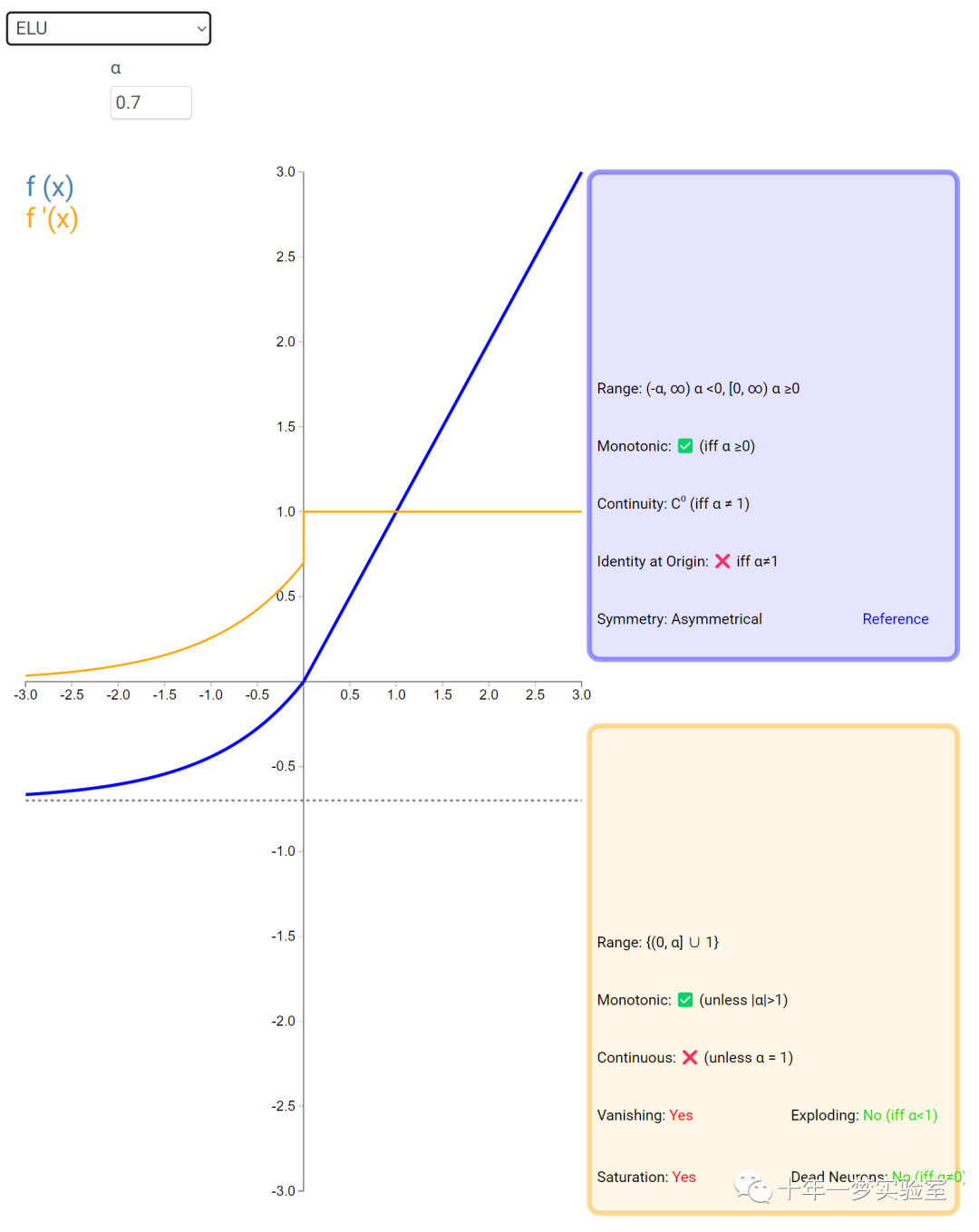
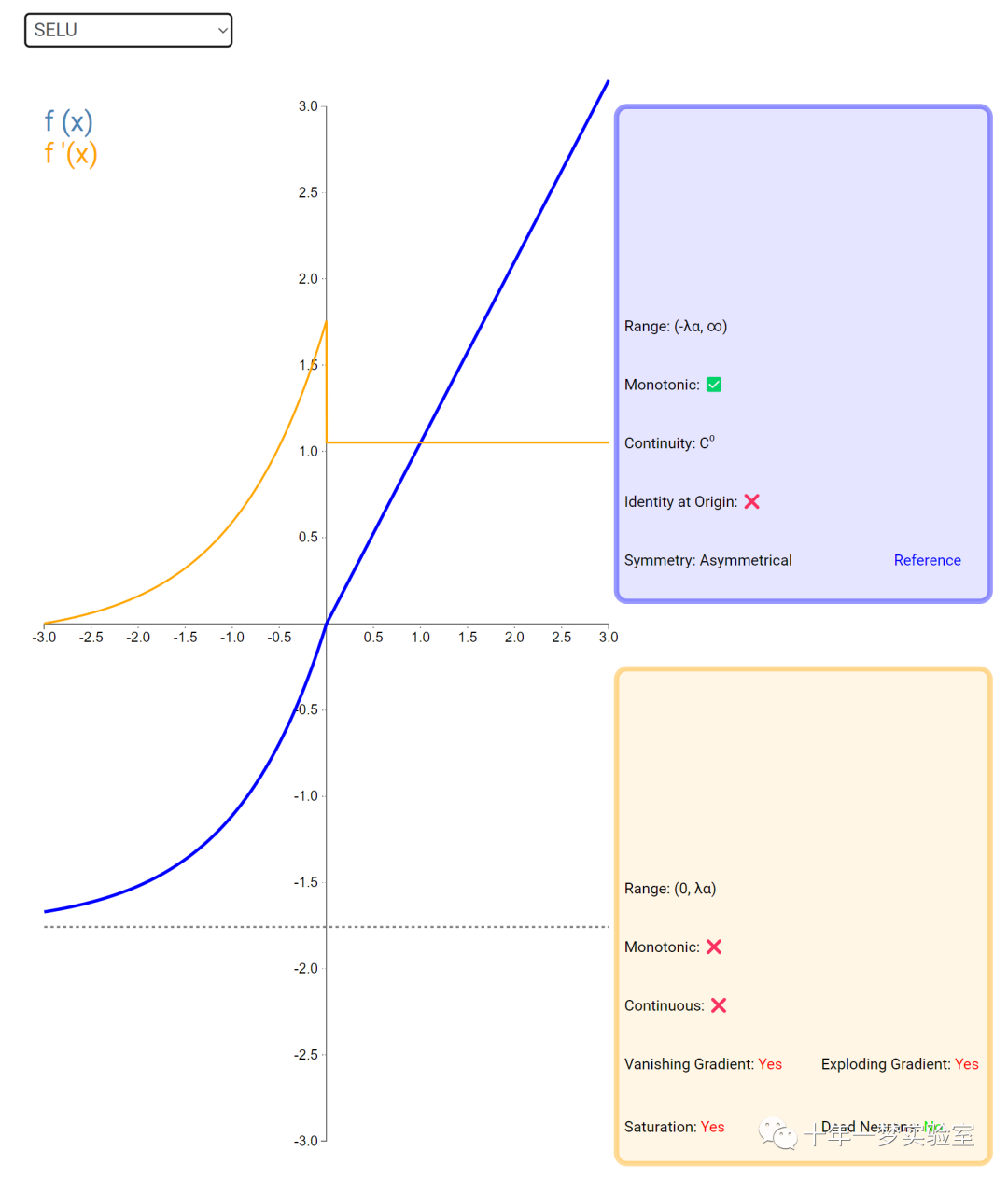
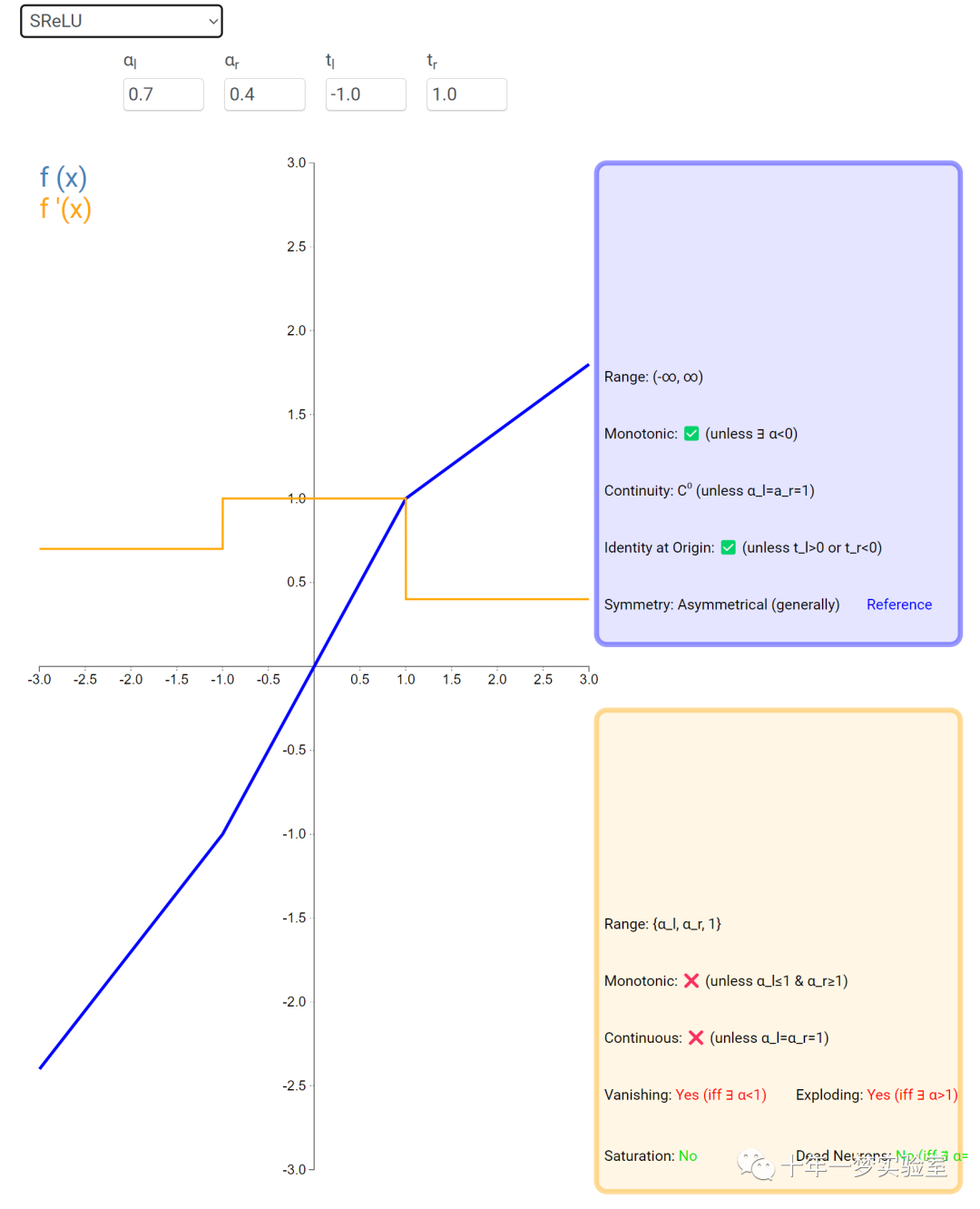
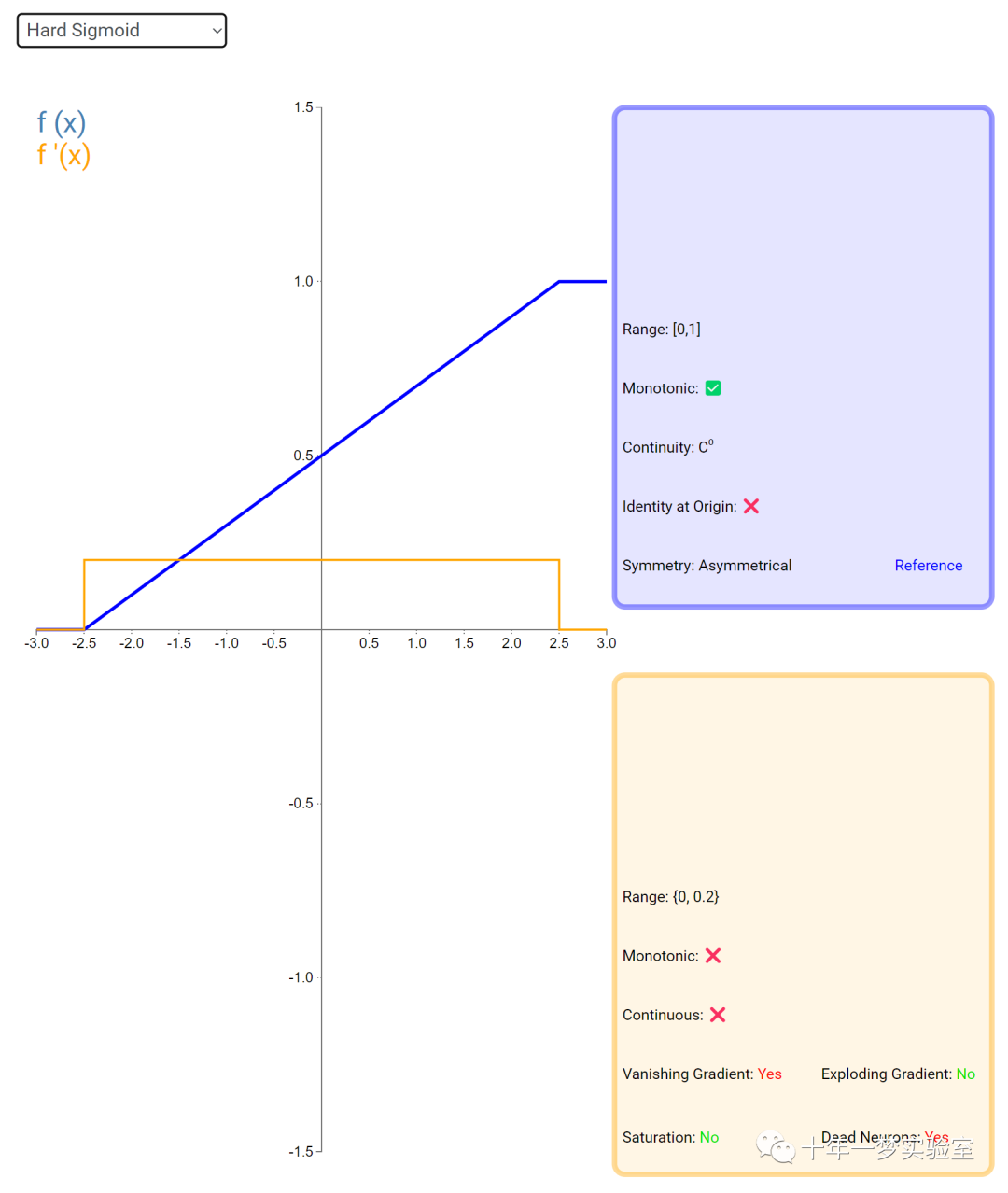
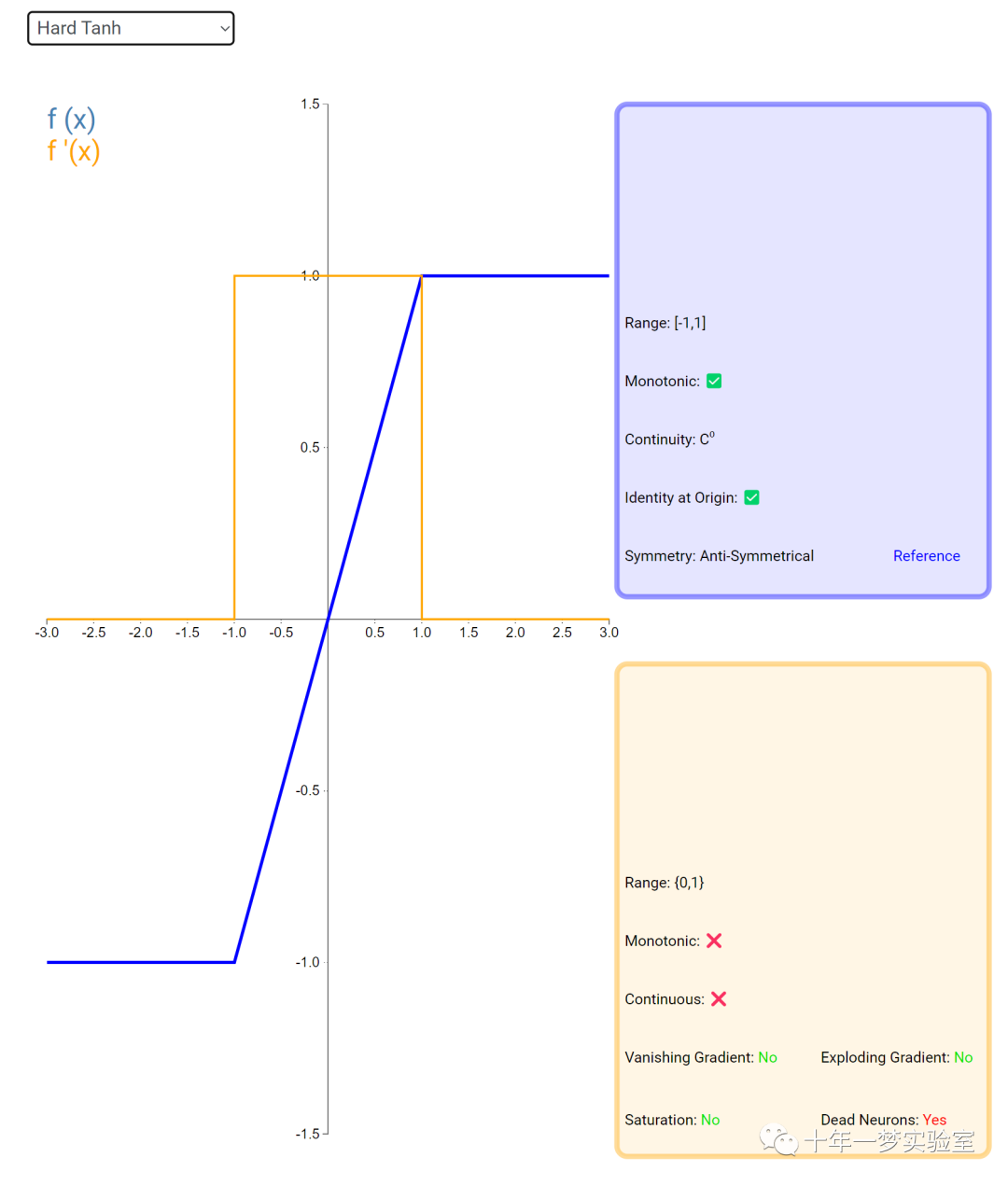
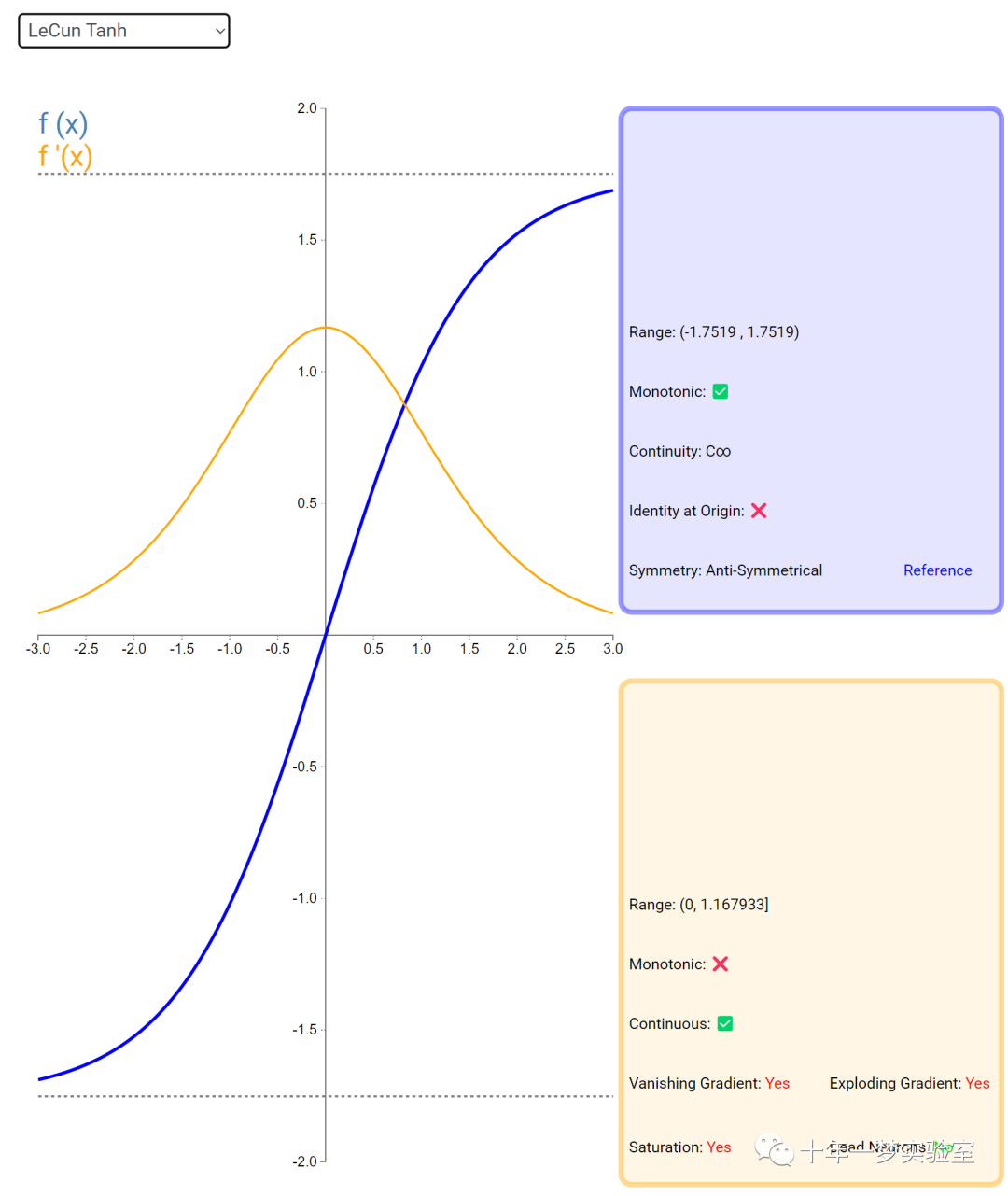
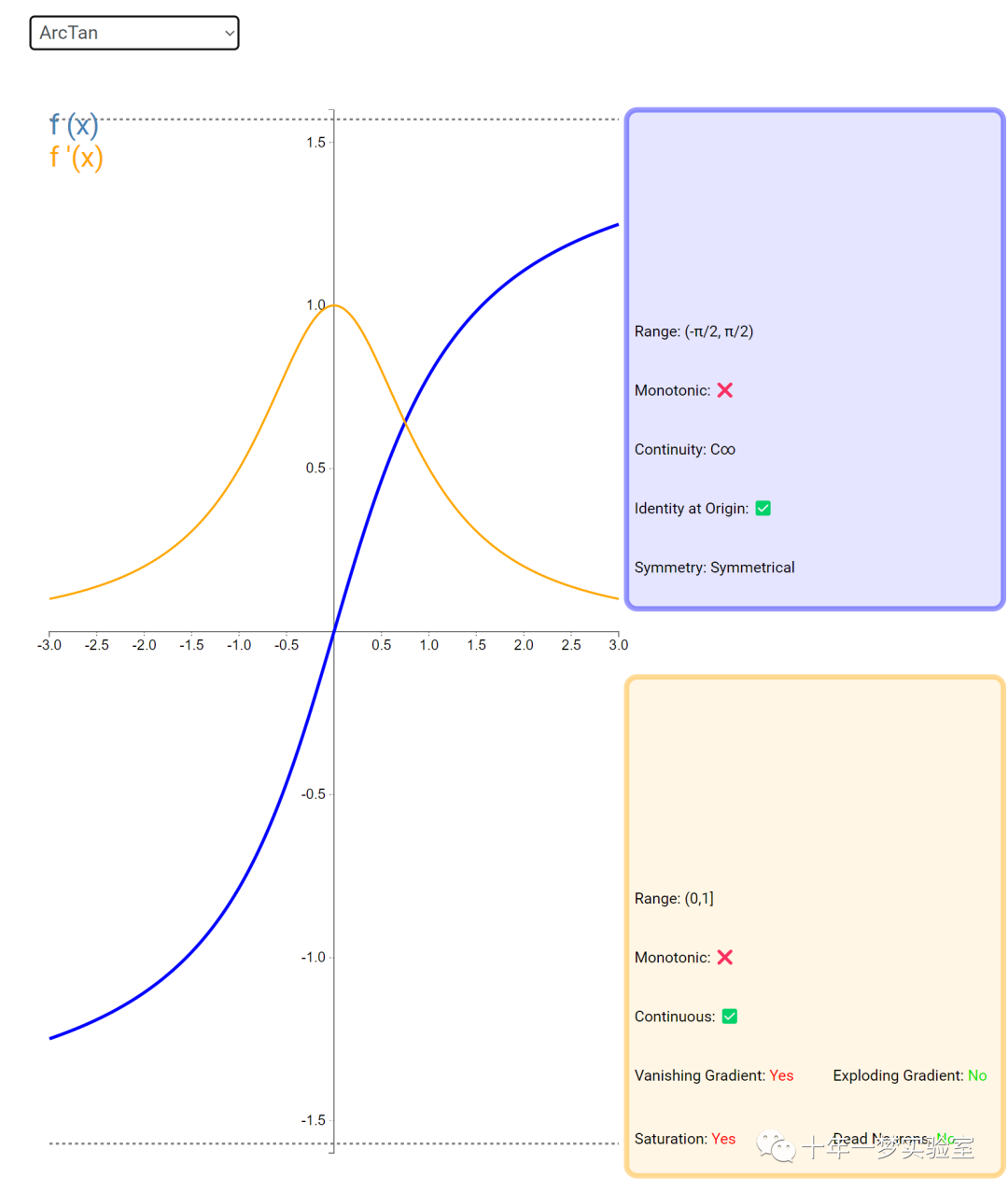
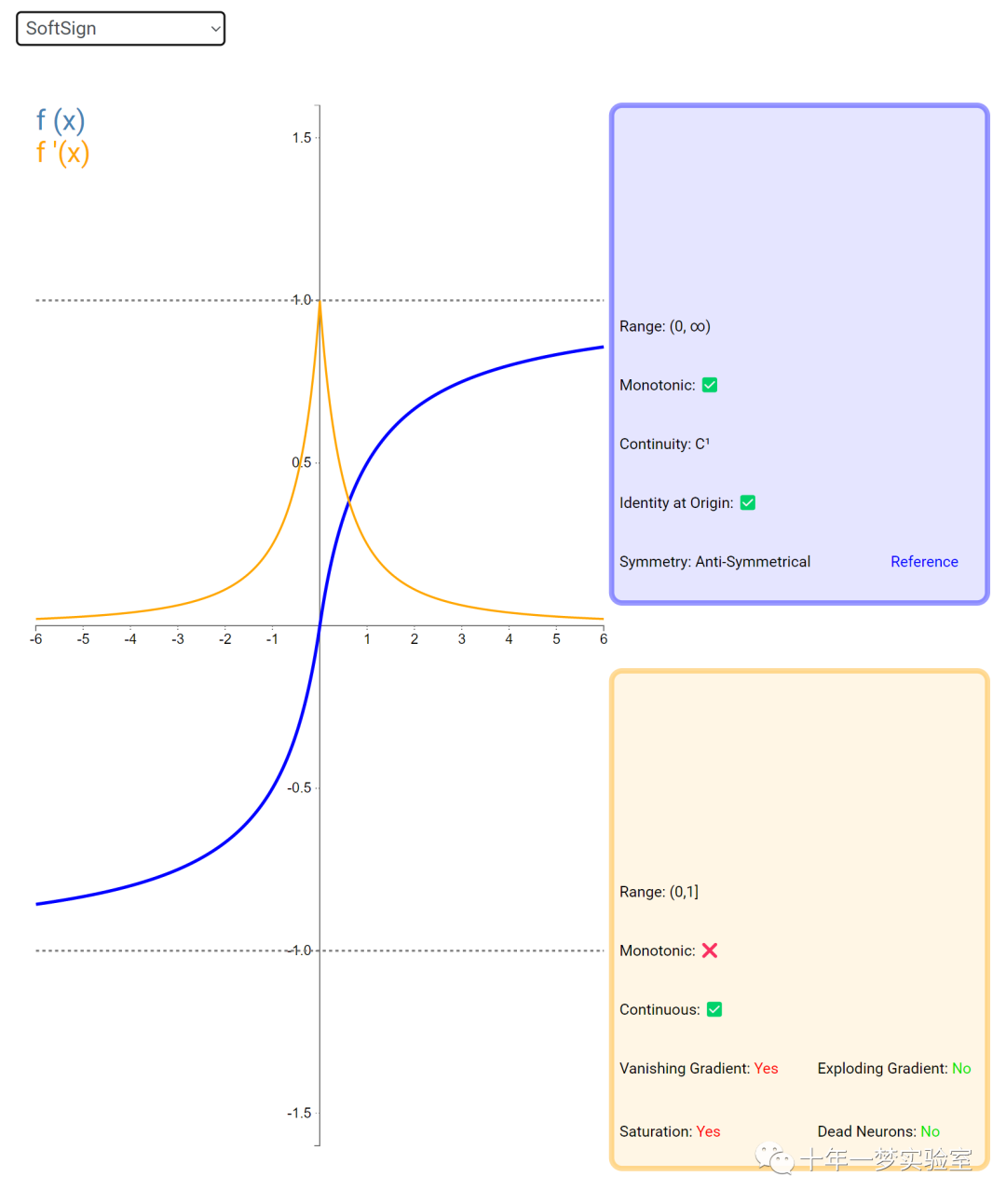
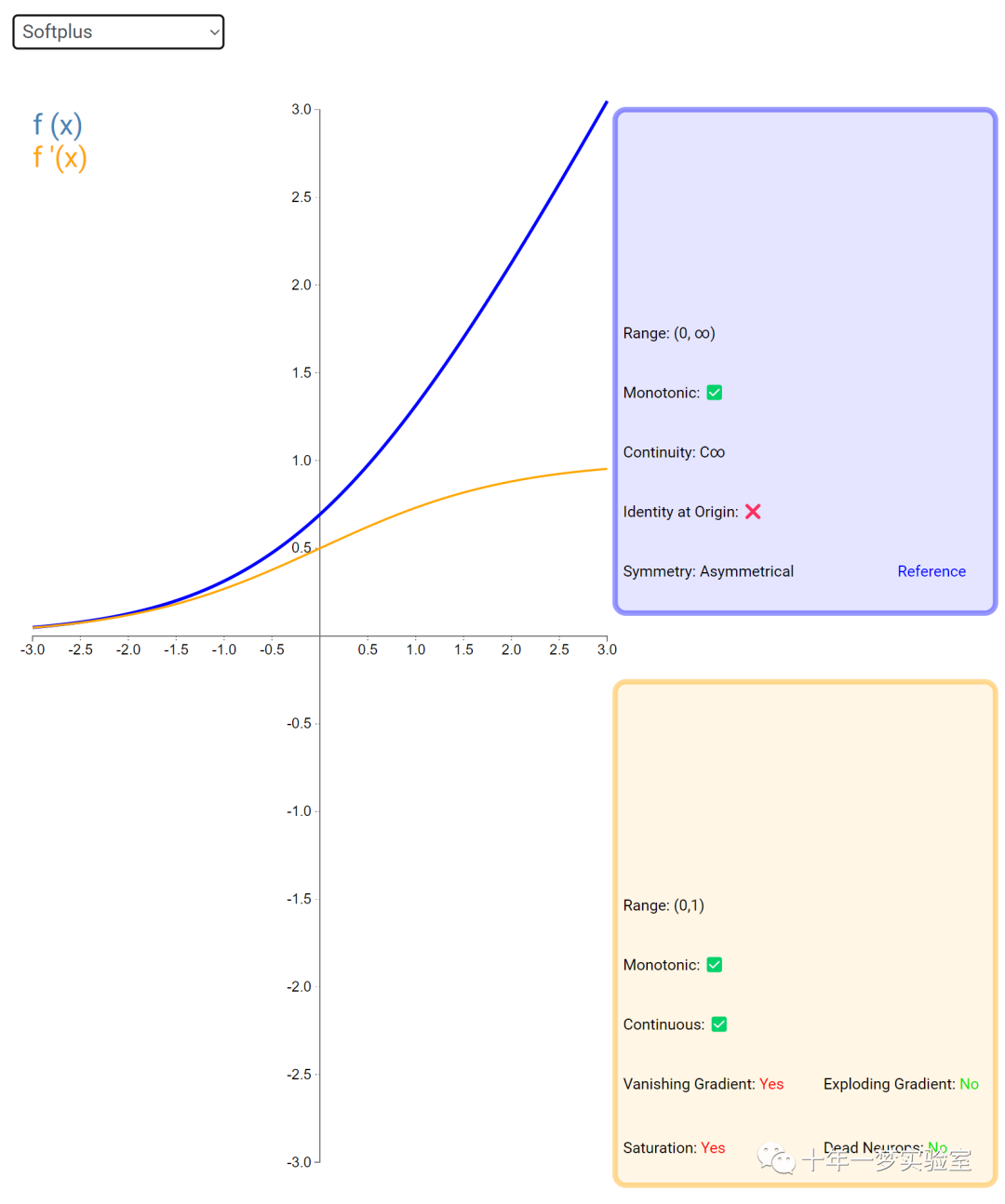
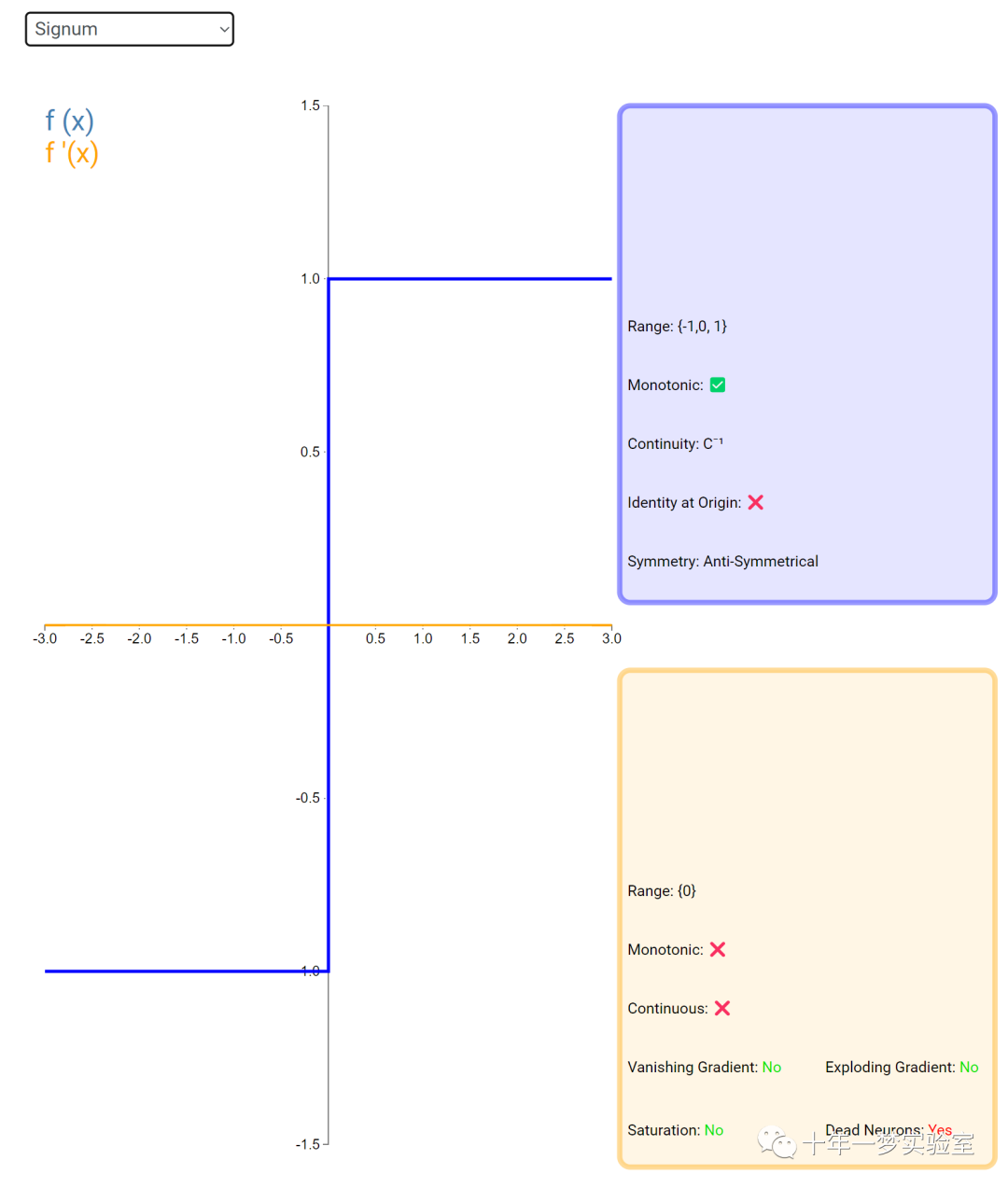
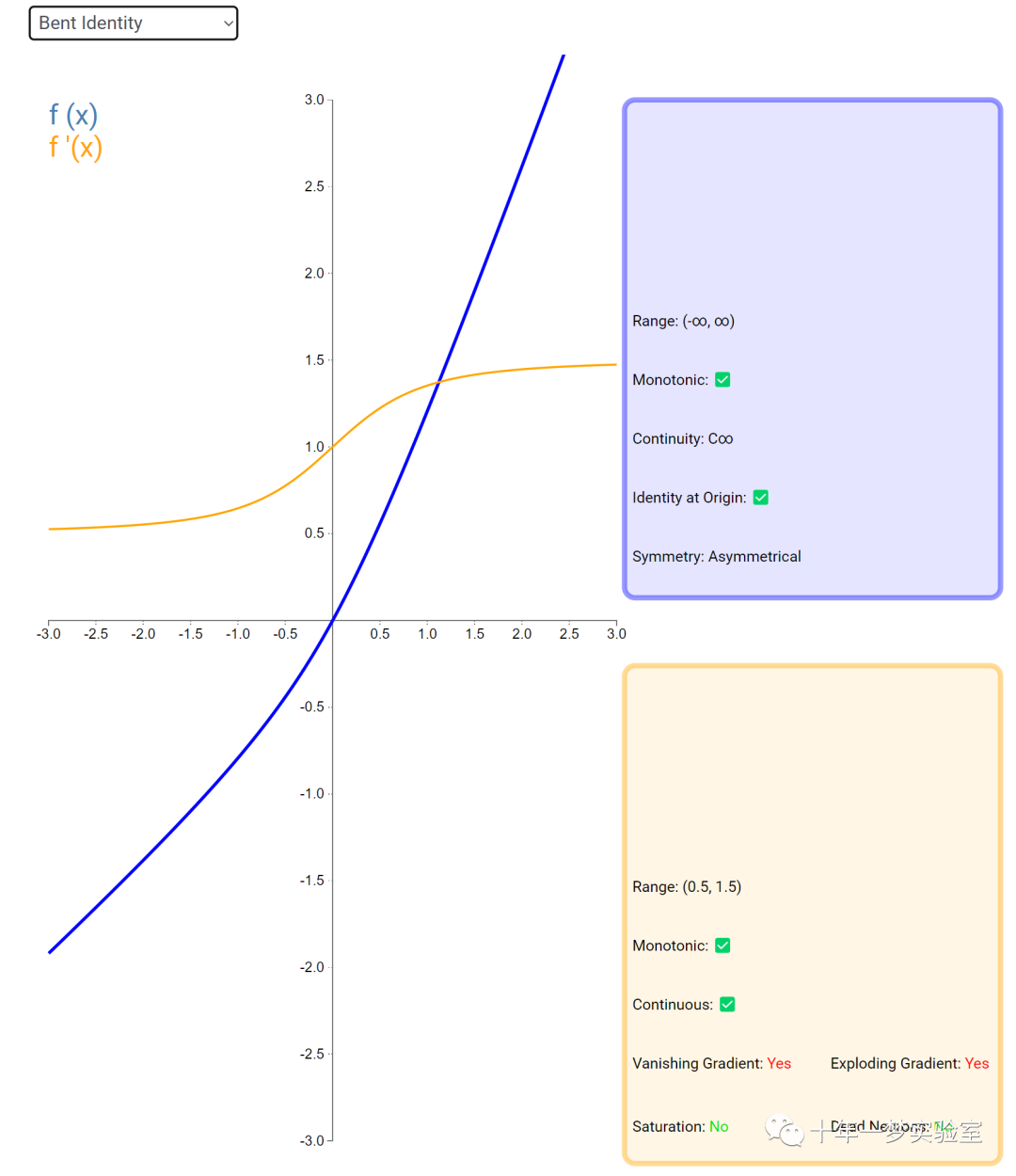
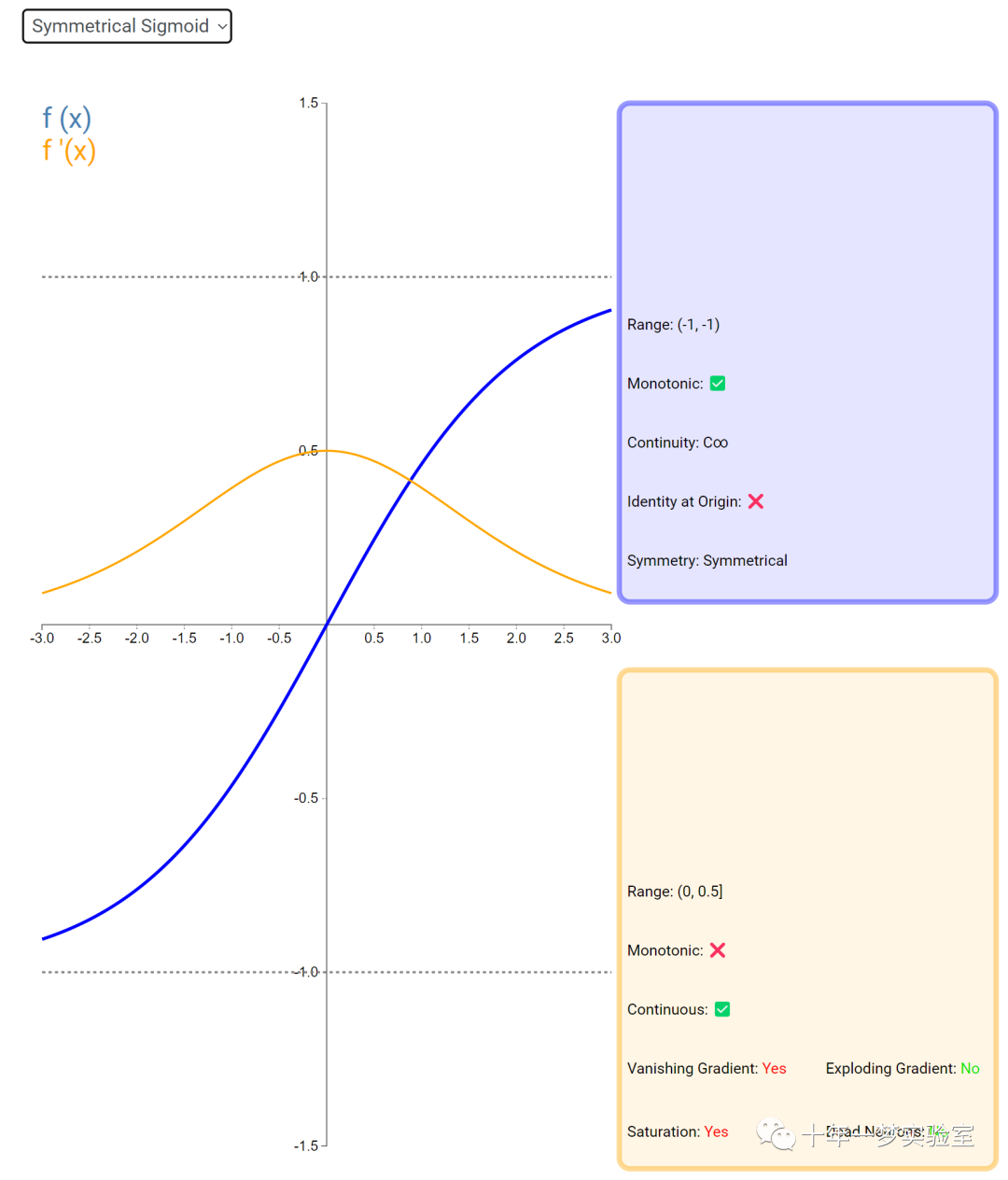
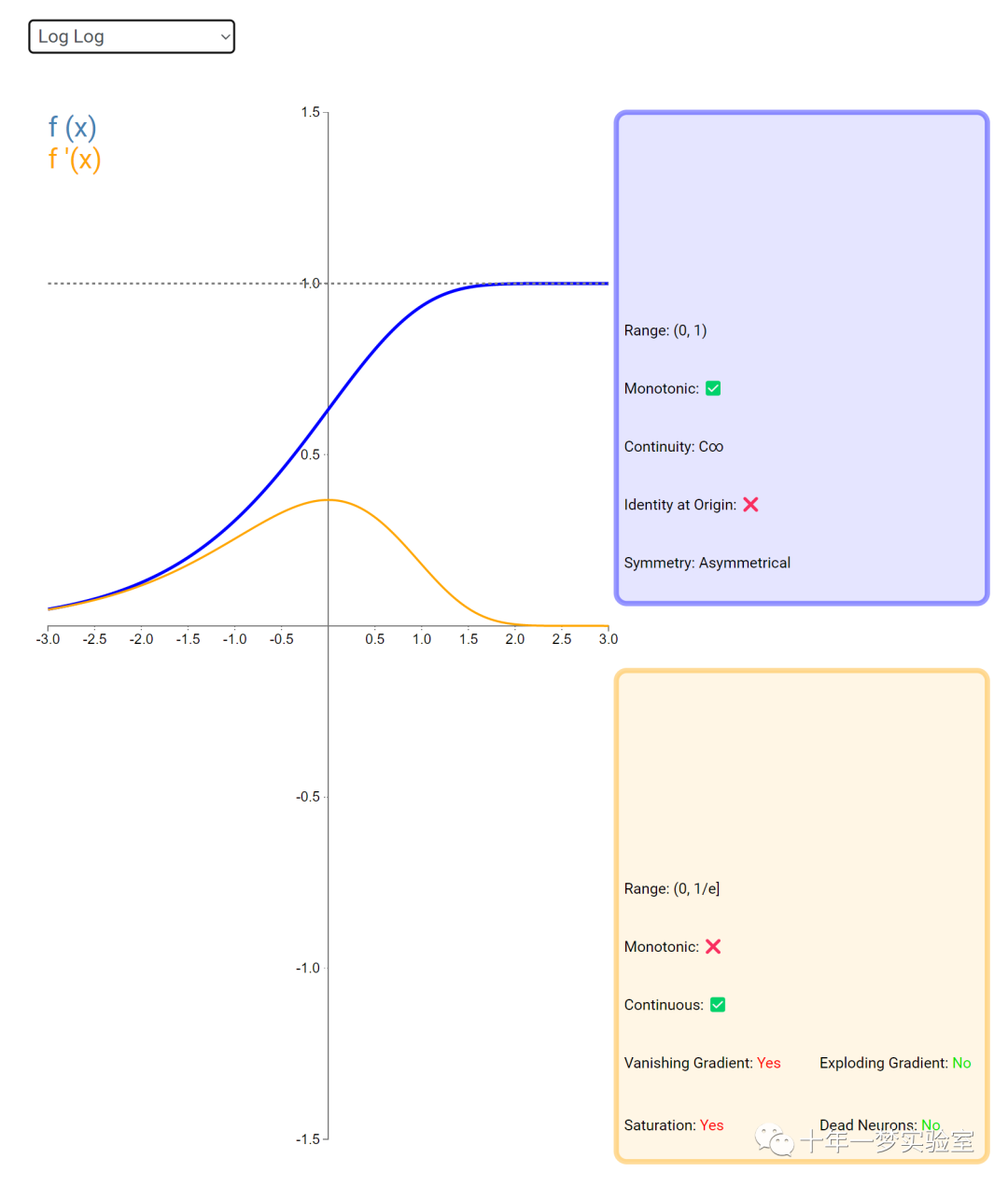
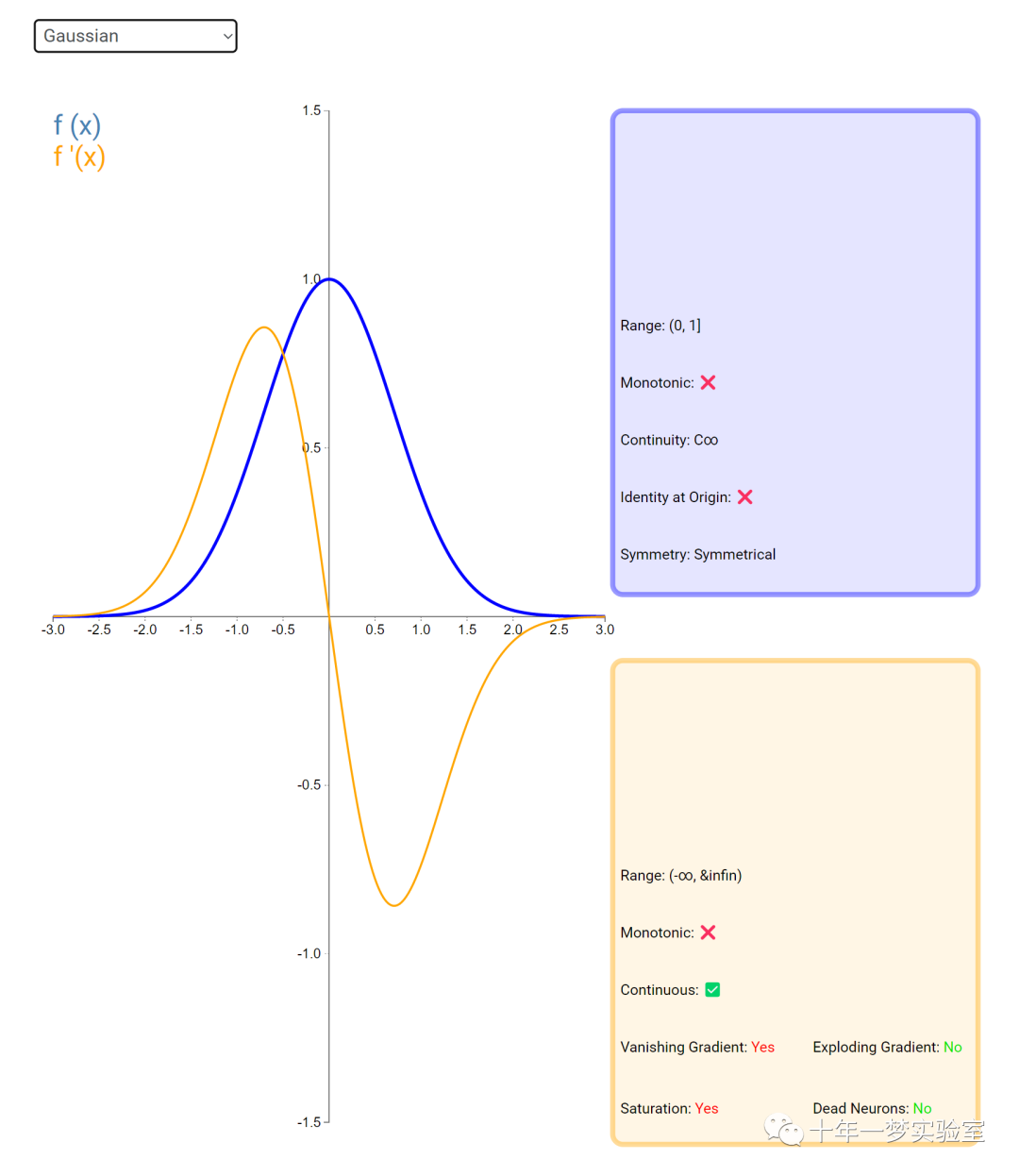
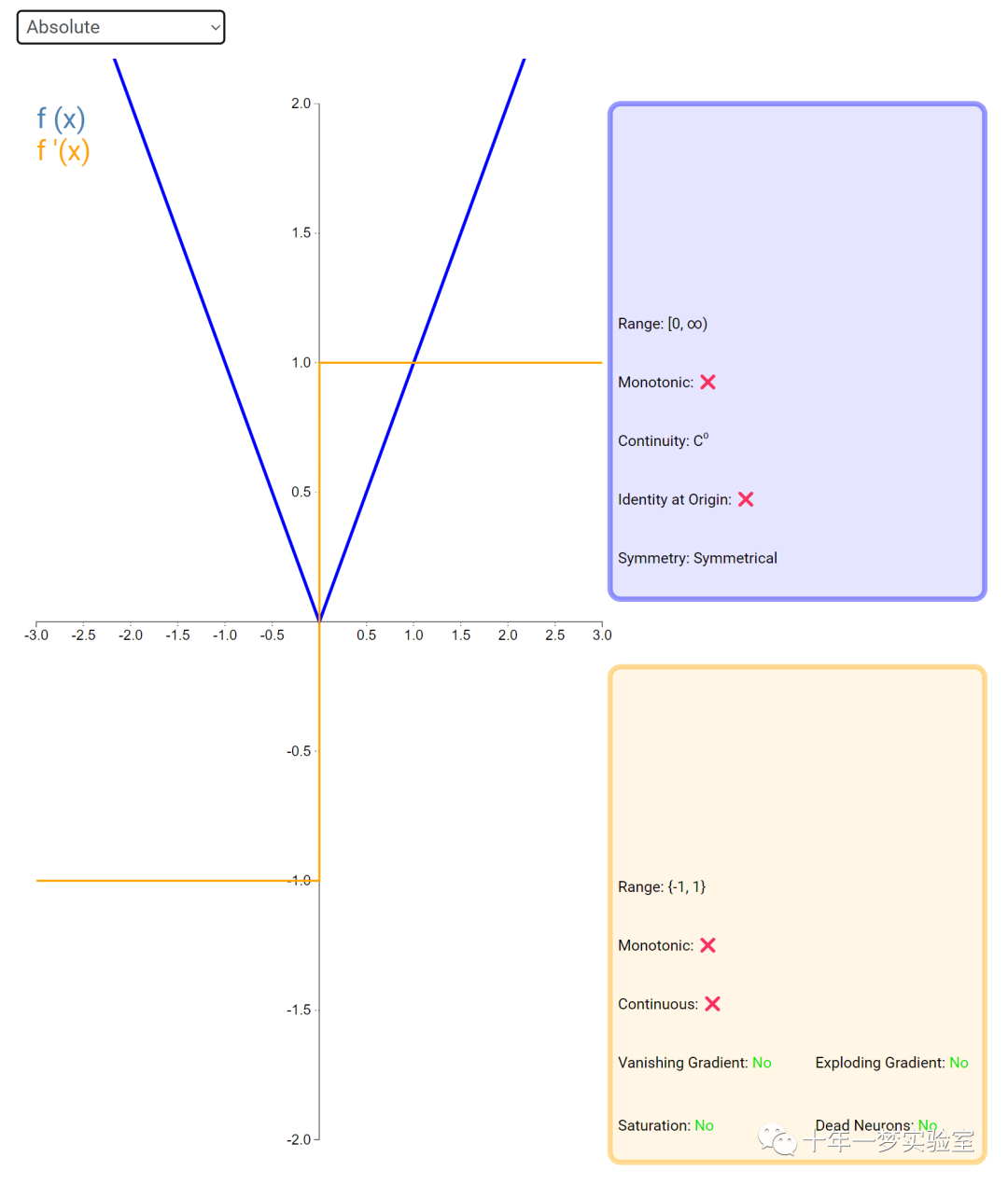
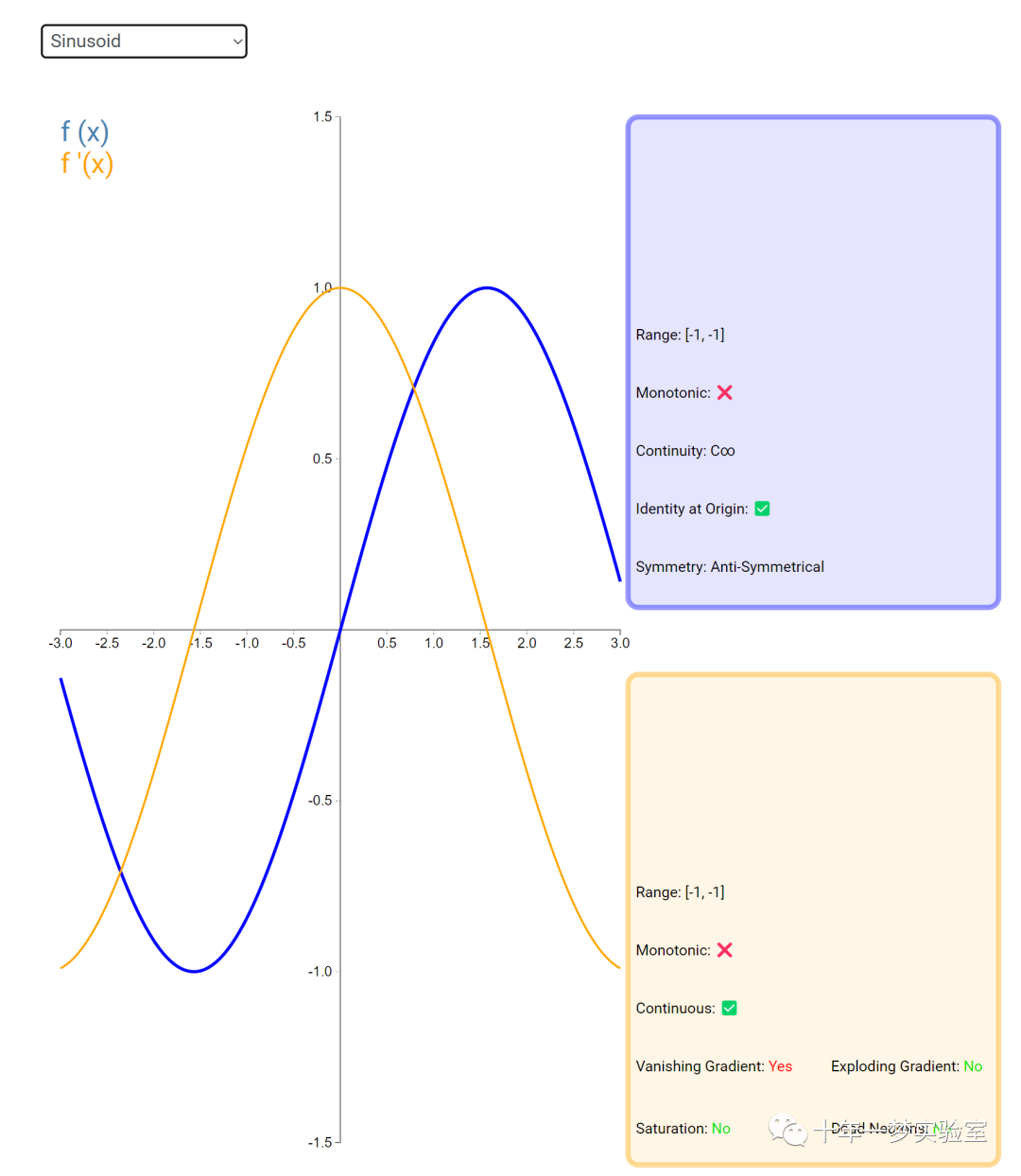
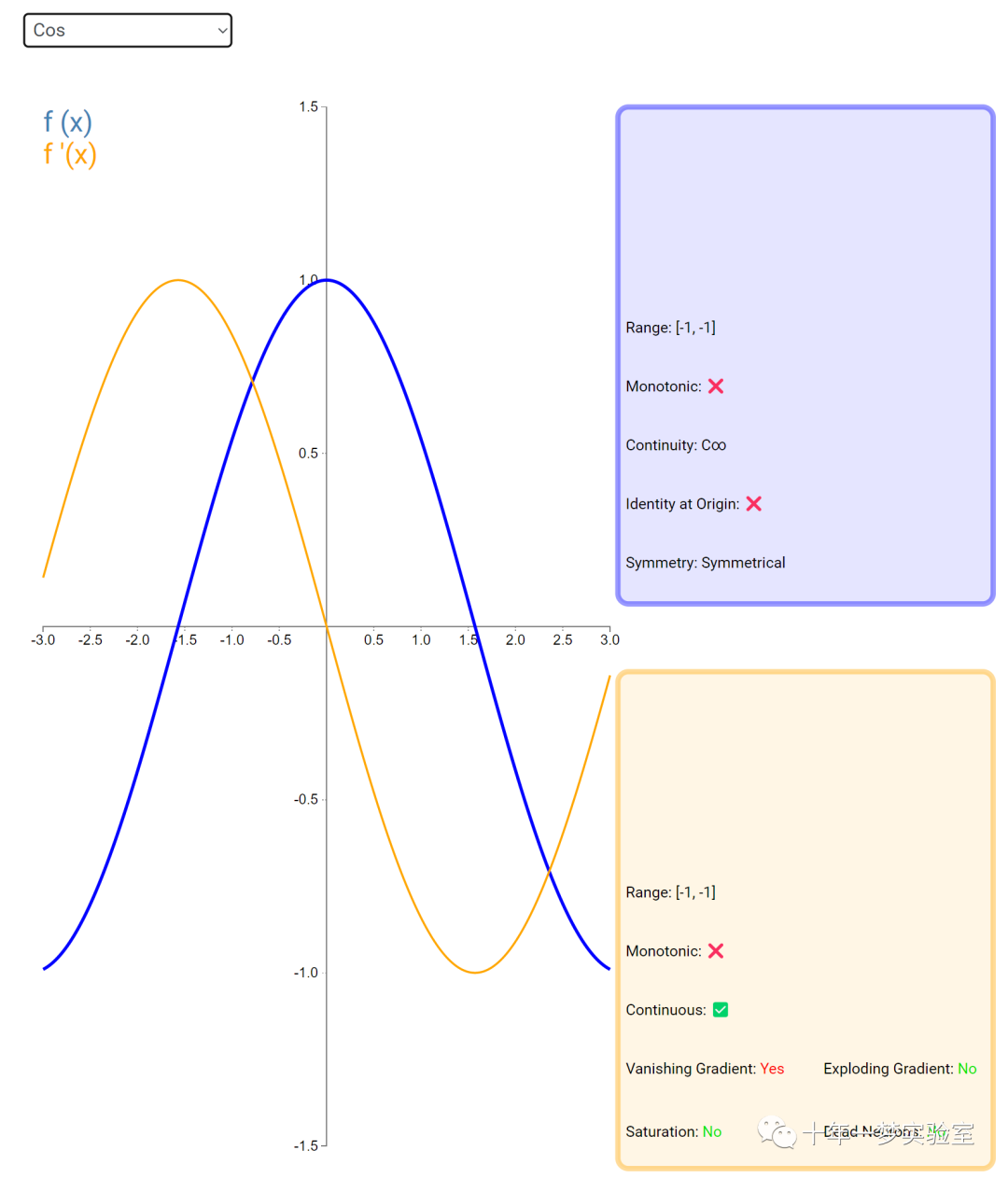
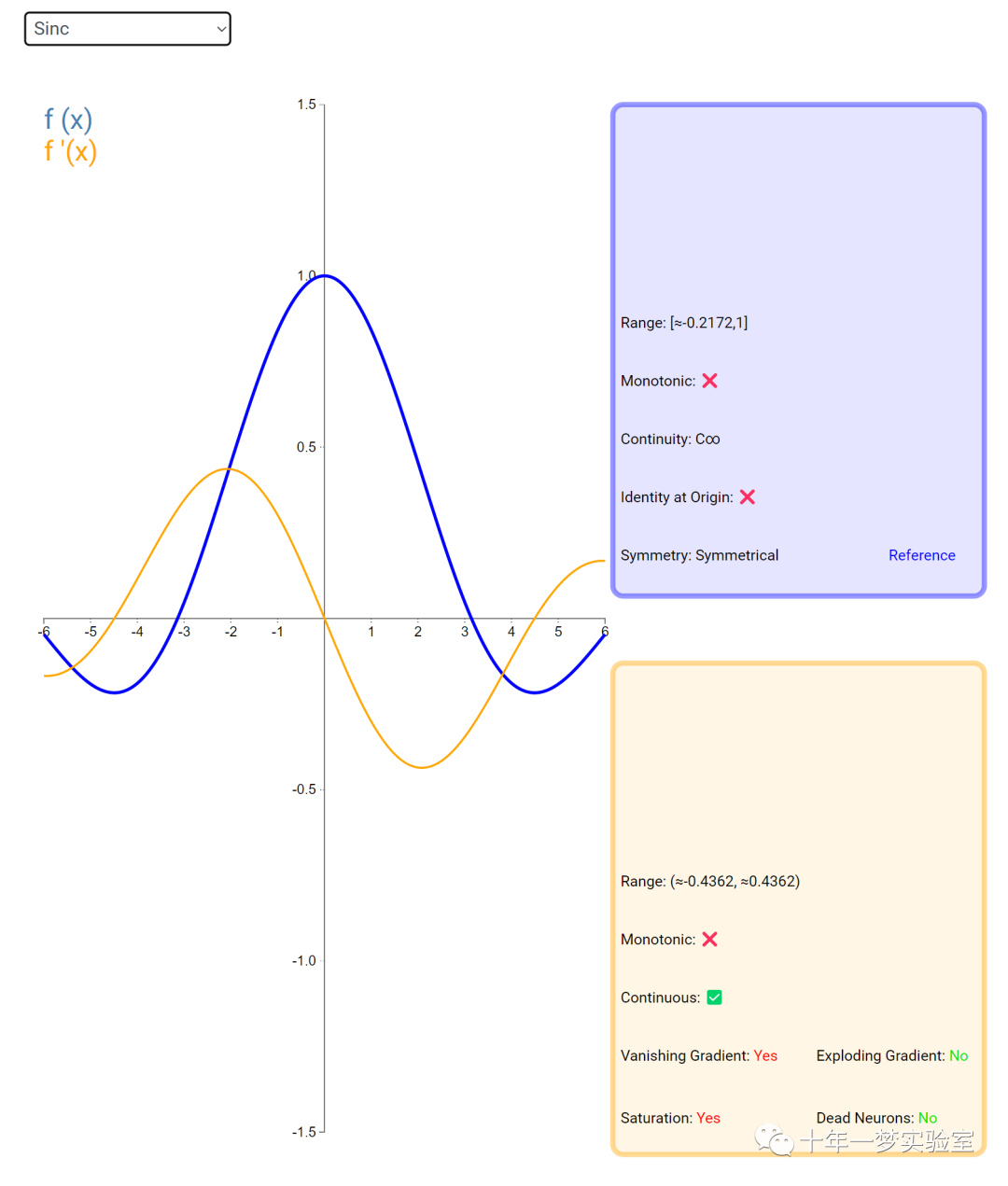
在神经网络中,激活函数通常是将向量中的每个元素独立地映射到一个新的值。这种映射是逐元素(element-wise)的,也就是说,每个元素的新值只取决于该元素的原值。
例如,ReLU(Rectified Linear Unit)激活函数就是一个常见的逐元素映射。它将输入向量中的每个元素x映射到max(0, x),即如果x大于0,就保留x,否则就将x置为0。同样,Sigmoid激活函数也是一个逐元素映射。它将输入向量中的每个元素x映射到1 / (1 + exp(-x)),这样可以将x的值压缩到0和1之间。


6.3 内积层

反向传播是同时对多个样本进行计算的。
6.4 损失层

Multinomial Logistic Loss
Infogain Loss - a generalization of MultinomialLogisticLossLayer.
Softmax with Loss - computes the multinomial logistic loss of the softmax of its inputs. It's conceptually identical to a softmax layer followed by a multinomial logistic loss layer, but provides a more numerically stable gradient.
Sum-of-Squares / Euclidean - computes the sum of squares of differences of its two inputs,
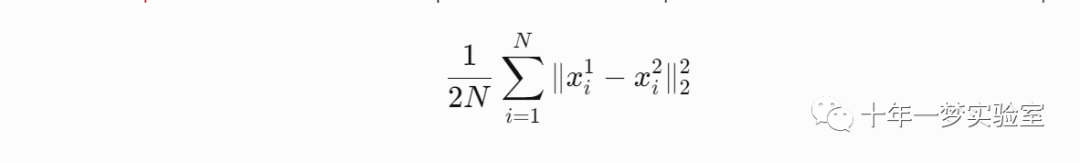
Hinge / Margin - The hinge loss layer computes a one-vs-all hinge (L1) or squared hinge loss (L2).
Sigmoid Cross-Entropy Loss - computes the cross-entropy (logistic) loss, often used for predicting targets interpreted as probabilities.
Accuracy / Top-k layer - scores the output as an accuracy with respect to target -- it is not actually a loss and has no backward step.
Contrastive Loss


caffe支持的各种损失函数都适用于哪些场景

6.5 求解器

Caffe 求解器支持哪些优化算法
Stochastic Gradient Descent (type: "SGD"),
AdaDelta (type: "AdaDelta"),
Adaptive Gradient (type: "AdaGrad"),
Adam (type: "Adam"),
Nesterov’s Accelerated Gradient (type: "Nesterov") and
RMSprop (type: "RMSProp")

详细介绍caffe支持的优化算法:
回答A

回答B

回答C

caffe支持的优化算法分别适用于哪些场景


神经网络的优化中一般使用梯度下降法,而不使用牛顿法这样的二阶优化技术的原因是什么?


分析参数初始化和动量项对算法的收敛行的影响


caffe支持的学习率计算策略

学习率是优化算法中的一个重要的超参数,它决定了每次更新权重的步长。学习率的大小会影响优化的速度和效果,一般来说,学习率不能太大,否则会导致优化不稳定或者发散,也不能太小,否则会导致优化过慢或者停滞。因此,合适的学习率计算策略是优化算法的关键。
Caffe 支持以下几种学习率计算策略:
固定(fixed):这是最简单的学习率计算策略,它使用一个固定的学习率,不随着迭代的进行而改变。这种策略适用于那些目标函数比较平滑,不需要动态调整学习率的情况。
步长(step):这是一种常用的学习率计算策略,它根据一个预设的步长,每隔一定的迭代次数,就将学习率乘以一个衰减因子。这种策略适用于那些目标函数比较复杂,需要逐渐降低学习率的情况。
指数(exp):这是一种较为灵活的学习率计算策略,它根据一个预设的指数,每次迭代,就将学习率乘以一个衰减因子的指数。这种策略适用于那些目标函数比较陡峭,需要快速降低学习率的情况。
逆时针(inv):这是一种较为稳定的学习率计算策略,它根据一个预设的幂,每次迭代,就将学习率除以一个增长因子的幂。这种策略适用于那些目标函数比较平缓,需要缓慢降低学习率的情况。
多项式(poly):这是一种较为精确的学习率计算策略,它根据一个预设的幂,每次迭代,就将学习率乘以一个多项式函数的值。这种策略适用于那些目标函数比较复杂,需要根据迭代的进度调整学习率的情况。
S型(sigmoid):这是一种较为平滑的学习率计算策略,它根据一个预设的幂,每次迭代,就将学习率乘以一个 S 型函数的值。这种策略适用于那些目标函数比较复杂,需要在初始阶段快速降低学习率,然后在后期阶段缓慢降低学习率的情况。
参考网址:
https://dashee87.github.io/deep%20learning/visualising-activation-functions-in-neural-networks/ Visualising Activation Functions in Neural Networks - dashee87.github.io
https://caffe.berkeleyvision.org/tutorial/layers.html Caffe | Layer Catalogue --- Caffe | 层目录 (berkeleyvision.org)
https://caffe2.ai/docs/caffe-migration.html What is Caffe2? | Caffe2
https://github.com/pytorch/pytorch pytorch/pytorch: Tensors and Dynamic neural networks in Python with strong GPU acceleration (github.com)
https://github.com/pytorch/examples
https://blog.csdn.net/lliming2006/article/details/76636329
http://caffe.berkeleyvision.org/doxygen/namespacecaffe.html Caffe中的损失函数_caffe设置损失函数-CSDN博客
https://cloud.tencent.com/developer/article/1670389 caffe详解之损失函数-腾讯云开发者社区-腾讯云 (tencent.com)
https://blog.csdn.net/wuqingshan2010/article/details/71156236 Caffe中求解器(Solver)介绍_solver.compute-CSDN博客
https://zhuanlan.zhihu.com/p/24087905 Caffe入门与实践-简介 - 知乎 (zhihu.com)
https://caffe.berkeleyvision.org/tutorial/solver.html 求解器
The End
正传播向传播的规律