目录
1.课题概述
2.系统仿真结果
3.核心程序与模型
4.系统原理简介
4.1 PMSM数学模型
4.2 矢量控制策略
4.3 PI控制器设计
4.4 控制系统实现
5.完整工程文件
1.课题概述
基于PI控制的PMSM永磁同步电机控制系统simulink建模与仿真。其中,基于PI(比例-积分)控制器的矢量控制策略因其简单、可靠的特点而被广泛采用。永磁同步电机采用建模方式实现,不使用simulink的自带模型。
2.系统仿真结果
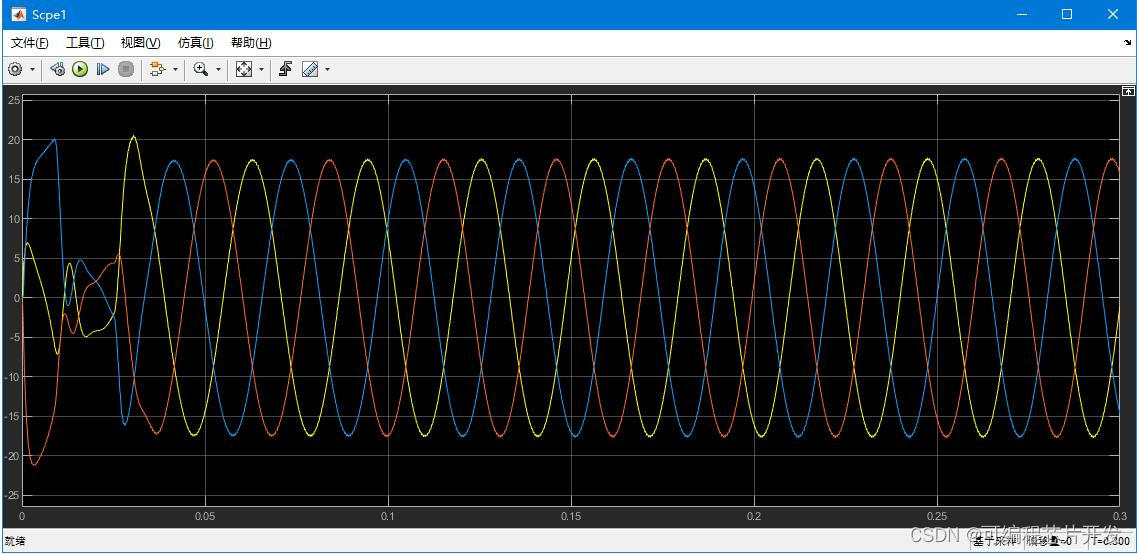

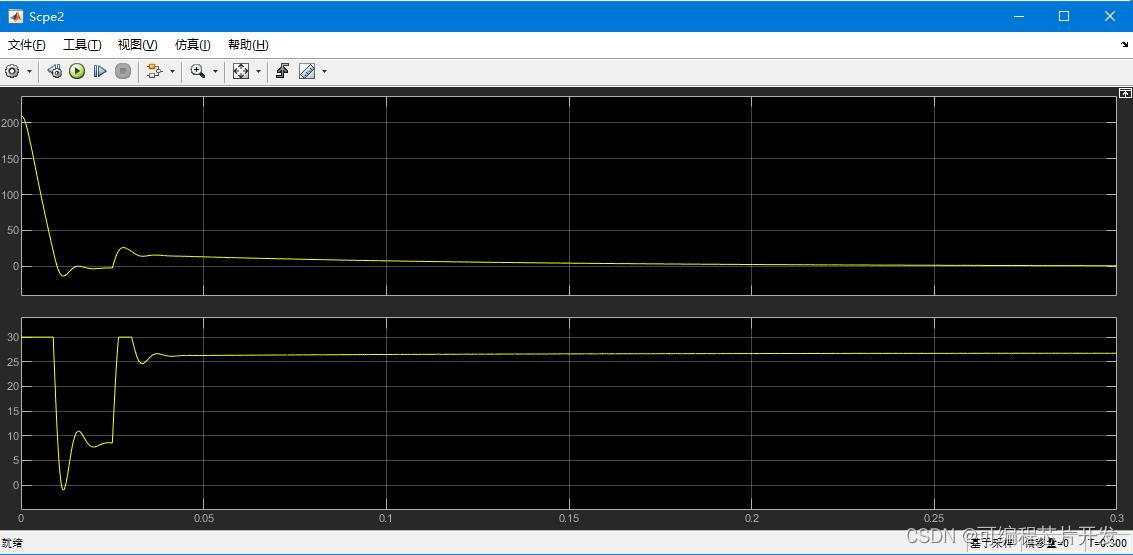
3.核心程序与模型
版本:MATLAB2022a

17
4.系统原理简介
永磁同步电机(PMSM)因其高效率、高功率因数、高转矩密度等优点在诸多领域得到广泛应用。为了实现PMSM的高性能控制,需要采用先进的控制策略。其中,基于PI(比例-积分)控制器的矢量控制策略因其简单、可靠的特点而被广泛采用。本文将详细介绍基于PI控制的PMSM控制系统的原理。
4.1 PMSM数学模型
由于电机定转子存在相对运动,气隙磁密存在谐波,导致电磁关系复杂;若再考虑电流谐波,磁路饱和,以及电导、磁导等参数摄动,系统复杂程度将进一步提高。为简化分析,便于建模和设计对应的控制策略,往往对PMSM作出以下假设:
1)三相绕组对称,空间互差2π/3电角度;
2)忽略磁路饱和;
3)不计磁滞损耗和涡流损耗;
4)忽略齿槽效应,每相磁动势沿气隙正弦分布;
5)转子无阻尼绕组。
因此,PMSM在三相静止a-b-c,a-b-c,a−b−c坐标系下的电压方程和磁链方程可建立为:
4.2 矢量控制策略
矢量控制策略通过坐标变换将PMSM的定子电流分解为相互正交的励磁分量和转矩分量,并分别进行控制。这样可以实现对PMSM的解耦控制,提高控制性能。在矢量控制中,通常采用id=0的控制方式,即直轴电流为零,此时电磁转矩与交轴电流成正比,简化了控制系统。
4.3 PI控制器设计
PI控制器是一种线性控制器,其传递函数可表示为:
(G(s) = K_p + \frac{K_i}{s})
其中,(K_p)为比例系数;(K_i)为积分系数。PI控制器通过对误差信号的比例和积分作用来消除稳态误差,提高系统的动态响应性能。
在PMSM控制系统中,通常需要设计两个PI控制器,分别用于调节直轴电流和交轴电流。通过调整PI控制器的参数,可以实现对PMSM的快速、准确控制。
4.4 控制系统实现
基于PI控制的PMSM控制系统实现过程如下:
采集PMSM的定子电流和转子位置信号;
通过坐标变换将定子电流从abc坐标系变换到dq坐标系;
设计PI控制器,并根据给定的直轴和交轴电流参考值计算PI控制器的输出;
将PI控制器的输出作为PWM调制信号的输入,生成PWM波形;
将PWM波形作用于PMSM的逆变器,驱动PMSM运转;
重复以上步骤,实现闭环控制。
5.完整工程文件
v