前言

💫你好，我是辰chen，本文旨在准备考研复试或就业
💫本文内容来自某机构网课，是我为复试准备的第一个项目
💫欢迎大家的关注，我的博客主要关注于考研408以及AIoT的内容
🌟 预置知识详见我的AIoT板块，需掌握 基本Python语法, Numpy, Pandas, Matplotlib

以下的几个专栏是本人比较满意的专栏(大部分专栏仍在持续更新)，欢迎大家的关注：

💥ACM-ICPC算法汇总【基础篇】
💥ACM-ICPC算法汇总【提高篇】
💥AIoT(人工智能+物联网)
💥考研
💥CSP认证考试历年题解

最小二乘法的推导

注意这里定义的凹凸函数和考研中的凹凸函数的定义正好是相反的

使用正规方程求解 $y=wx+b$

import numpy as np
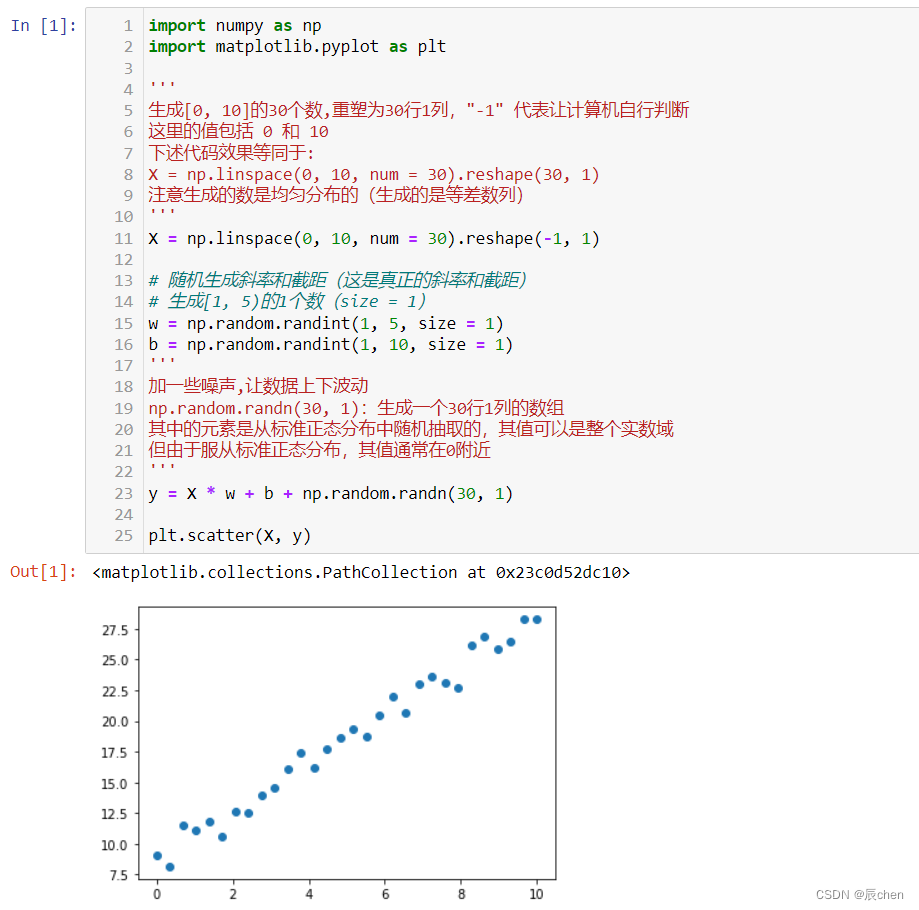
import matplotlib.pyplot as plt'''
生成[0, 10]的30个数,重塑为30行1列，"-1" 代表让计算机自行判断
这里的值包括 0 和 10
下述代码效果等同于:
X = np.linspace(0, 10, num = 30).reshape(30, 1)
注意生成的数是均匀分布的（生成的是等差数列）
'''
X = np.linspace(0, 10, num = 30).reshape(-1, 1)# 随机生成斜率和截距（这是真正的斜率和截距）
# 生成[1, 5)的1个数（size = 1）
w = np.random.randint(1, 5, size = 1)
b = np.random.randint(1, 10, size = 1)
'''
加一些噪声,让数据上下波动
np.random.randn(30, 1)：生成一个30行1列的数组
其中的元素是从标准正态分布中随机抽取的，其值可以是整个实数域
但由于服从标准正态分布，其值通常在0附近
'''
y = X * w + b + np.random.randn(30, 1)plt.scatter(X, y)

'''
根据最小二乘法去估计 w 和 b
再次强调上述的 w 和 b 是真实值，现求 w 和 b 的估计值
需要给X额外去添加一列全为1的列, axis = 1 代表列拼接
'''
X = np.concatenate([X, np.full(shape = (30, 1),fill_value= 1)],axis = 1)# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # 保留2位小数

print('一元一次方程真实的斜率和截距是：', w, b)
print('通过正规方程计算求解的斜率和截距是：', θ )'''
二维切片:
提取第一行:X[0, :]
提取第一列:X[:, 0]
提取最后一行:X[-1, :]
提取最后一列:X[:, -1]
提取第二行:X[1, :]
切片的语法是:array[start_row : stop_row, start_col : stop_col]
start_row 和 stop_row 分别表示行切片的起始和结束位置；
start_col 和 stop_col 分别表示列切片的起始和结束位置
'''plt.plot(X[:,0],X.dot(θ),color = 'green')'''
例子:
import numpy as nparr_2d = np.array([[0, 1, 2],[3, 4, 5],[6, 7, 8]])# 提取第一行
row_1 = arr_2d[0, :]
print(row_1)# 提取第一列
col_1 = arr_2d[:, 0]
print(col_1)# 提取子矩阵（2x2）
sub_matrix = arr_2d[1:3, 0:2]
print(sub_matrix)
''''''
输出:
print(row_1)：[0 1 2]
print(col_1)：[0 3 6]
print(sub_matrix)：[[3 4][6 7]]
'''

# 组合代码，同时打印出来两幅图
import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(0, 10, num = 30).reshape(-1, 1)
w = np.random.randint(1, 5, size = 1)
b = np.random.randint(1, 10, size = 1)
y = X * w + b + np.random.randn(30, 1)
plt.scatter(X, y)
X = np.concatenate([X, np.full(shape = (30, 1),fill_value= 1)],axis = 1)
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # 保留2位小数
print('一元一次方程真实的斜率和截距是：', w, b)
print('通过正规方程计算求解的斜率和截距是：', θ )
plt.plot(X[:,0],X.dot(θ),color = 'green')

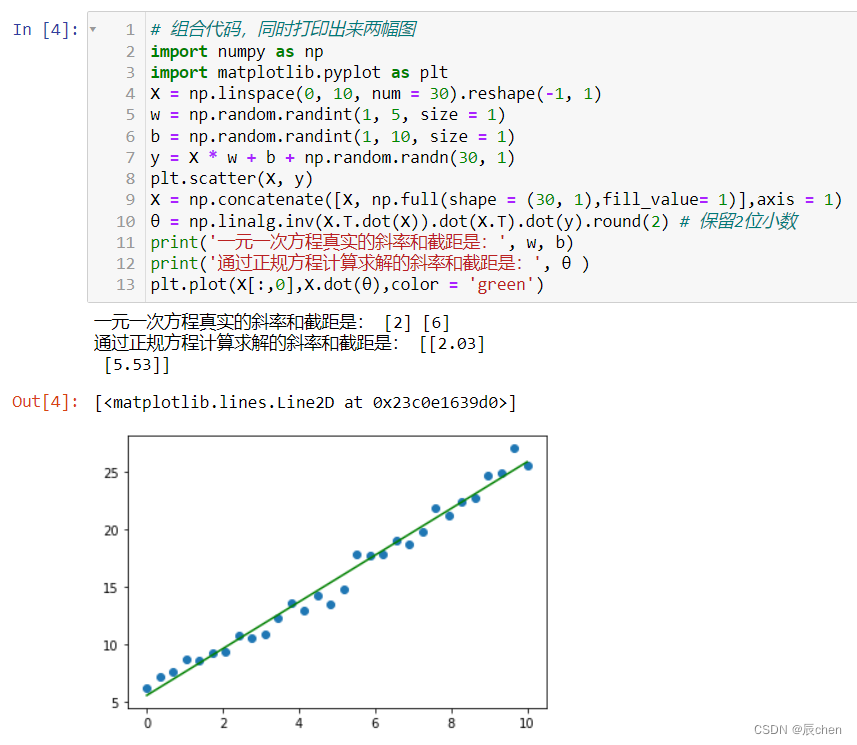
多元线性回归 $y=w1x1+w2x2+b$

Q：为什么仅仅距离二元线性回归？
A：可以绘出3D图，再高维不可绘图，不方便演示

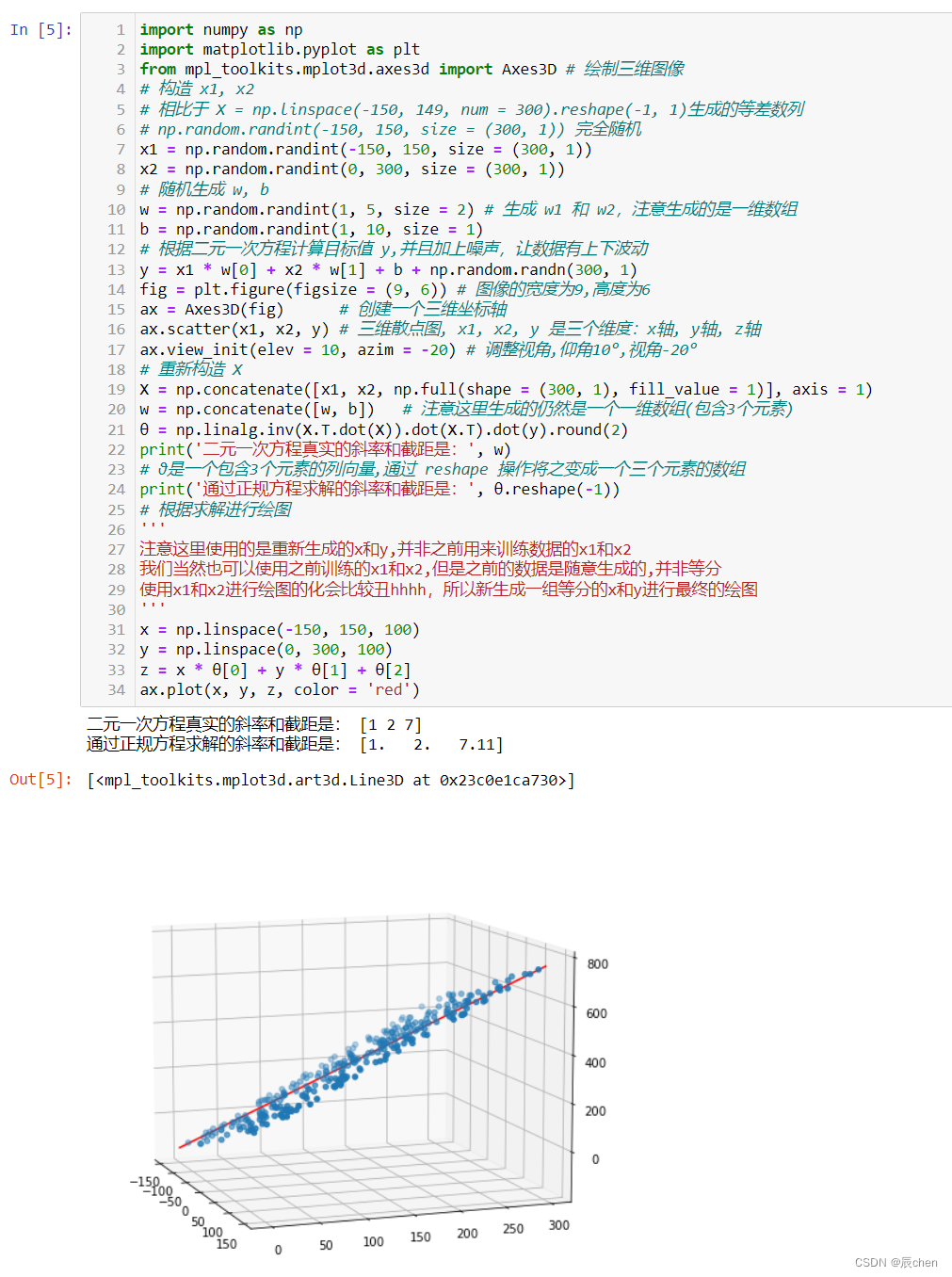
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像
# 构造 x1, x2
# 相比于 X = np.linspace(-150, 149, num = 300).reshape(-1, 1)生成的等差数列
# np.random.randint(-150, 150, size = (300, 1)) 完全随机
x1 = np.random.randint(-150, 150, size = (300, 1))
x2 = np.random.randint(0, 300, size = (300, 1))
# 随机生成 w, b
w = np.random.randint(1, 5, size = 2) # 生成 w1 和 w2，注意生成的是一维数组
b = np.random.randint(1, 10, size = 1)
# 根据二元一次方程计算目标值 y,并且加上噪声，让数据有上下波动
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)
fig = plt.figure(figsize = (9, 6)) # 图像的宽度为9,高度为6
ax = Axes3D(fig)      # 创建一个三维坐标轴
ax.scatter(x1, x2, y) # 三维散点图, x1, x2, y 是三个维度：x轴, y轴, z轴
ax.view_init(elev = 10, azim = -20) # 调整视角,仰角10°,视角-20°
# 重新构造 X 
X = np.concatenate([x1, x2, np.full(shape = (300, 1), fill_value = 1)], axis = 1)
w = np.concatenate([w, b])   # 注意这里生成的仍然是一个一维数组(包含3个元素)
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)
print('二元一次方程真实的斜率和截距是：', w)
# θ是一个包含3个元素的列向量,通过 reshape 操作将之变成一个三个元素的数组
print('通过正规方程求解的斜率和截距是：', θ.reshape(-1))
# 根据求解进行绘图
'''
注意这里使用的是重新生成的x和y,并非之前用来训练数据的x1和x2
我们当然也可以使用之前训练的x1和x2,但是之前的数据是随意生成的,并非等分
使用x1和x2进行绘图的化会比较丑hhhh，所以新生成一组等分的x和y进行最终的绘图
'''
x = np.linspace(-150, 150, 100)
y = np.linspace(0, 300, 100)
z = x * θ[0] + y * θ[1] + θ[2]
ax.plot(x, y, z, color = 'red')

总结

关于二维切片：

上图中的代码：
例一：

import numpy as np# 创建一个二维数组
arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])# 二维切片，提取第一行和第二行，第一列和第二列
slice_2d = arr[:2, :2]print("原始数组：")
print(arr)
print("\n二维切片后的子数组：")
print(slice_2d)

输出：

原始数组：
[[1 2 3][4 5 6][7 8 9]]二维切片后的子数组：
[[1 2][4 5]]

例二：

import numpy as np# 创建一个二维数组
arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])# 切片第一行和第一列
slice_first_row_col = arr[:1, :1]print("原始数组：")
print(arr)
print("\n切片后的子数组：")
print(slice_first_row_col)

输出：

原始数组：
[[1 2 3][4 5 6][7 8 9]]切片后的子数组：
[[1]]

例三：

import numpy as np# 创建一个二维数组
arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])# 切片第二行和第二列
slice_second_row_col = arr[1:2, 1:2]print("原始数组：")
print(arr)
print("\n切片后的子数组：")
print(slice_second_row_col)

输出：

原始数组：
[[1 2 3][4 5 6][7 8 9]]切片后的子数组：
[[5]]

例四：

import numpy as np# 创建一个二维数组
arr = np.array([[1, 2, 3],[4, 5, 6],[7, 8, 9]])# 切片最后一行和最后一列
slice_last_row_col = arr[-1:, -1:]print("原始数组：")
print(arr)
print("\n切片后的子数组：")
print(slice_last_row_col)

输出：

原始数组：
[[1 2 3][4 5 6][7 8 9]]切片后的子数组：
[[9]]

完整截图：