13.二维区域和检索-矩阵不可变

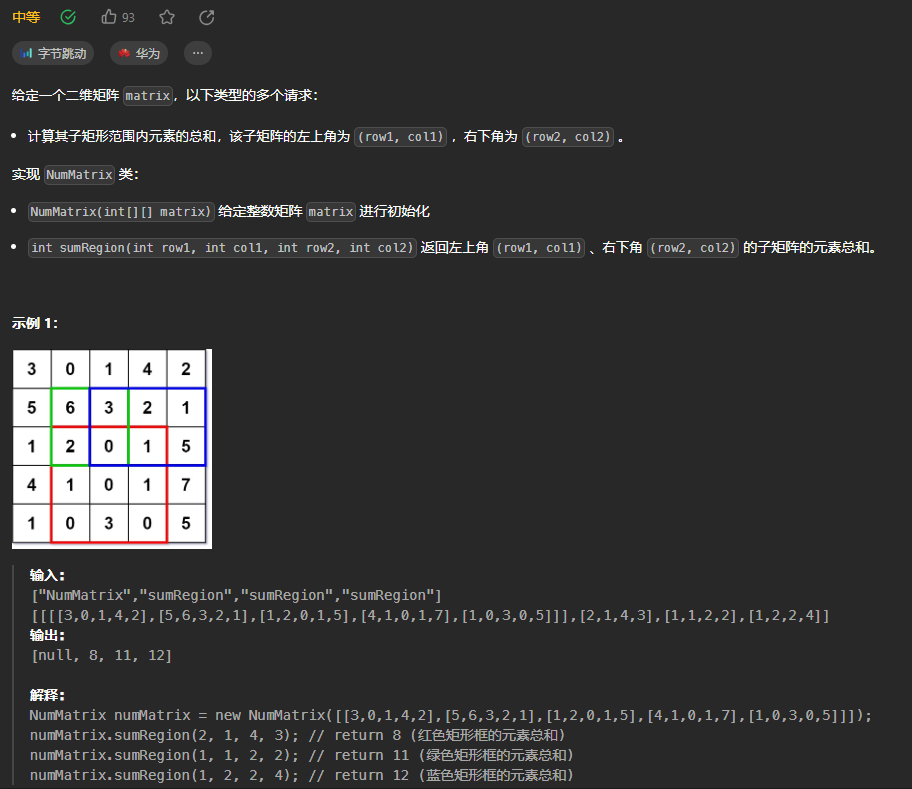
方法：一维前缀和

初始化时对矩阵的每一行计算前缀和，检索时对二维区域中的每一行计算子数组和，然后对每一行的子数组和计算总和。

具体实现方面，创建 m 行 n+1 列的二维数组 sums，其中 m和 n 分别是矩阵 matrix 的行数和列数，sums[i]为 matrix[i] 的前缀和数组。将 sums 的列数设为 n+1 的目的是为了方便计算每一行的子数组和，不需要对 col1=0的情况特殊处理。

class NumMatrix {int[][] sums;public NumMatrix(int[][] matrix) {int m = matrix.length;if(m > 0){int n = matrix[0].length;sums = new int[m][n+1];for(int i = 0;i<m;i++){for(int j = 0;j<n;j++){//对二维区域中每一行计算子数组和，对每一行的子数组计算总和sums[i][j+1] = sums[i][j] + matrix[i][j];}}}}public int sumRegion(int row1, int col1, int row2, int col2) {int sum = 0;for(int i = row1;i<=row2;i++){sum += sums[i][col2+1] - sums[i][col1];}return sum;}
}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* int param_1 = obj.sumRegion(row1,col1,row2,col2);*/