所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

一、题目

二、解法

  思路分析：本题要求为：

• 1.尽可能多的划分片段
• 2.字母只能出现在一个片段中
• 3.片段连接起来仍然是s（只做切割，不改变字母位置）

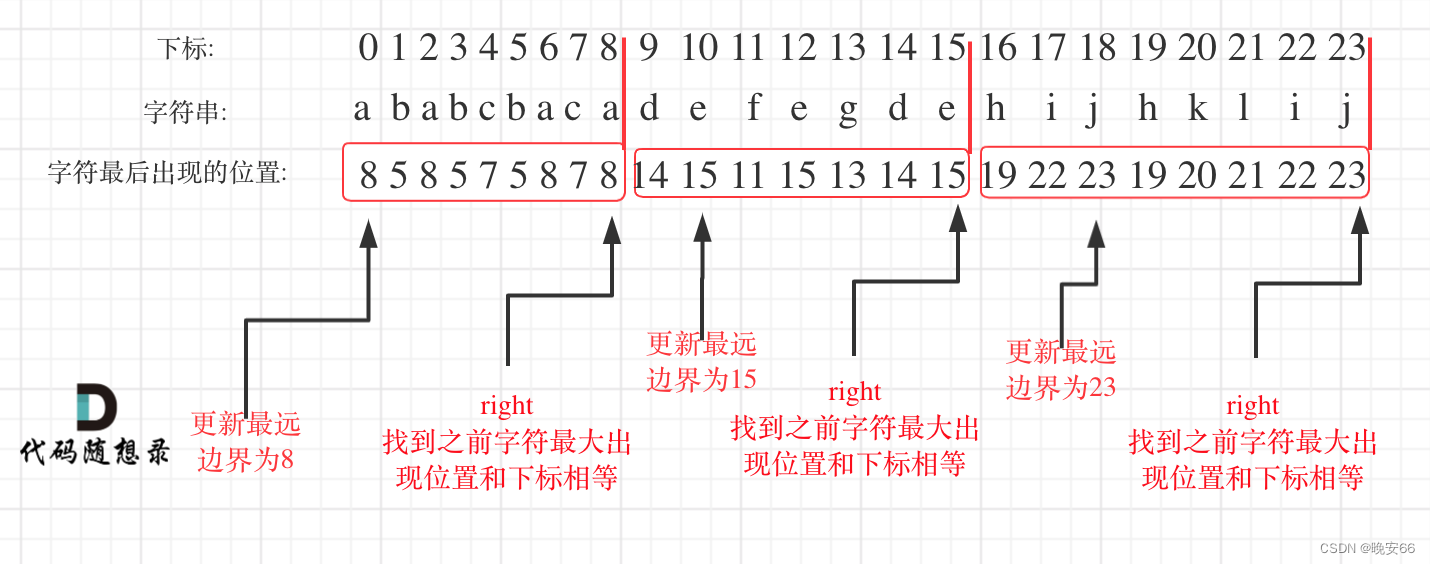
  程序当中我们需要统计字母最后出现的位置，然后找到字符出现的最远边界，当i=最远边界时（从上图可以看出最远边界就是分割点），则找到了分割点。
  程序如下：

class Solution {
public:vector<int> partitionLabels(string s) {// 1.尽可能多的划分片段 2.字母只能出现在一个片段中 3.片段连接起来仍然是s（只做切割，不改变字母位置）vector<int> result;int left = 0;			// 片段的左边界int right = 0;			// 片段的右边界int hash[27] = { 0 };	// 构建字母哈希表for (int i = 0; i < s.size(); i++) {hash[s[i] - 'a'] = i;	// 统计字母最后出现的位置}		for (int i = 0; i < s.size(); i++) {right = max(right, hash[s[i] - 'a']); // 找到字符出现的最远边界if (i == right) {	// 如果i=最远边界，则找到分割点result.push_back(right - left + 1);left = i + 1;}}return result;}
};

复杂度分析：

• 时间复杂度： $O(n)$。
• 空间复杂度：$O(1)$。

三、完整代码

# include <iostream>
# include <vector>
# include <algorithm>
# include <string>
using namespace std;class Solution {
public:vector<int> partitionLabels(string s) {// 1.尽可能多的划分片段 2.字母只能出现在一个片段中 3.片段连接起来仍然是s（只做切割，不改变字母位置）vector<int> result;int left = 0;			// 片段的左边界int right = 0;			// 片段的右边界int hash[27] = { 0 };	// 构建字母哈希表for (int i = 0; i < s.size(); i++) {hash[s[i] - 'a'] = i;	// 统计字母最后出现的位置}		for (int i = 0; i < s.size(); i++) {right = max(right, hash[s[i] - 'a']); // 找到字符出现的最远边界if (i == right) {	// 如果i=最远边界，则找到分割点result.push_back(right - left + 1);left = i + 1;}}return result;}
};int main() {string s = "ababcbacadefegdehijhklij";Solution s1;vector<int> result = s1.partitionLabels(s);for (vector<int>::iterator it = result.begin(); it < result.end(); it++) {cout << *it << ' ';}cout << endl;system("pause");return 0;
}

end