模型融合之模型堆叠-编程知识

模型融合之模型堆叠

一、理论

模型堆叠（Model Stacking）是一种集成学习的方法，其本质是将多个基学习器（Individual Learner）的预测结果作为新的特征，再训练一个元学习器（Meta Learner）来进行最终的预测。每个基学习器可以使用不同的算法或参数来训练，因此理论上你可以将任何可以输出概率值的模型作为基学习器进行模型堆叠。

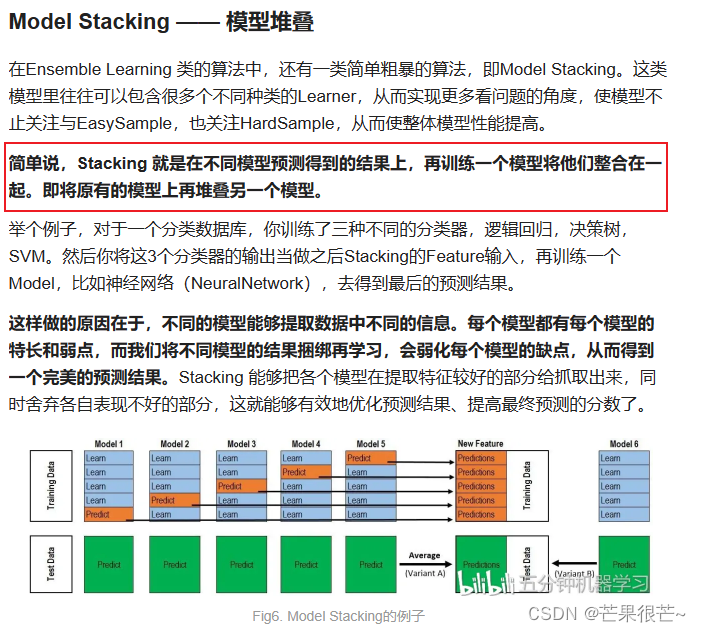
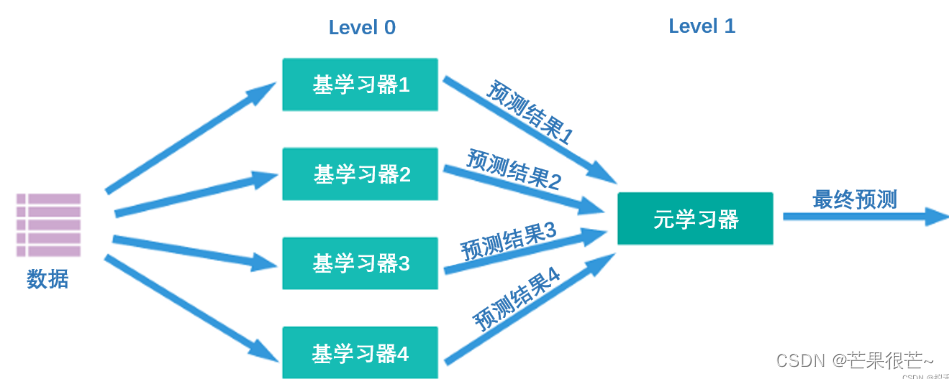
StackingClassifier应用于分类问题，StackingRegressor应用于回归问题。

level 0上训练的多个强学习器被称为基学习器(base-model)，也叫做个体学习器。在level 1上训练的学习器叫元学习器（meta-model）。根据行业惯例，level 0上的学习器是复杂度高、学习能力强的学习器，例如集成算法、支持向量机，而level 1上的学习器是可解释性强、较为简单的学习器，如决策树、线性回归、逻辑回归等。有这样的要求是因为level 0上的算法们的职责是找出原始数据与标签的关系、即建立原始数据与标签之间的假设，因此需要强大的学习能力。但level 1上的算法的职责是融合个体学习器做出的假设、并最终输出融合模型的结果，相当于在寻找“最佳融合规则”，而非直接建立原始数据与标签之间的假设。

二、实例

# 常用工具库
import re
import numpy as np
import pandas as pd
import matplotlib as mlp
import matplotlib.pyplot as plt
import time# 算法辅助 & 数据
import sklearn
from sklearn.model_selection import KFold, cross_validate
from sklearn.datasets import load_digits  # 分类 - 手写数字数据集
from sklearn.datasets import load_iris
#from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split# 算法（单一学习器）
from sklearn.neighbors import KNeighborsClassifier as KNNC
from sklearn.neighbors import KNeighborsRegressor as KNNR
from sklearn.tree import DecisionTreeRegressor as DTR
from sklearn.tree import DecisionTreeClassifier as DTC
from sklearn.linear_model import LinearRegression as LR
from sklearn.linear_model import LogisticRegression as LogiR
from sklearn.ensemble import RandomForestRegressor as RFR
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.ensemble import GradientBoostingClassifier as GBC
from sklearn.naive_bayes import GaussianNB
import xgboost as xgb# 融合模型
from sklearn.ensemble import StackingClassifierdata = load_digits()
X = data.data  #(1797, 64)，代表了1797个样本，每个样本有64个特征，这对应了8x8像素的图片
y = data.target #一维数组，其维度为 (1797,)，包含了对应图片的真实数字标签（0-9）# 划分数据集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, y, test_size=0.2, random_state=1412)def fusion_estimators(clf):"""对融合模型做交叉验证，对融合模型的表现进行评估"""cv = KFold(n_splits=5, shuffle=True, random_state=1412)results = cross_validate(clf, Xtrain, Ytrain , cv=cv , scoring="accuracy", n_jobs=-1, return_train_score=True, verbose=False)test = clf.fit(Xtrain, Ytrain).score(Xtest, Ytest)print("train_score:{}".format(results["train_score"].mean()), "\n cv_mean:{}".format(results["test_score"].mean()), "\n test_score:{}".format(test))def individual_estimators(estimators):"""对模型融合中每个评估器做交叉验证，对单一评估器的表现进行评估"""for estimator in estimators:cv = KFold(n_splits=5, shuffle=True, random_state=1412) #创建了一个5折交叉验证的KFold对象cvresults = cross_validate(estimator[1], Xtrain, Ytrain, cv=cv , scoring="accuracy", n_jobs=-1, return_train_score=True, verbose=False)test = estimator[1].fit(Xtrain, Ytrain).score(Xtest, Ytest)print(estimator[0], "\n train_score:{}".format(results["train_score"].mean()) #训练集得分的平均值, "\n cv_mean:{}".format(results["test_score"].mean())      #交叉验证得分的平均值, "\n test_score:{}".format(test), "\n")                    #测试集得分# estimator包含2个元素的元组('Logistic Regression', LogisticRegression(C=0.1, max_iter=3000, n_jobs=8, random_state=1412))# 逻辑回归没有增加多样性的选项
clf1 = LogiR(max_iter=3000, C=0.1, random_state=1412, n_jobs=8)
# 增加特征多样性与样本多样性
clf2 = RFC(n_estimators=100, max_features="sqrt", max_samples=0.9, random_state=1412, n_jobs=8)
# 特征多样性，稍微上调特征数量
clf3 = GBC(n_estimators=100, max_features=16, random_state=1412)# 增加算法多样性，新增决策树与KNN
clf4 = DTC(max_depth=8, random_state=1412)
clf5 = KNNC(n_neighbors=10, n_jobs=8)
clf6 = GaussianNB()# 新增随机多样性，相同的算法更换随机数种子
clf7 = RFC(n_estimators=100, max_features="sqrt", max_samples=0.9, random_state=4869, n_jobs=8)
clf8 = GBC(n_estimators=100, max_features=16, random_state=4869)estimators = [("Logistic Regression", clf1), ("RandomForest", clf2), ("GBDT", clf3), ("Decision Tree", clf4), ("KNN", clf5)# , ("Bayes",clf6), ("RandomForest2", clf7), ("GBDT2", clf8)]#选择单个评估器中分数最高的随机森林作为元学习器
#也可以尝试其他更简单的学习器
final_estimator = RFC(n_estimators=100, min_impurity_decrease=0.0025, random_state= 420, n_jobs=8)
clf = StackingClassifier(estimators=estimators #level0的7个体学习器,final_estimator=final_estimator #level 1的元学习器,n_jobs=8)
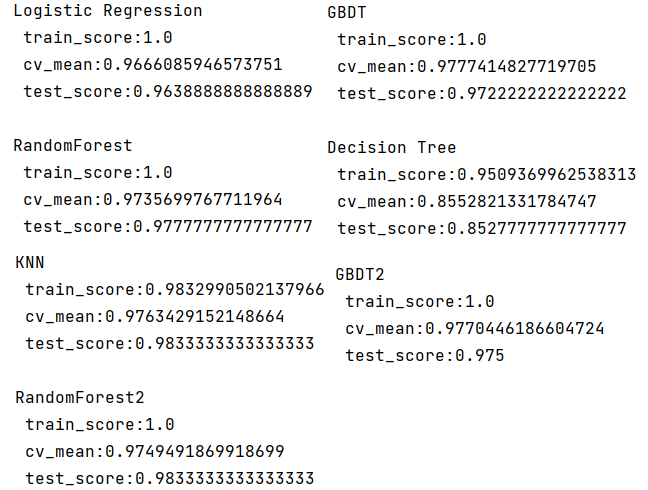
fusion_estimators(clf)
individual_estimators(estimators)

结果：