原文链接：
https://www.sciencedirect.com/science/article/pii/S0306457323000894?via%3Dihub
Information Processing & Management 2023
介绍
问题
可以通过枚举span的方法来解决嵌套实体，然而目前的模型忽略了span之间的语义依赖关系（23年看见两三篇都是对span之间的关系进行建模的）。
IDEA
作者提出了一种planarized 句子表征来表示嵌套实体，并使用一个双向二维的递归操作来学习span之间的语义依赖关系。
方法
整个模型的结构如下图所示，大体上可以分为三个部分：encoder、Bi-TDNN和最后的分类。
Encoder
表示一句长为N的句子，ti表示第i个token。
对于每个token，使用bert embedding、distance embedding（学习句子中token的位置信息）、region embedding（表示在矩阵中的上下三角区域的分布特征）、attention embedding （对与输出相关的输入特征进行加权）这四种不同的embedding来表示不同特征，然后将其进行concate，具体表示如下：
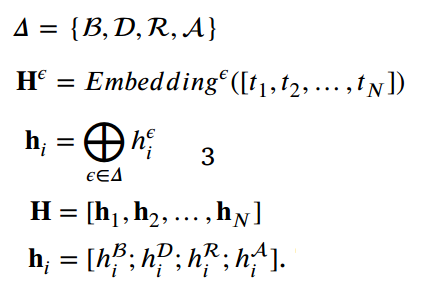
Bi-TDNN
为了得到句子的二维表示，作者设计了两种self-cross。
first self-cross encoding
将序列H作为输入，其中
表示span
平均池化后的结果，即
表示在句子T中跨度为（i，j）的span 表征：
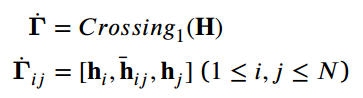
为了对其进行语义特征归一化，使用条件归一化层CLN进行处理：
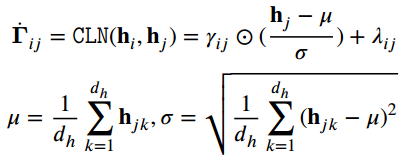
送入一个MLP进行降维，并输入双向二维递归层（没有很get到这一层的具体操作）来学习跨度之间的语义依赖关系。
second self-cross encoding
在bert的输出H上使用两个独立的FFNN，得到两个token序列表征，作者认为这两个token是同一token ti的不同表征（与biaffine一样），可以被视为句子的开始和结束边界表征T，即第二种self-cross encoding表示为：
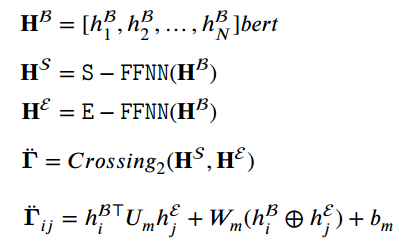
将这两种self-cross encoding的结果进行残差连接，得到句子T的平面语义表征：
Bidirectional two-dimensional convolution
中的元素表示span的表征，语义上是独立的，即L的分布可以通过以下公式进行计算：
根据一阶马尔可夫假设，上式可进行化简等价，即每个标签Lij只取决于其相邻span表征
：
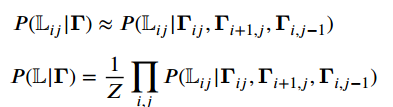
作者使用一个包含GRU的双向二维递归神经网络Bi-TDNN来学习语义依赖：
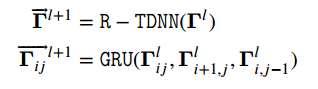
R-TDNN从左上角到右下角的整个语义平面上进行迭代执行，学习了语义依赖关系，但由于span之间的依赖是双向的，因此还需要从右下角到左上角建立一个基于网格的时延神经网络，以便将语义依赖向另一个方向倾斜：
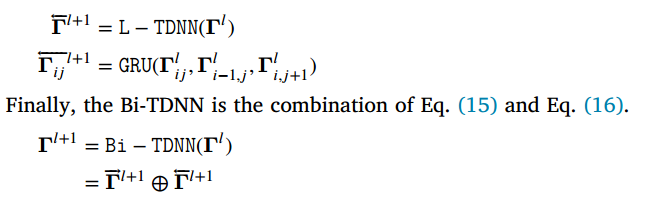
Training objective
将
结合得到的F进行分类：
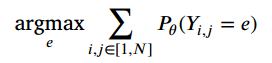
模型的loss为：
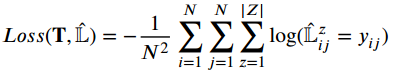
实验
对比实验
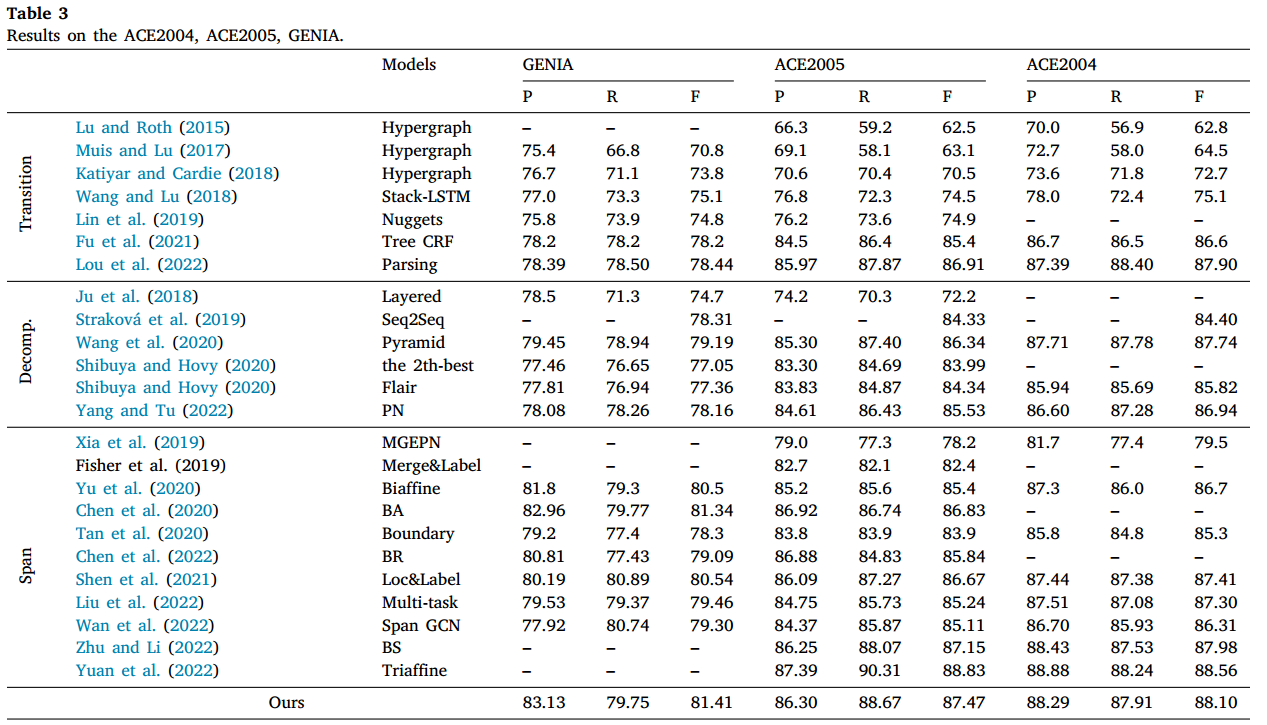
在genia、ace2005和ace2004这三个数据集上进行实验，结果如下图所示：
在NNE和KBP17数据集上进行实验，结果如下所示：
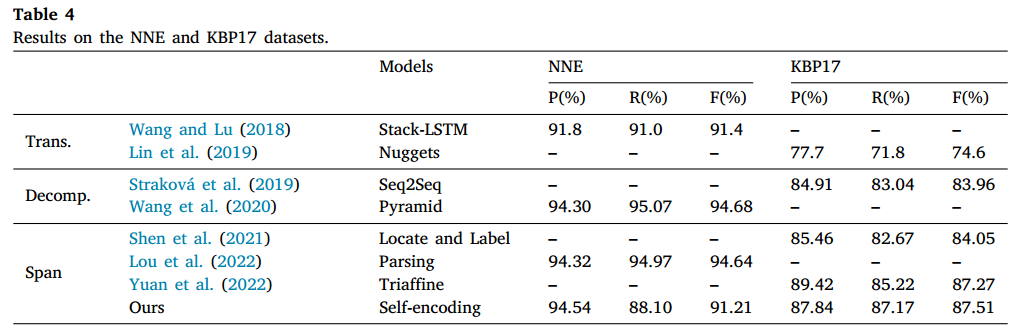
作者认为与其他方法相比，作者的模型达到了competitive performance。平面化句子表示具有解决嵌套结构和使用跨度语义特征的优势，并且这种表示方法能够实现二维循环，有效的学习span之间的语义依赖关系。
在两个flat数据集上进行实验，结果如下图所示：
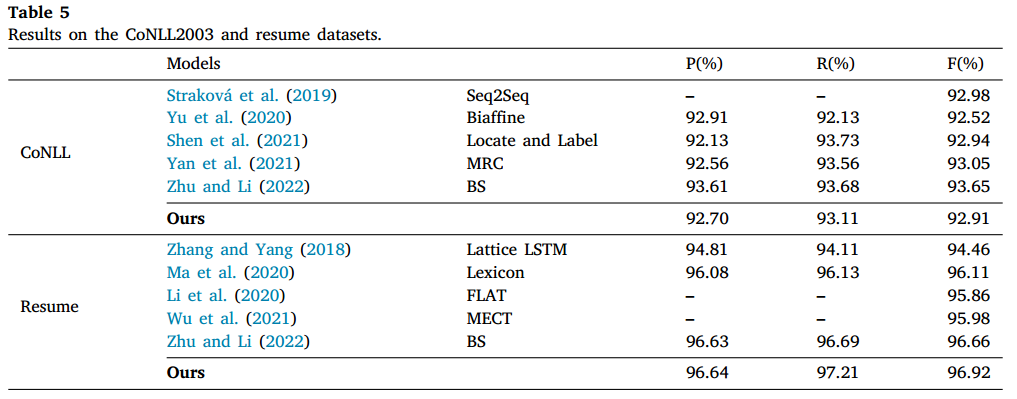
消融实验
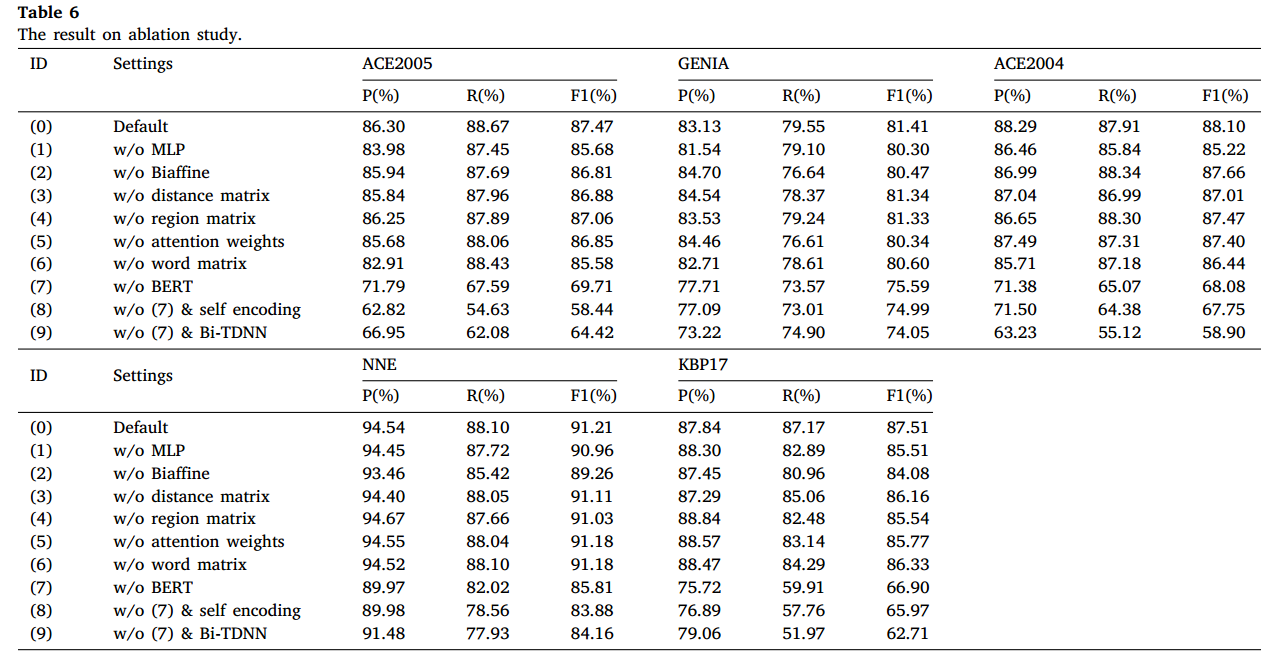
对多个模块进行消融实验，结果如下所示：
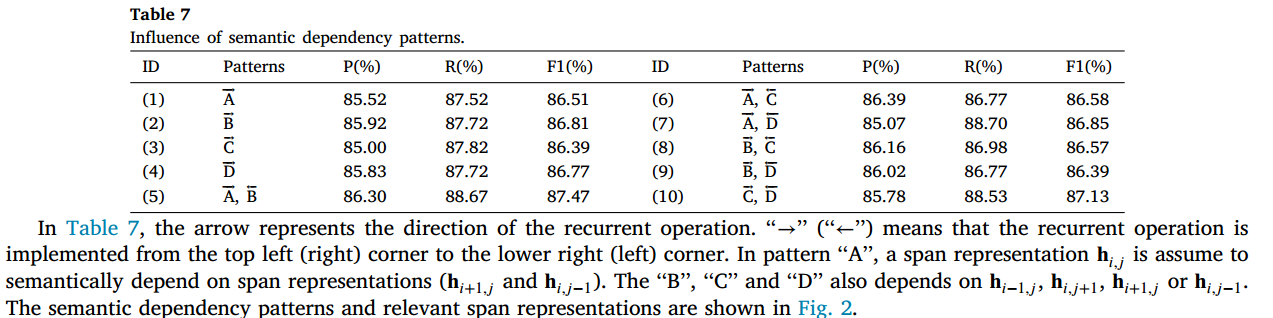
在每个方向上，二维递归操作假设了两个方向上的语义依赖，从而产生了四种语义依赖模式。该实验旨在证明语义依赖模式在 Bi-TDNN 模块中的影响，实验结果如下所示：
其他实验
层数对结果的影响：
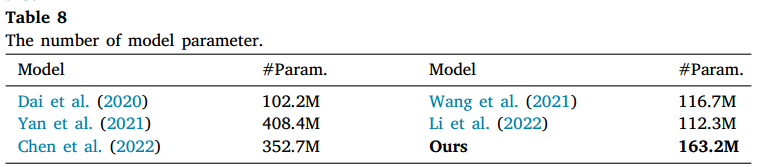
参数量：
总结
对span之间的语义关系进行建模也算不上太新的idea，而且二维递归网络那里没有很看懂，而且论文的结构我感觉怪怪的，用的符号也怪怪的（是我看太少了？）。实验结果也不是很好，而作者也并没有对实验结果进行具体分析，只是提了一句competitive，感觉不太能说服人。不过做了很多的实验，消融实验那个地方也是，感觉怪怪的。
