一道练习单调栈 + 单调队列的好题
题目链接:problem
对于求合法子数组数量的题目,可以先考虑传统的枚举右端点,二分左端点的套路。此题用这种方法恰好可行,因为对于一个序列,左端增加一个数不会让操作数更少。因此对于固定右端点,合法的左端点一定是一段区间。
所以现在问题转化为:用双指针枚举子区间左右端点,滑动窗口累计操作数。而计算操作数就需要使用数据结构来实时维护
序列变化只由两种操作触发:
- 枚举右端点时,右端点右移时,子数组右端多了一个数
- 左端点右移时,子数组左端少了一个数
对于\(1\) : 当原序列右端多了一个数 \(x\) 时,其他元素的贡献是不变的,只有刚加入的数会产生新的贡献:即为原序列内最大值\(mx - x\)。而滑动窗口的最大值可以用单调队列来维护。
对于\(2\) : 当原序列左端少了一个数 \(x\) 时,该数的移除会使得后面所有数的贡献均发生变化。这里是用单调栈建树的方式完成的,很冷门与抽象。还是直接看灵神题解吧qwq...
链接:sol
![[megatron代码阅读] 1. 初始化和组网](https://img2023.cnblogs.com/blog/1439743/202501/1439743-20250109211043913-1425120685.png)
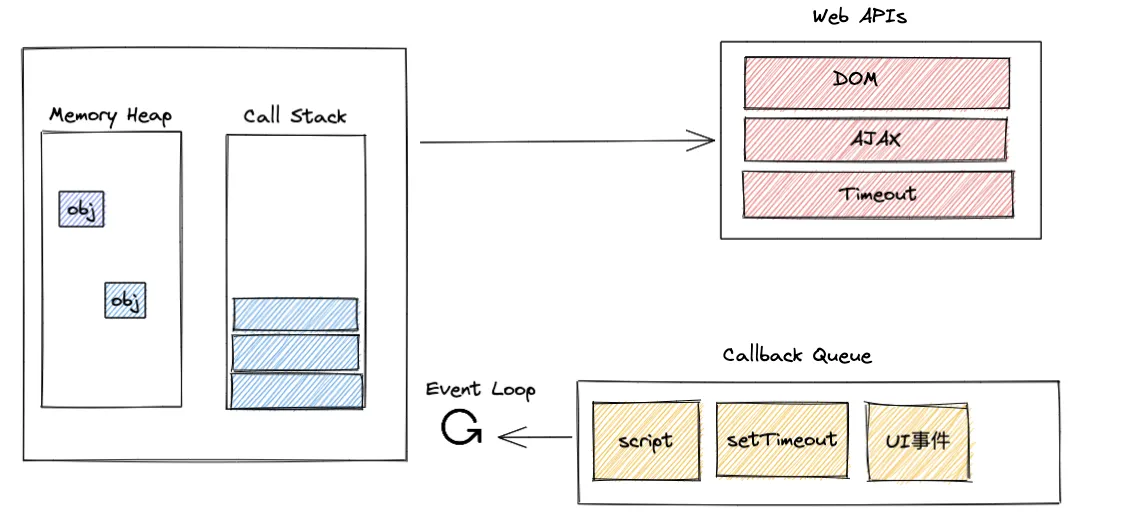





![题解:AT_abc353_f [ABC353F] Tile Distance](https://cdn.luogu.com.cn/upload/image_hosting/58f4e31e.png)