直线上有9个格子,4个石子,
| 数量 | 结构编号 | |||||||||
| 6 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 5 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 4 | 4 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 3 | 5 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
有6个不同的结构
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
如结构5可能的置换有3个。这6个结构置换的数量顺序为0>2=1>3=4>5.
(A,B)---1*n*2---(1,0)(0,1)
做一个网络分类A和B,让A就是这6个结构,B全是0.用训练集做测试集
| A | B | 1-0 | 0-1 | ||
| 1 | 0 | 0.444 | 1 | 0.722 | |
| 0*1 | 1 | 0 | 0.5 |
这个网络可能的合理分类方法只有两种,一种是认为1属于A,0属于B,则A的分类准确率是0.444,B的分类准确率是1,因为两个测试集图片数量相同,所以总的分类准确率是0.722.第二种方法是认为0和1都属于A,则A的准确率是1,B为0,平均是0.5.
现在让这个网络的隐藏层节点数为
| 20 | 16 | 15 | 12 | 10 | 8 | 6 | 4 | 2 | |
| 210 | 190 | 170 | 150 | 130 | 110 | 90 | 70 | 50 | 30 |
| 410 | 390 | 370 | 350 | 330 | 310 | 290 | 270 | 250 | 230 |
| 610 | 590 | 570 | 550 | 530 | 510 | 490 | 470 | 450 | 430 |
| 810 | 790 | 770 | 750 | 730 | 710 | 690 | 670 | 650 | 630 |
2到810的共49个值,收敛误差为7e-4,每个n的每个结构收敛199次,取平均值。比较迭代次数和分类准确率的变化。
得到的6个结构的顺序为
| 810 | 5 | 4 | 1 | 0 | 3 | 2 | 310 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 790 | 5 | 4 | 2 | 3 | 0 | 1 | 290 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 770 | 4 | 5 | 3 | 1 | 0 | 2 | 270 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 750 | 5 | 4 | 0 | 3 | 1 | 2 | 250 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 730 | 5 | 4 | 0 | 3 | 2 | 1 | 230 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 710 | 5 | 4 | 3 | 0 | 2 | 1 | 210 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 690 | 5 | 4 | 3 | 0 | 2 | 1 | 190 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 670 | 5 | 3 | 4 | 0 | 2 | 1 | 170 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 650 | 4 | 5 | 0 | 3 | 2 | 1 | 150 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 630 | 4 | 3 | 0 | 5 | 2 | 1 | 130 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 610 | 0 | 5 | 3 | 4 | 2 | 1 | 110 | 0 | 1 | 2 | 3 | 4 | 5 | |
| 590 | 3 | 0 | 1 | 4 | 2 | 5 | 90 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 570 | 3 | 0 | 1 | 2 | 4 | 5 | 70 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 550 | 3 | 0 | 1 | 2 | 4 | 5 | 50 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 530 | 1 | 3 | 0 | 2 | 4 | 5 | 30 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 510 | 1 | 3 | 0 | 2 | 4 | 5 | 20 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 490 | 1 | 3 | 0 | 2 | 4 | 5 | 16 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 470 | 1 | 3 | 0 | 2 | 4 | 5 | 15 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 450 | 3 | 0 | 1 | 2 | 4 | 5 | 12 | 0 | 2 | 1 | 3 | 5 | 4 | |
| 430 | 0 | 3 | 1 | 2 | 4 | 5 | 10 | 0 | 2 | 3 | 1 | 4 | 5 | |
| 410 | 0 | 1 | 3 | 2 | 4 | 5 | 8 | 2 | 0 | 1 | 3 | 5 | 4 | |
| 390 | 0 | 1 | 3 | 2 | 4 | 5 | 6 | 0 | 2 | 3 | 4 | 1 | 5 | |
| 370 | 0 | 1 | 3 | 2 | 4 | 5 | 4 | 5 | 0 | 1 | 2 | 3 | 4 | |
| 350 | 0 | 1 | 2 | 3 | 4 | 5 | 2 | 0 | 2 | 1 | 3 | 4 | 5 | |
| 330 | 0 | 1 | 2 | 3 | 4 | 5 |
只有16-90的第Ⅱ区顺序是稳定的,并且和计算顺序一致。n<16或n>90的顺序都变得混乱。
比较迭代次数的数据
| 比值 | 乘积 | ||||||||
| 810 | 747.4422 | 753 | 764.6482 | 767.8543 | 773.0905 | 781.4121 | 1.05 | 632943.8 | |
| 790 | 755.0704 | 759.9146 | 775.8945 | 784.4372 | 785.2211 | 786.1558 | 1.04 | 621063.1 | |
| 770 | 765.1106 | 767.0503 | 787.4824 | 789.6935 | 795.5327 | 798.5176 | 1.04 | 614858.5 | |
| 750 | 771.794 | 774.3869 | 793.7236 | 803.794 | 805.3819 | 805.8945 | 1.04 | 604420.9 | |
| 730 | 776.4673 | 784.9698 | 804.8492 | 808.1156 | 815.2513 | 819.0101 | 1.05 | 597877.3 | |
| 710 | 786.6683 | 795.3518 | 805.4523 | 812.3568 | 822.8794 | 826.2663 | 1.05 | 586649.1 | |
| 690 | 801.7035 | 806.7588 | 812.3568 | 821.3116 | 831.0302 | 846.0754 | 1.06 | 583792 | |
| 670 | 818.5377 | 819.9347 | 820.7286 | 834.0653 | 837.9146 | 859.0402 | 1.05 | 575556.9 | |
| 650 | 826.8894 | 833.7538 | 847.995 | 849.7136 | 859.5528 | 908.0151 | 1.1 | 590209.8 | |
| 630 | 832.2764 | 859.1407 | 860.1156 | 862.4271 | 914.2462 | 945.794 | 1.14 | 595850.2 | |
| 610 | 872.6884 | 879.7839 | 892.9497 | 904.2965 | 930.3467 | 960.9899 | 1.1 | 586203.9 | |
| 590 | 926.3266 | 926.6884 | 952.8693 | 958.4372 | 982.7889 | 1156.698 | 1.25 | 682452.1 | |
| 570 | 976.3467 | 979.0603 | 991.8543 | 1012.638 | 1069.603 | 1244.196 | 1.27 | 709191.7 | |
| 550 | 1039.211 | 1047.171 | 1050.266 | 1053.452 | 1175.161 | 1336.819 | 1.29 | 735250.5 | |
| 530 | 1100.377 | 1107.774 | 1129.935 | 1140.015 | 1286.236 | 1466.618 | 1.33 | 777307.6 | |
| 510 | 1174.186 | 1191.261 | 1219.844 | 1245.482 | 1438.377 | 1666.879 | 1.42 | 850108.5 | |
| 490 | 1274.859 | 1292.116 | 1323.503 | 1374.92 | 1640.085 | 1977.854 | 1.55 | 969148.6 | |
| 470 | 1404.749 | 1409.704 | 1437.834 | 1525.704 | 1896.789 | 2436.899 | 1.73 | 1145343 | |
| 450 | 1561.211 | 1567.362 | 1569.191 | 1716.648 | 2226.307 | 3075.854 | 1.97 | 1384134 | |
| 430 | 1718.779 | 1754.688 | 1765.563 | 1948.025 | 2664.005 | 3967.08 | 2.31 | 1705845 | |
| 410 | 1902.487 | 2008.518 | 2009.221 | 2239.734 | 3261.804 | 5170.276 | 2.72 | 2119813 | |
| 390 | 2130.698 | 2314.065 | 2372.749 | 2602.085 | 4089.613 | 6795.342 | 3.19 | 2650183 | |
| 370 | 2442.759 | 2705.543 | 2892.035 | 3059.955 | 4988.085 | 8947.834 | 3.66 | 3310699 | |
| 350 | 2902.437 | 3206.196 | 3617.05 | 3634.286 | 6105.302 | 11611.92 | 4 | 4064174 | |
| 330 | 3580.467 | 3834.568 | 4301.141 | 4670.055 | 7456.749 | 14825.29 | 4.14 | 4892346 | |
| 310 | 4480.106 | 4639.683 | 5159.261 | 6043.482 | 9064.266 | 18442.67 | 4.12 | 5717227 | |
| 290 | 5409.503 | 5606.799 | 6218.095 | 7723.181 | 10894.39 | 22193.55 | 4.1 | 6436130 | |
| 270 | 6202.95 | 6754.095 | 7529.472 | 9602.146 | 12904.78 | 25645.17 | 4.13 | 6924196 | |
| 250 | 6879.261 | 8087.814 | 9140.698 | 11564.15 | 15053.65 | 28624.63 | 4.16 | 7156157 | |
| 230 | 7539.472 | 9633.01 | 11109.66 | 13480.83 | 17323.91 | 30956.28 | 4.11 | 7119944 | |
| 210 | 8259.925 | 11394.75 | 12548.27 | 15324.88 | 19684.45 | 32700.39 | 3.96 | 6867081 | |
| 190 | 9140.116 | 13358.02 | 13594.44 | 16876.72 | 22087.49 | 33990.51 | 3.72 | 6458196 | |
| 170 | 10199.22 | 14788.86 | 15172.74 | 18641.08 | 23904.1 | 34084.14 | 3.34 | 5794303 | |
| 150 | 11521.18 | 16116.43 | 16294.62 | 20568.49 | 24188.75 | 32346.82 | 2.81 | 4852023 | |
| 130 | 13172.66 | 17641.18 | 17681.79 | 22395.26 | 24748.56 | 31508.51 | 2.39 | 4096106 | |
| 110 | 15335.37 | 19483.33 | 19552.62 | 24494.39 | 25861.12 | 31575.62 | 2.06 | 3473319 | |
| 90 | 18231.47 | 21967.69 | 22060.23 | 26975.49 | 27672.07 | 32541.56 | 1.78 | 2928741 | |
| 70 | 22283.1 | 25434.01 | 25893.23 | 30198.58 | 30638.54 | 34406.15 | 1.54 | 2408430 | |
| 50 | 28214.42 | 30471.65 | 31501.27 | 34627.12 | 35155.54 | 37923.02 | 1.34 | 1896151 | |
| 30 | 38335.66 | 39628.41 | 40700.18 | 42628.53 | 43286.57 | 44890.92 | 1.17 | 1346728 | |
| 20 | 47392.38 | 48605.16 | 49894.38 | 50763.62 | 51584.3 | 52764.43 | 1.11 | 1055289 | |
| 16 | 53654.12 | 55215.5 | 55892.45 | 56862.55 | 57756.04 | 58652.06 | 1.09 | 938432.9 | |
| 15 | 56311.78 | 56624.75 | 57703.21 | 58880.99 | 59387.43 | 60366.67 | 1.07 | 905500 | |
| 12 | 64075.93 | 64656.91 | 65501.91 | 66791.22 | 67267.99 | 67753.18 | 1.06 | 813038.2 | |
| 10 | 71077.3 | 71915.43 | 73532.09 | 73680.97 | 74362.53 | 75526.56 | 1.06 | 755265.6 | |
| 8 | 84117.8 | 84531.26 | 85455.77 | 85712.93 | 86315.25 | 86410.77 | 1.03 | 691286.2 | |
| 6 | 103357.2 | 104393.6 | 105619.4 | 105846.8 | 105909.8 | 106796.6 | 1.03 | 640779.8 | |
| 4 | 148083.9 | 148184.7 | 148217.1 | 148629.3 | 150324.7 | 150991 | 1.02 | 603963.9 | |
| 2 | 259206.7 | 259809.3 | 260652.9 | 261047.7 | 261532.5 | 262058.4 | 1.01 | 524116.8 |
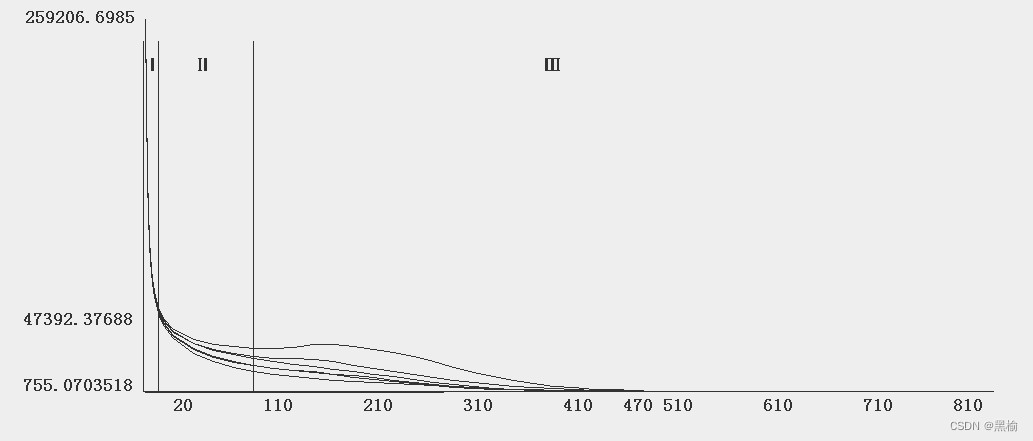
把中间段的曲线放大
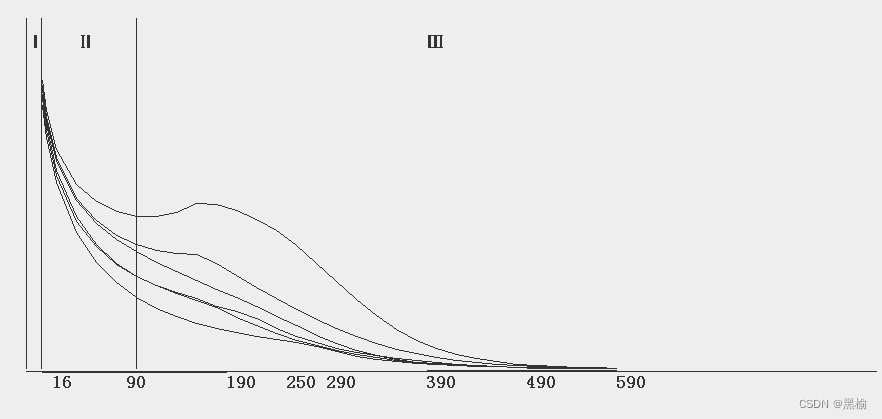
16-90区域几乎就是这条曲线分布最为规则的区域,分布稀疏间距均匀。
特别比较每组隐藏层节点数和迭代次数乘积的曲线
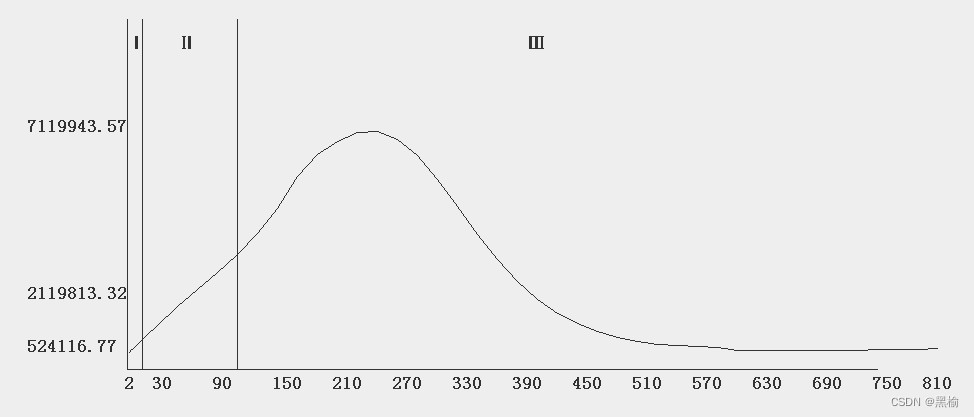
比如当n为2或810时
| 810 | 781.4121 | 632943.8 | |
| 2 | 262058.4 | 524116.8 |
随着n的增加迭代次数d减小,但是n*d从没有小于524116的,当n=690的时候d已经和n相当,但是d的减小量小于n的增加量。所以在收敛误差一定的情况下n*d有极小值。就是2d=524116。所以用这个办法估算当n=100时的最大迭代次数应不小于5241,真实数值为这个数的6.6倍。
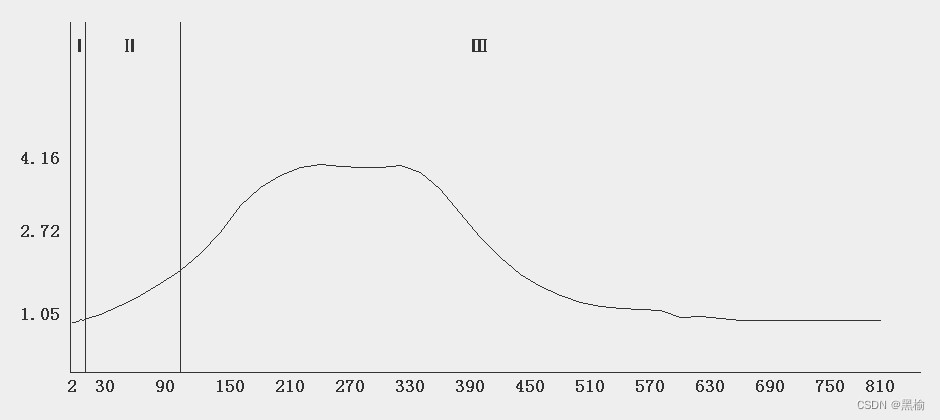
再比较同组迭代次数最大值和最小值的比例,在16-90区域这个值为1.09-1.78.这个值最大值为4.16.这条曲线和n*d的曲线很接近,结构上左右对称。
比较分类准确率
| 810 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 790 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 770 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 750 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 730 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 710 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 690 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 670 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 650 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 630 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 610 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 590 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 570 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 550 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 530 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 510 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 490 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 470 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 450 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 430 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 410 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 390 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 370 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 350 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 330 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 310 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 290 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 270 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 250 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 230 | 0.722222 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 210 | 0.722222 | 0.5 | 0.722222 | 0.5 | 0.5 | 0.5 |
| 190 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 170 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| 150 | 0.5 | 0.5 | 0.5 | 0.5 | 0.722222 | 0.722222 |
| 130 | 0.5 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 110 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 90 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 70 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 50 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 30 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 20 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 16 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 15 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 12 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 10 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 8 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 6 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 4 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
| 2 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 | 0.722222 |
很意外的是Ⅰ区的分类准确率和Ⅱ区是相同的,而Ⅲ区用的第二种分类方法,分类性能从n=130开始变化。
Ⅰ区n<16,尽管迭代次数顺序混乱,但这并不影响分类性能
Ⅱ区16-90,迭代次数顺序和计算顺序一致,分类与计算结果也相同
Ⅲ区n>90,迭代次数顺序开始混乱,网络分类性能开始退化