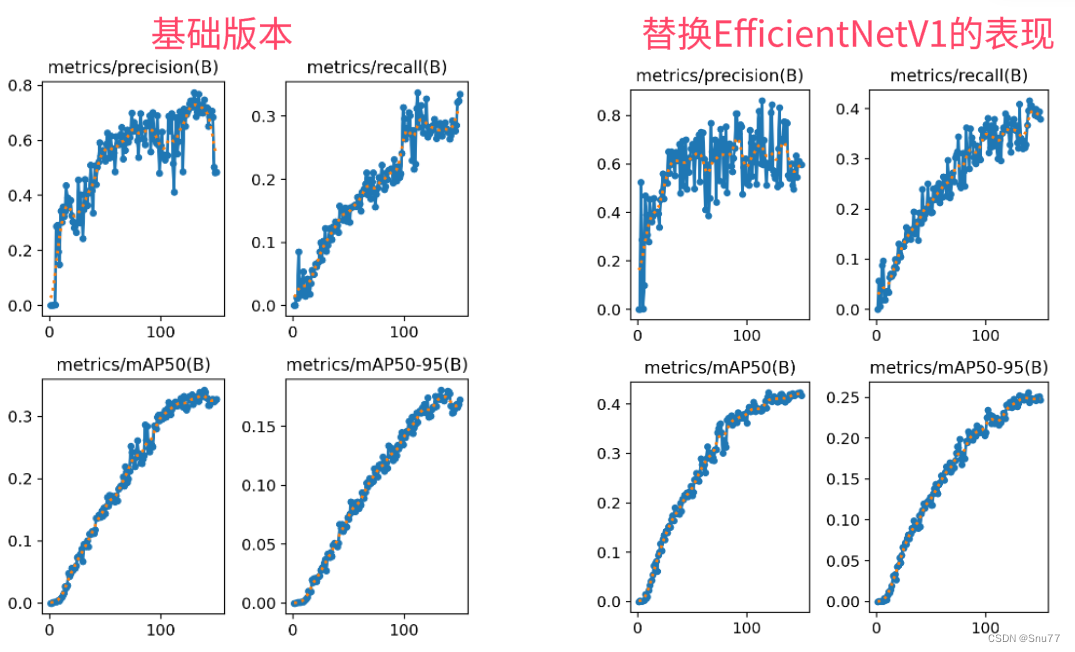
CEC2017中的测试
本文作者将介绍一个2023年发表在中科院1区期刊《Knowledge -Based Systems》上的优化算法——开普勒优化算法(Kepler optimization algorithm,KOA)[1]

算法性能上,与鹈鹕、黏菌、灰狼和鲸鱼等一众优化算法在CEC2014、CEC2017、CEC2020和CEC2022上进行了测试,均显示出其惊艳的性能。因此,感兴趣的各位就和作者一起学习一下该算法的巧妙之处吧,并且,在文章的最后也给出了算法的MATLAB和Python实现。将这样性能较好的新算法应用于一些工程问题也能够在一定程度上提升文章的创新性。
00 目录
1 开普勒优化算法(KOA)原理
2 代码目录
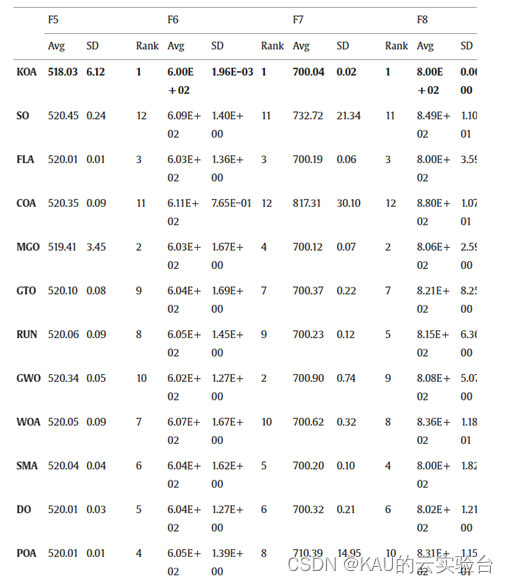
3 算法性能
4 源码获取
01 开普勒优化算法(KOA)原理
图源文献[1]
KOA为基于物理的优化器(意味着公式会比较多…作者这里就列出核心公式来帮助大家理解),是受开普勒行星运动定律启发的新型优化算法。太阳(最优解)和在椭圆轨道上绕它旋转的行星(候选解)构成了搜索空间,在不同的时间,行星将处于轨道中的不同位置,这种策略有效的执行了勘探与开发(如下)。太阳与行星的吸引力、旋转速度等因素也共同决定了行星与太阳的接近程度。为适配该算法,术语“时间”将更适合迭代一词。

图源文献[1]
1.1 初始化
KOA的种群初始化与其他算法相同,每个行星将放置在轨道上的随机位置,算式为xi=lb+rand*(ub-lb)。除此之外,KOA还有两个新的参数需要初始化,即轨道偏心率e和轨道周期T,其计算:
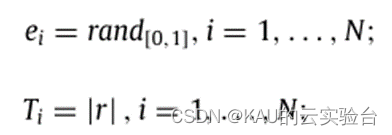
其中,rand为随机值,r为正态分布的随机数。ei与后文中的引力有关,能够赋予KOA一定随机性。而T与椭圆轨道半长轴长度有关,而半长轴长度将随着时间逐渐减小,对应的解也将向可能找到全局最优解的有希望区域移动。
1.2 天体速度
天体的速度受太阳的引力影响,当一颗行星靠近太阳时,它的速度会增加,当它移得更远时,它的速度会降低。如果行星靠近太阳,那么太阳的引力就会相当强,行星就会试图增加自己的速度,以避免被拉向太阳。然而,如果一个物体远离太阳,那么它的速度就会减慢,因为太阳的引力很弱。其关系可由下列方程表示:
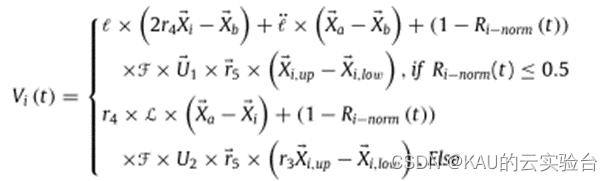
其中具体参数的意义这里不作详解,但可以看到这个公式根据与最优解的距离进行了勘探与开发之间的转换。
1.3 跳出局部最优
在太阳系中,大多数天体都是逆时针绕太阳旋转,它们都绕着自己的轴旋转;然而,也有一些天体是顺时针绕太阳旋转。该算法利用这种行为来逃避局部最优区域,即通过使用标志F(即1.2中的F),改变搜索方向,使代理能够准确地扫描搜索空间。
1.4 更新天体位置
天体在各自的椭圆轨道上围绕太阳旋转。在旋转过程中,物体在一定时间内向太阳靠近,然后远离太阳。KOA通过两个主要阶段模拟这种行为:探索和开发阶段。KOA探索远离太阳的行星以寻找新的解决方案,同时更准确地使用靠近太阳的解决方案,因为它在最佳解决方案附近寻找新的地方。图4显示了太阳周围的勘探和开发区域。

图源文献[1]
行星的位置使用下式更新:

当行星远离太阳时,行星的速度将代表KOA的探索算子。然而,这个速度受到太阳引力的影响,这有助于当前行星略微利用最佳解附近的区域。与此同时,当行星接近太阳时,它的速度急剧增加,使其能够逃脱太阳的引力。在这种情况下,如果迄今为止最好的解(称为太阳)是局部最小值,则速度表示局部最优避免,并且太阳的引力表示利用算子以帮助KOA攻击迄今为止最好的解以找到更好的解。
其中,太阳通过引力控制行星以椭圆的形式绕着其运动,遵循万有引力定律,其定义式:
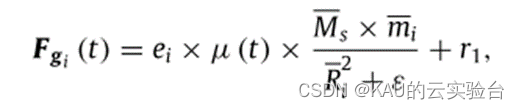
1.5 更新与太阳的距离
为进一步改善行星的探索与开发,算法模仿了太阳与行星之间的距离的典型行为,当行星靠近太阳时,KOA将专注于优化开发算子;当远离太阳时,KOA将优化探索算子。而规则的转换将取决于调节参数h,其随时间逐渐变化。h如下:
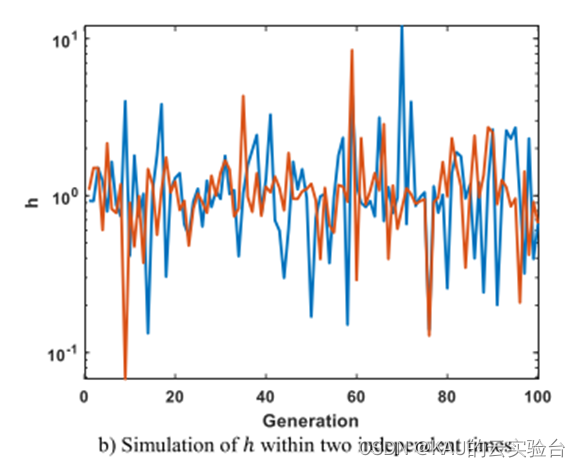
图源文献[1]
当h被设置为一个高值时,重点放在探索算子上,导致行星和太阳之间间隔扩大。相反,当h假设一个低的值,倾向于开发,使得能够在迄今为止获得的最佳解附近进行集中探索。
该原理的数学模型描述如下:
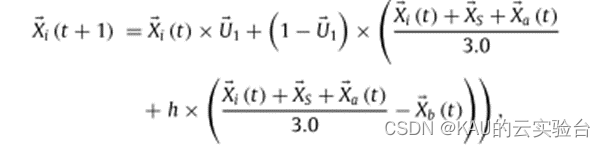
1.6 精英保留
该步骤相当于贪婪策略,若位置更新后适应度更佳则保留。
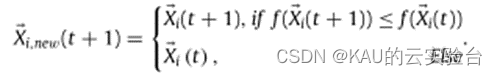
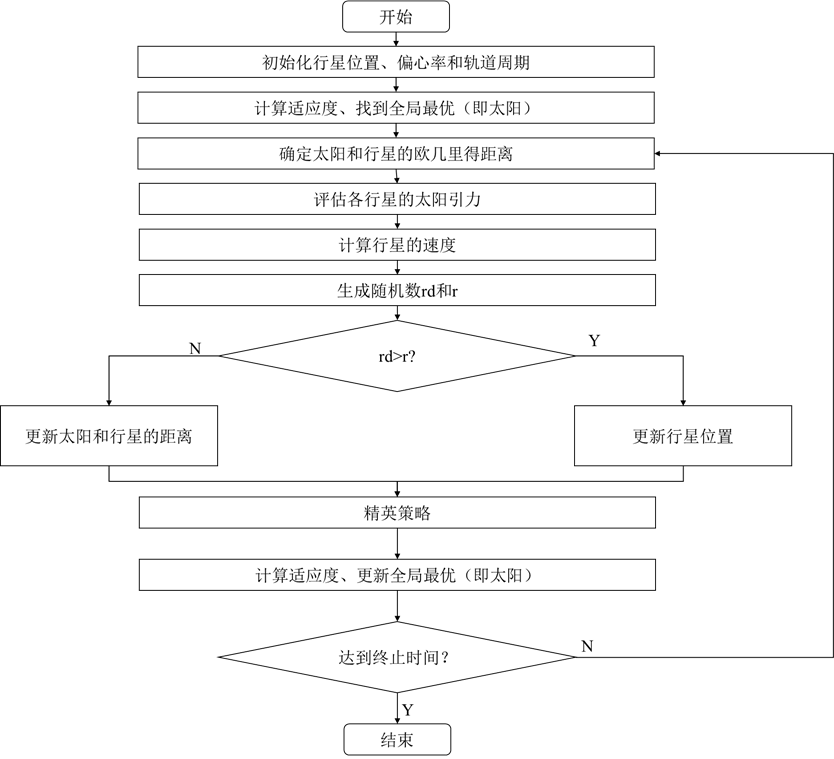
1.7 算法流程
1.8 算法利用
其实在15年和22年都有文献将开普勒混合于优化算法中来提升性能,但这些算法运用的只是开普勒第一定律,形式如下:
其简化程度高,是通过将太阳位置乘均匀分布的伪随机数或通过在太阳位置和行星之间添加距离分量来集中搜索。而在KOA中是一个完整的优化框架,能够更有效的利用和探索空间。其天体位置更新中,既有能够跳出局部最优的策略,也能够进行勘探与开发之间的有效转换,可以将其考虑引入其他算法提升性能。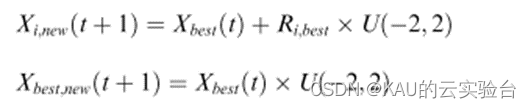
02 代码目录
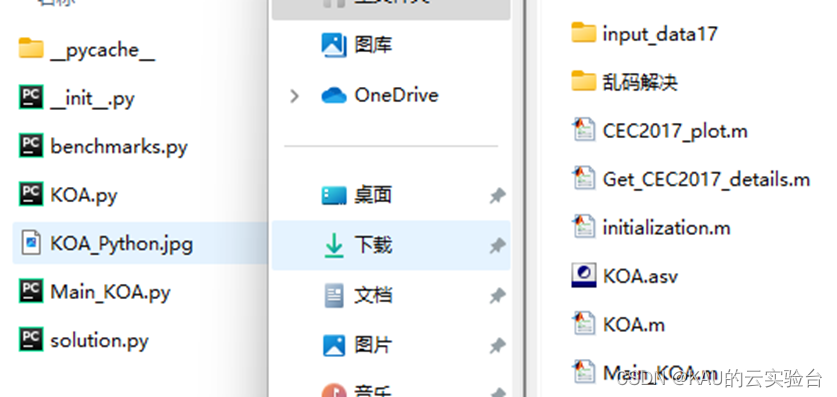
代码包含MATLAB和Python以及KOA算法源文献,考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),可以将MATLAB版本改为2020及以上,或使用乱码解决文件夹中的txt文件即可。
代码都经过作者重新注释,代码更清爽,可读性强。
部分代码:(MATLAB与Python)
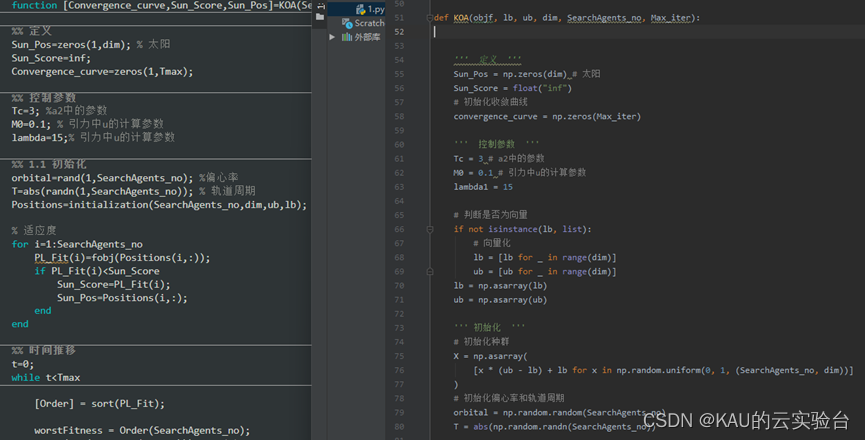
03 算法性能
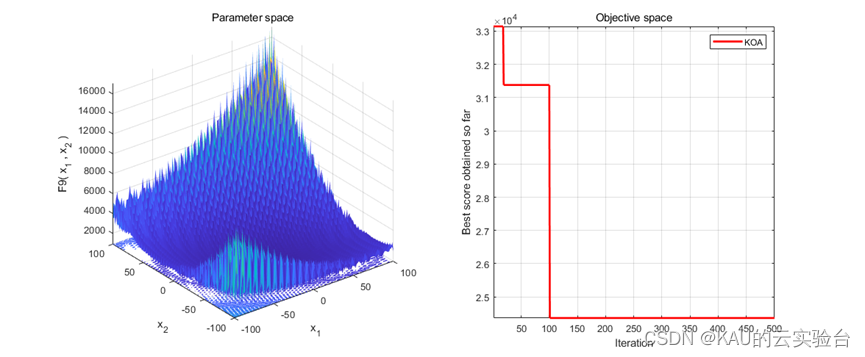
采用标准测试函数初步检验其寻优性能
在MATLAB中,进行CEC2017函数的测试,执行程序结果如下:
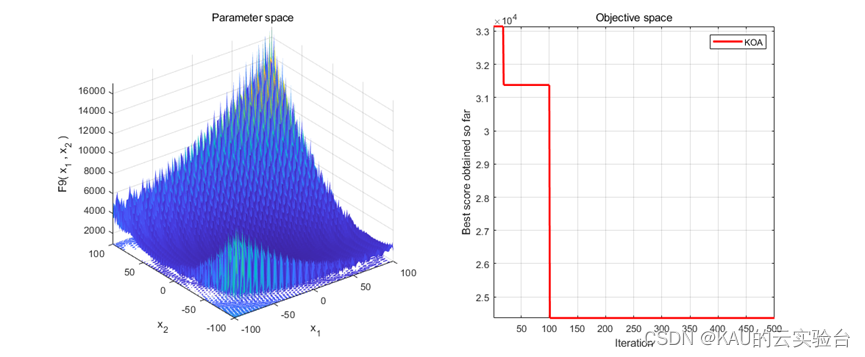
在Python中,进行CEC2005函数的测试,执行程序结果如下:
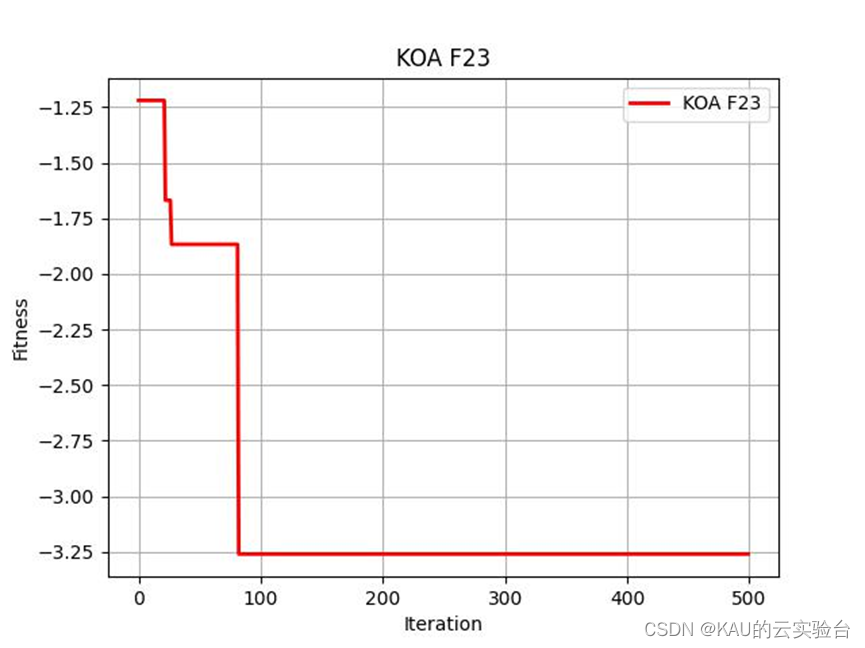
04 源码获取
在GZH(KAU的云实验台)后台回复 KOA 即可
参考文献
[1] Abdel-Basset, M. et al. Kepler optimization algorithm: A new metaheuristic algorithm inspired by Kepler’s laws of planetary motion. Knowl. Based Syst. 268, 110454 (2023).
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。