基本定义:
算法是一组有穷的规则,规定了解决某一特定类型问题的一系列运算。
关心算法的正确性和效率。
算法的五个重要特性:确定性、能行性、输入、输出、有穷性。
基础方法:
伪代码(Pseudocode):
例如:

个人觉得不需要过于追求伪代码的书写标准,不然反而失去了其意义。
循环不变式(Loop invariants)
定义:
在第一次进入循环之前成立、以后每次循环之后还成立的关系。
利用循环不变式证明算法正确性:
1)初始化:证明初始状态时循环不变式成立,即在循环开始之前为真;
2)保持:证明每次循环之后、下一次循环开始之前循环不变式仍为真;
3)终止:证明循环可以在有限次循环之后终止。
以插入排序为例:
1):在循环开始之前,j = 2,A[1 ~ j - 1]中仅A[1]一个元素,则A[1 ~ j - 1]有序成立。
2):每一次循环,在有序的A[1 ~ j - 1]中找到元素A[j]的位置k,将A[k + 1 ~ j - 1]的所有元素后移一位,并将原来的A[j]插入到A[k]的位置,A[1 ~ j]保持有序,此时原来的“A[1 ~ j]”变成了新的A[1 ~ j - 1]。
3):每次循环后 j 自增1,循环条件为 j < n ,因此 n - 1次循环后,循环必定结束。
算法分析
目的:预测算法需要资源(时间、空间)的程度。
算法的执行时间
:是运算i的执行次数,称为该运算的频率计数。
:是运算i在实际的计算机上每执行一次所用的时间。
仍以插入排序为例:

有:
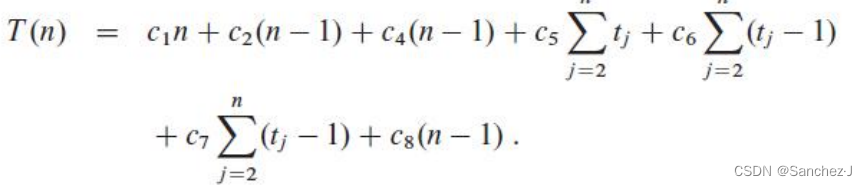
我们往往更关心最坏情况的执行时间
限界函数:
取自频率计数函数表达式中的最高次项, 并忽略常系数,记为:g(n)。