二叉树part08 235.二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点
235. 二叉搜索树的最近公共祖先
方法一:递归法(利用二叉搜索树性质)
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root==nullptr) return root;if(root->val > p->val && root->val >q->val) //左{TreeNode* left = lowestCommonAncestor(root->left,p,q);return left;}if(root->val < p->val && root->val < q->val) //右{TreeNode* right = lowestCommonAncestor(root->right,p,q);return right;}return root;}
};
方法二:迭代法(利用二叉搜索树性质)
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {while(root){if(root->val > p->val &&root->val > q->val) root = root->left;else if(root->val < p->val &&root->val < q->val) root = root->right;else return root;}return root;}
};
701. 二叉搜索树中的插入操作
方法一:递归找叶子节点
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr) {TreeNode* root = new TreeNode(val);return root; //找到叶节点,传给上一层递归}if(val < root->val) root->left = insertIntoBST(root->left,val); //向左遍历,接收叶子节点的数值else root->right = insertIntoBST(root->right,val);return root;}
};
方法二:递归找叶子节点,但通过全局变量记录parent位置
class Solution {
public:TreeNode* parent; //插入位置的父节点void traversal(TreeNode* cur, int val){if(cur==nullptr) {if(parent->val>val) parent->left = new TreeNode(val);else parent->right = new TreeNode(val);return;}parent = cur; //进入上一层前,提前保存叶子结点的父节点if(cur->val>val) traversal(cur->left,val);else traversal(cur->right,val);return;}TreeNode* insertIntoBST(TreeNode* root, int val) {if(root==nullptr) { //根节点为null的特殊处理root = new TreeNode(val);return root;}traversal(root, val);return root;}
};
方法三:迭代法
class Solution {
public:TreeNode* insertIntoBST(TreeNode* root, int val) {if (root == NULL) { //处理root为零特殊情况TreeNode* node = new TreeNode(val);return node;}TreeNode* cur = root;TreeNode* parent; // 这个很重要,需要记录上一个节点,否则无法赋值新节点while (cur != NULL) {parent = cur;if (cur->val > val) cur = cur->left;else cur = cur->right;}//找到parent位置了,接下来对parent的值和val对比,确定放在左节点还是右节点TreeNode* node = new TreeNode(val);if (val < parent->val) parent->left = node;// 此时是用parent节点的进行赋值else parent->right = node;return root;}
};
450. 删除二叉搜索树中的节点
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
第五种情况有点难以理解,看下面动画:
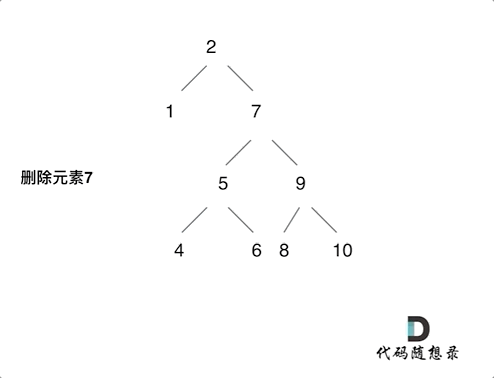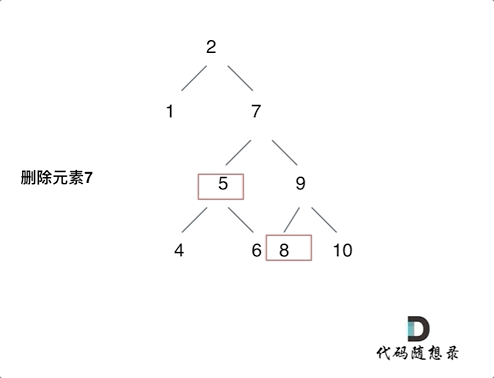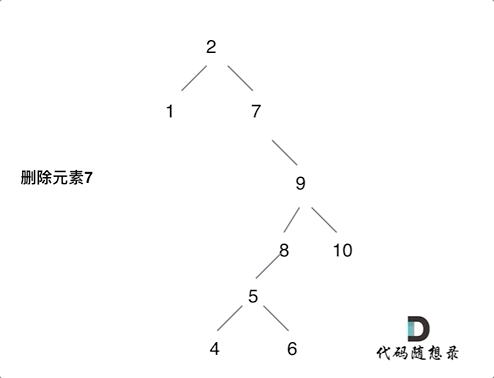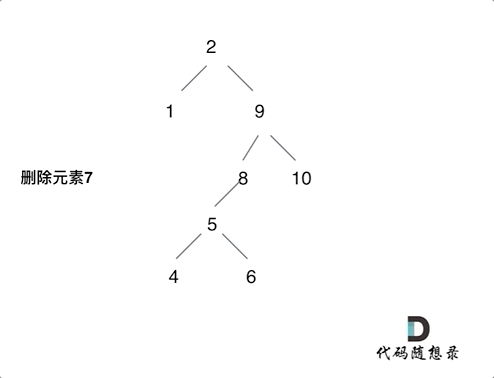
动画中的二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
将删除节点(元素7)的左孩子放到删除节点(元素7)的右子树的最左面节点(元素8)的左孩子上,就是把5为根节点的子树移到了8的左孩子的位置。
要删除的节点(元素7)的右孩子(元素9)为新的根节点。.
这样就完成删除元素7的逻辑,最好动手画一个图,尝试删除一个节点试试。
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int key) {if (root == nullptr) return root; // 第一种情况:没找到删除的节点,遍历到空节点直接返回了if (root->val == key) {// 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点if (root->left == nullptr && root->right == nullptr) {///! 内存释放delete root;return nullptr;}// 第三种情况:其左孩子为空,右孩子不为空,删除节点,右孩子补位 ,返回右孩子为根节点else if (root->left == nullptr) {auto retNode = root->right;///! 内存释放delete root;return retNode;}// 第四种情况:其右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点else if (root->right == nullptr) {auto retNode = root->left;///! 内存释放delete root;return retNode;}// 第五种情况:左右孩子节点都不为空,则将删除节点的左子树放到删除节点的右子树的最左面节点的左孩子的位置// 并返回删除节点右孩子为新的根节点。else {TreeNode* cur = root->right; // 找右子树最左面的节点while(cur->left != nullptr) {cur = cur->left;}cur->left = root->left; // 把要删除的节点(root)左子树放在cur的左孩子的位置TreeNode* tmp = root; // 把root节点保存一下,下面来删除root = root->right; // 返回旧root的右孩子作为新rootdelete tmp; // 释放节点内存(这里不写也可以,但C++最好手动释放一下吧)return root;}}if (root->val > key) root->left = deleteNode(root->left, key);if (root->val < key) root->right = deleteNode(root->right, key);return root;}
};

![[C#]C# OpenVINO部署yolov8实例分割模型](https://img-blog.csdnimg.cn/direct/48d6f935d195433dbf9570b92947a532.jpeg)