提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
前言
一、二叉树的存储结构
二、二叉树链式结构的实现
2.1手动构建一课树
2.2二叉树的遍历
三、二叉树链式结构的实现
3.1前序遍历(递归)
3.2中序遍历(递归)
3.3后序遍历(递归)
3.4层序遍历(非递归)
3.5求一棵二叉树节点的个数
3.6叶子节点的个数
3.7二叉树的高度
3.8求第k层的节点个数
3.9二叉树中查找值为x的节点
3.10通过前序遍历的数组构建二叉树("ABD##E#H##CF##G##",#是空)
3.11判断一棵树是否是完全二叉树
3.12销毁一棵树
四、二叉树的性质
总结
前言
世上有两种耀眼的光芒,一种是正在升起的太阳,一种是正在努力学习编程的你!一个爱学编程的人。各位看官,我衷心的希望这篇博客能对你们有所帮助,同时也希望各位看官能对我的文章给与点评,希望我们能够携手共同促进进步,在编程的道路上越走越远!
提示:以下是本篇文章正文内容,下面案例可供参考
一、二叉树的存储结构
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链,当前我们学习中一般都是二叉链,后面课程学到高阶数据结构如红黑树等会用到三叉链。

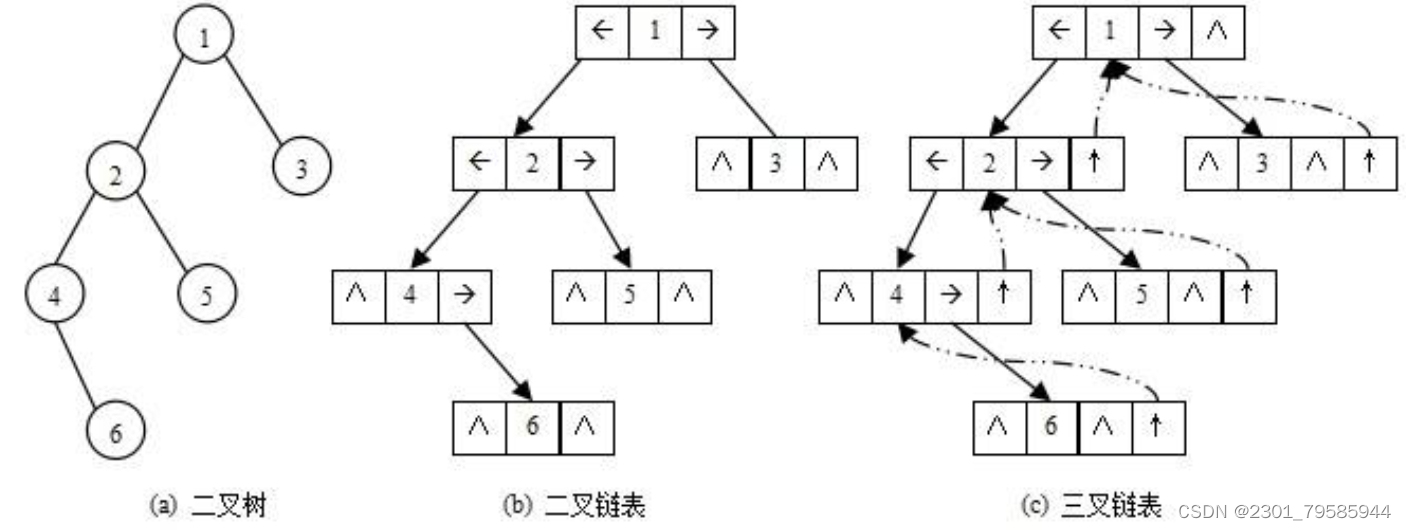
二、二叉树链式结构的实现
2.1手动构建一课树
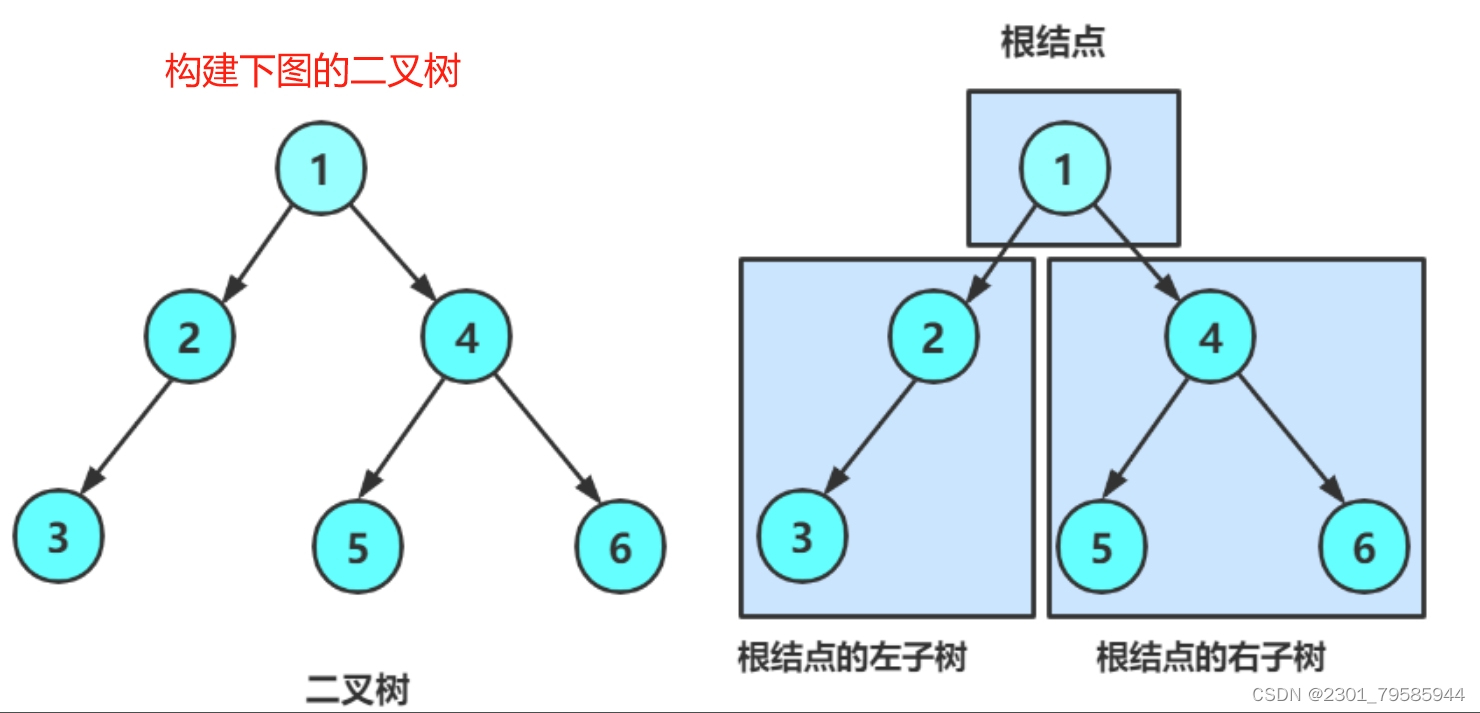
方法一:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}TreeNode;//手动构建一课树(方法一)
TreeNode* CreateTree()
{TreeNode* node1 = (TreeNode*)malloc(sizeof(TreeNode));assert(node1);TreeNode* node2 = (TreeNode*)malloc(sizeof(TreeNode));assert(node2);TreeNode* node3 = (TreeNode*)malloc(sizeof(TreeNode));assert(node3);TreeNode* node4 = (TreeNode*)malloc(sizeof(TreeNode));assert(node4);TreeNode* node5 = (TreeNode*)malloc(sizeof(TreeNode));assert(node5);TreeNode* node6 = (TreeNode*)malloc(sizeof(TreeNode));assert(node6);node1->data = 1;node2->data = 2;node3->data = 3;node4->data = 4;node5->data = 5;node6->data = 6;node1->left = node2;node1->right = node4;node2->left = node3;node2->right = NULL;node3->left = NULL;node3->right = NULL;node4->left = node5;node4->right = node6;node5->left = NULL;node5->right = NULL;node6->left = NULL;node6->right = NULL;return node1;
}方法二:
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}TreeNode;TreeNode* BuyTreeNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}//手动构建一课树(方法二)
TreeNode* CreateTree()
{TreeNode* node1 = BuyTreeNode(1);TreeNode* node2 = BuyTreeNode(2);TreeNode* node3 = BuyTreeNode(3);TreeNode* node4 = BuyTreeNode(4);TreeNode* node5 = BuyTreeNode(5);TreeNode* node6 = BuyTreeNode(6);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;
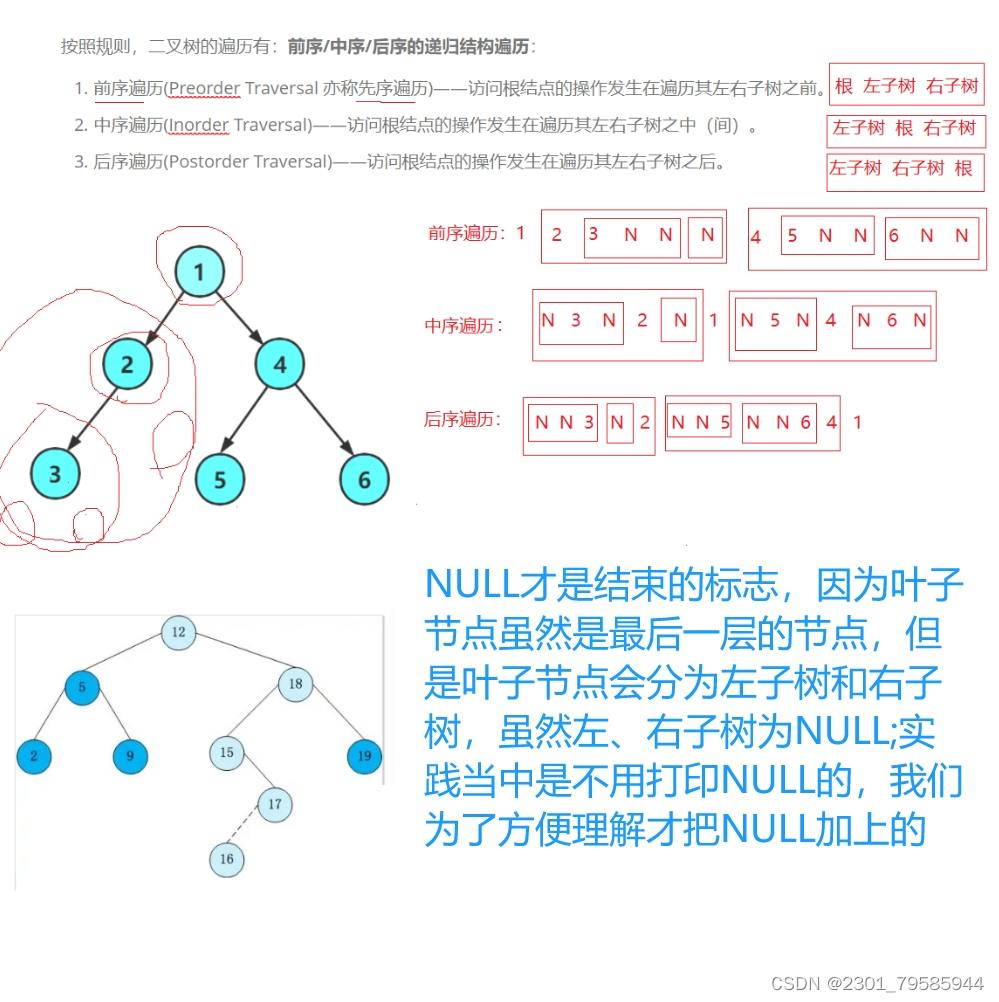
}2.2二叉树的遍历
前序遍历递归图解:
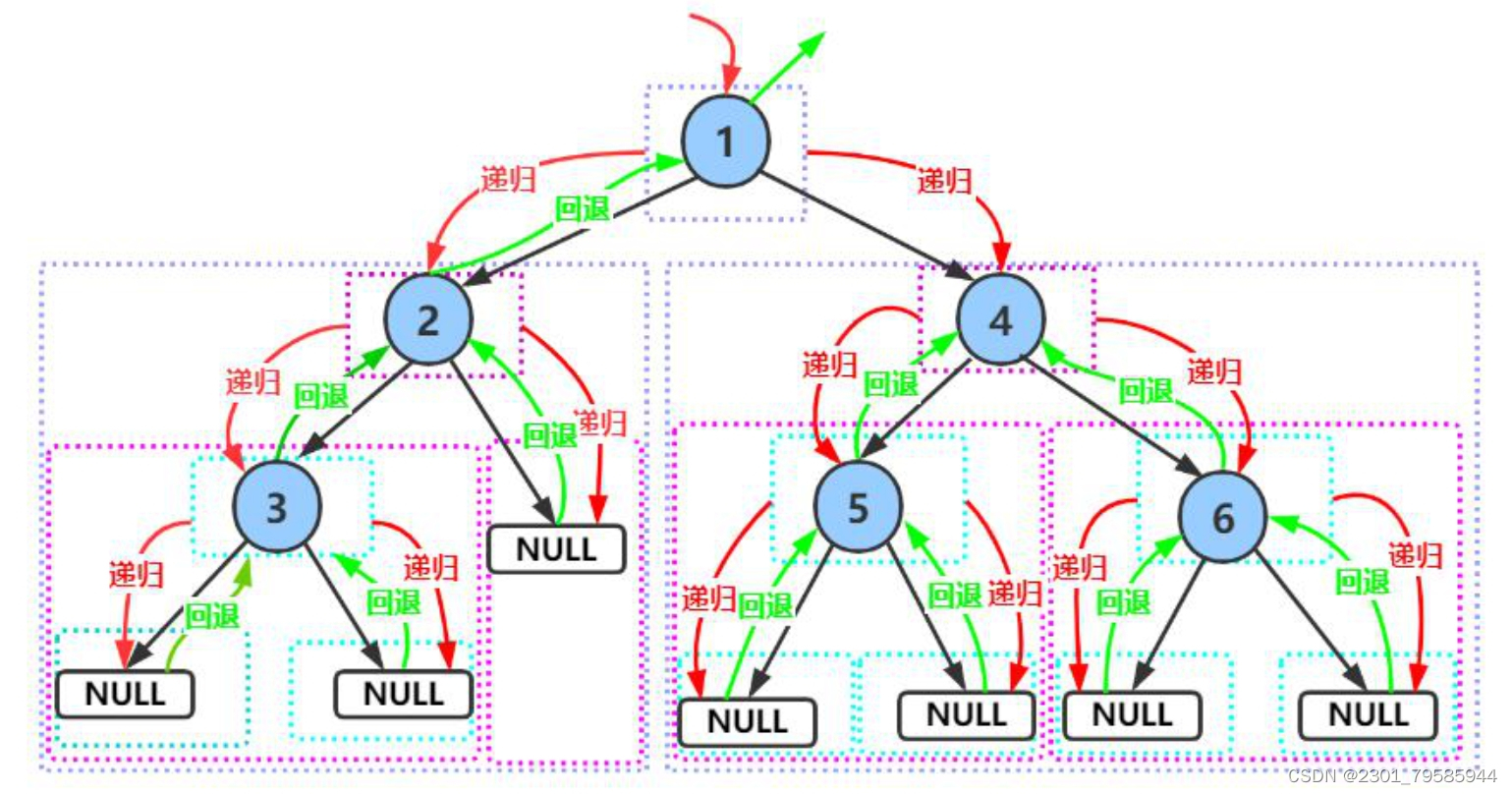
三、二叉树链式结构的实现
3.1前序遍历(递归)
//前序遍历(递归)
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

3.2中序遍历(递归)
//中序遍历(递归)
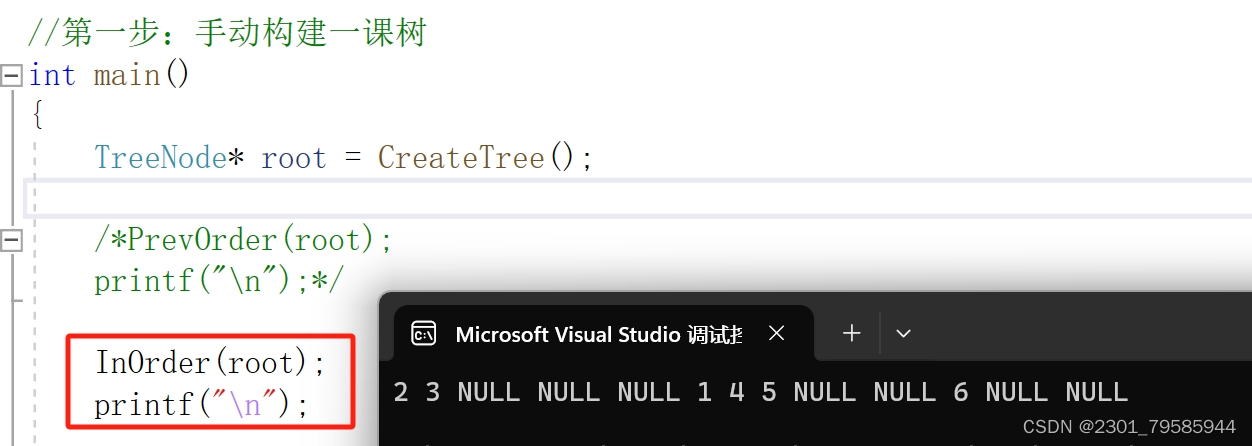
void InOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}PrevOrder(root->left);printf("%d ", root->data);PrevOrder(root->right);
}
3.3后序遍历(递归)
//后序遍历(递归)
void BackOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}BackOrder(root->left);BackOrder(root->right);printf("%d ", root->data);
}
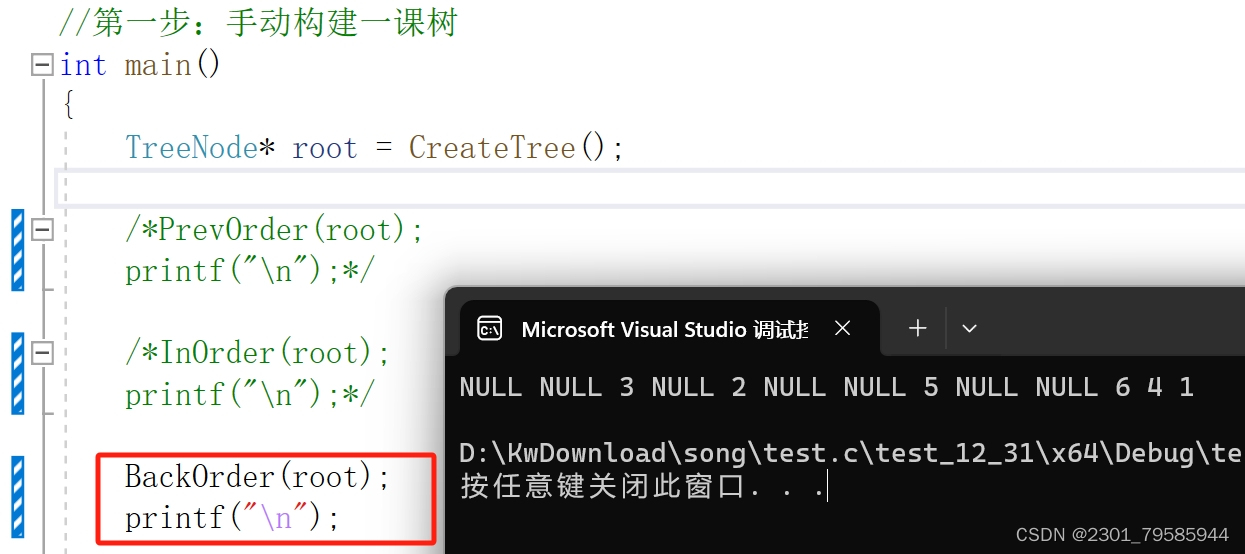
3.4层序遍历(非递归)
层序遍历(原理:上一层出来依次带入下一层),要利用队列先进先出的规则。

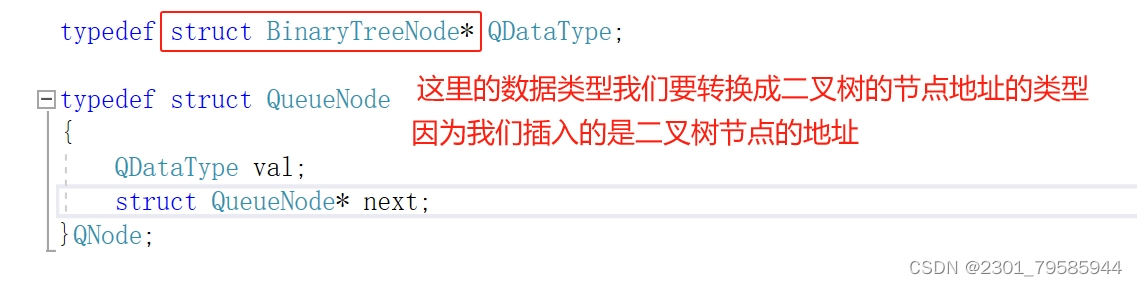
3.5求一棵二叉树节点的个数
方法一:
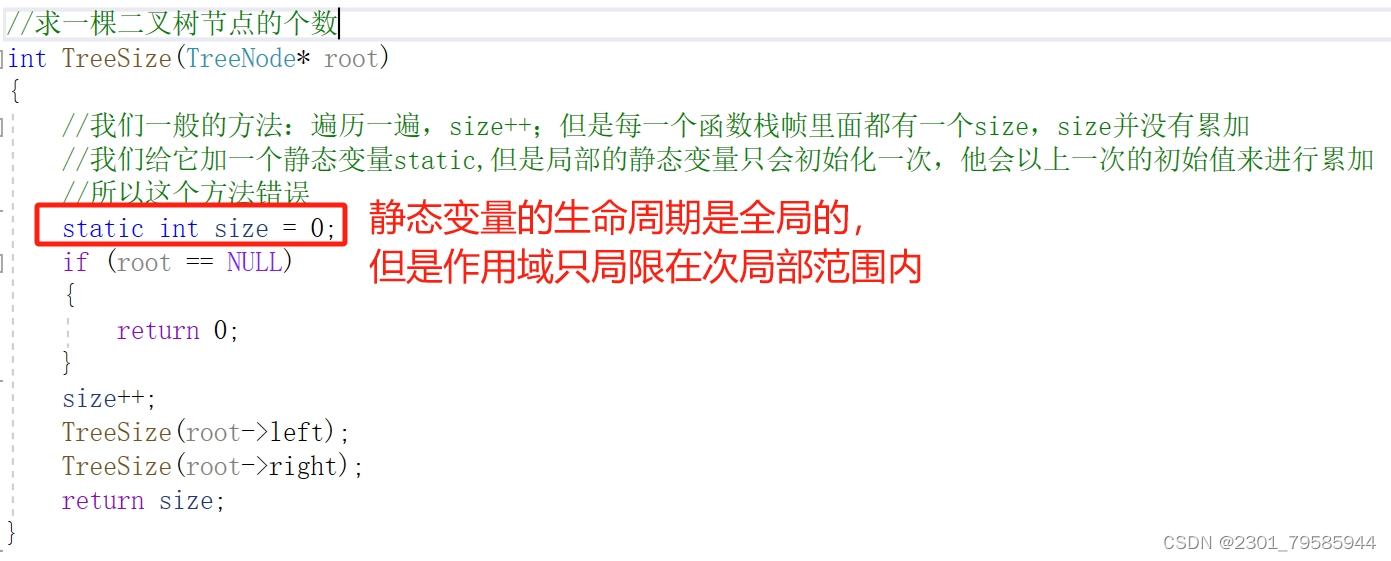

方法二:

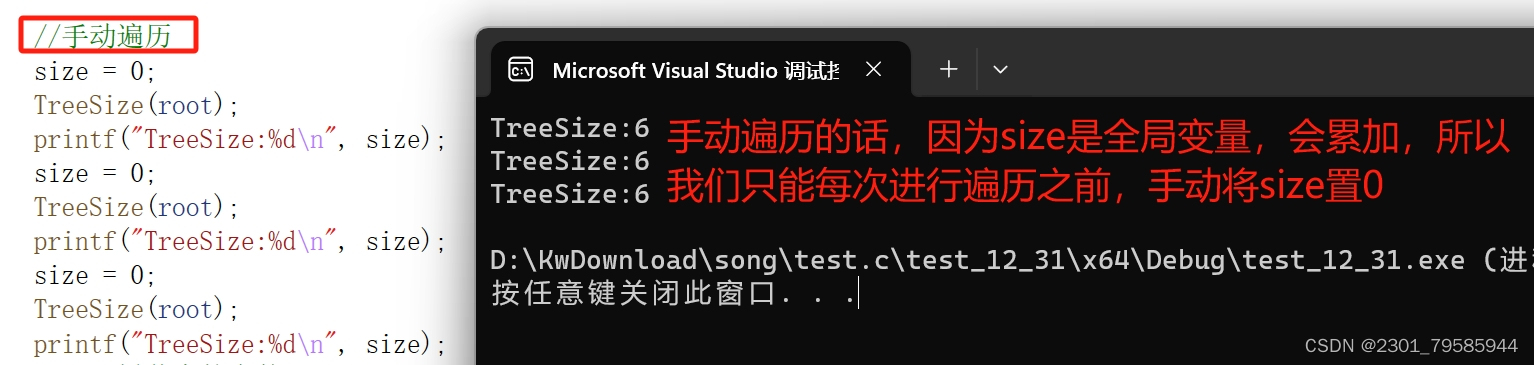
方法三:


3.6叶子节点的个数
//叶子节点的个数
int TreeLeafSize(TreeNode* root)
{//返回条件有两个//1、空 返回0if (root == NULL)return 0;//2、不是空,是叶子,返回1if (root->left == NULL && root->right == NULL)return 1;//不是空,也不是叶子,分治=左右子树叶子之和return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

3.7二叉树的高度
方法一:
//求二叉树的高度
int TreeHeight(TreeNode* root)
{//空树,返回0if (root == NULL)return 0;//不是空树,左子树高度与右子树高度比较,大的高度+1//记录一下左右子树的高度int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}方法二:
//求二叉树的高度
int TreeHeight(TreeNode* root)
{//空树,返回0if (root == NULL)return 0;//不是空树,左子树高度与右子树高度比较,大的高度+1//记录一下左右子树的高度(fmax:C语言的库函数)return fmax(TreeHeight(root->left),TreeHeight(root->right))+1;
}
3.8求第k层的节点个数


3.9二叉树中查找值为x的节点
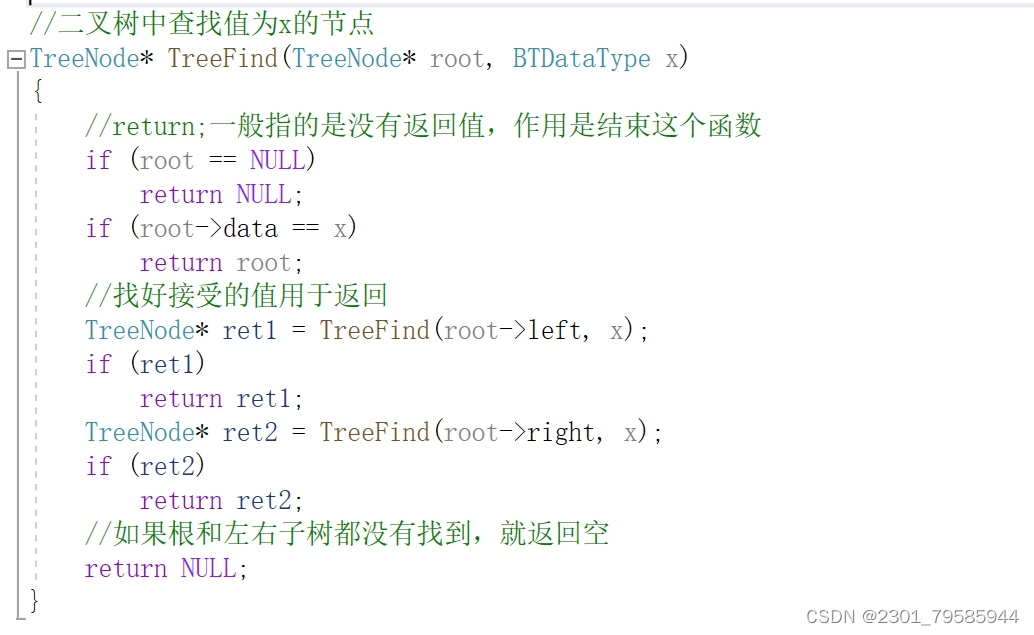

3.10通过前序遍历的数组构建二叉树("ABD##E#H##CF##G##",#是空)
// 通过前序遍历的数组构建二叉树("ABD##E#H##CF##G##",#是空)
TreeNode* TreeCreate(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = a[(*pi)++];root->left = TreeCreate(a, pi);root->right = TreeCreate(a, pi);return root;
}
3.11判断一棵树是否是完全二叉树
//判断一棵树是否是完全二叉树
bool TreeComplete(TreeNode* root)
{//队列内要放的是节点,因为我们还要节点的左右孩子Queue q;QueueInit(&q);if (root)QueuePush(&q, root);//push的是一个节点的指针,也就是push的是节点里面的一个值while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}//前面的遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}
3.12销毁一棵树


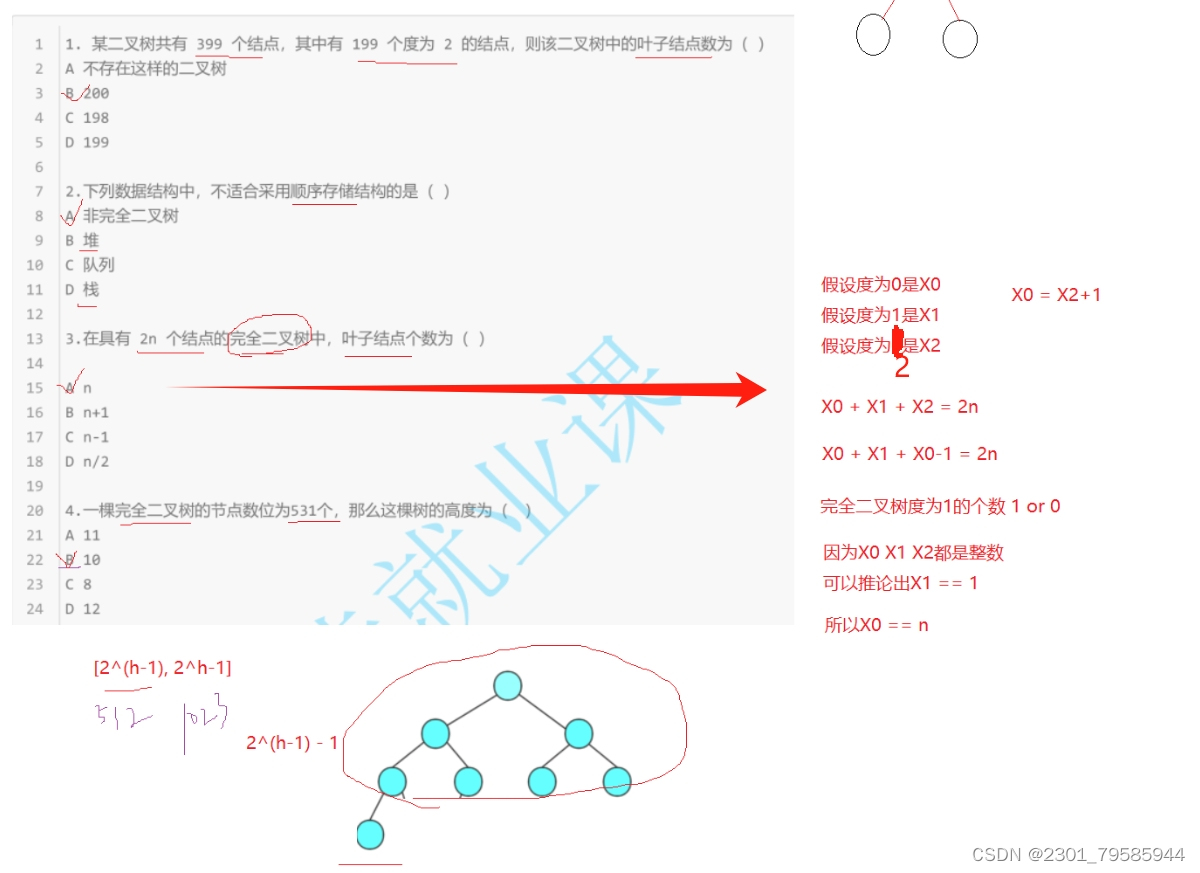
四、二叉树的性质
节点的度:一个节点含有的子树的个数称为该节点的度。
树的度:一棵树中,最大的节点的度称为树的度。

总结
好了,本篇博客到这里就结束了,如果有更好的观点,请及时留言,我会认真观看并学习。
不积硅步,无以至千里;不积小流,无以成江海。